開發校本教材 提升學生的數學思維能力

付 穎

（福建省福州市烏山小學）

數學思想是指人們對數學知識內容和所使用方法的本質認識，它是從某些數學認識過程中提煉和概括出來后被反復證實的數學規律。數學方法是數學思想的表現形式和得以實現的手段。掌握了數學思想方法，在一定意義上來說就是掌握了數學的精髓。數學思想方法也是增強學生數學觀念，形成良好思維能力的關鍵要素之一。因此，在數學課堂教學中應該注重數學思想的滲透，要通過各種方式展示數學思想方法，提高學生的數學思維能力。

一、從實際問題出發，明確挖掘校本思維教材的必要性

數學思想在我國數學課程目標的發展中經歷了從無到有的變化。《義務教育數學課程標準(2011年版)》中提出：“數學課程不僅包括學習數學的結果，也包括數學結果的形成過程和其中所蘊涵的數學思想方法。”同時，《義務教育教學課程標準（2011年版）》也不斷強調要重視在教學中滲透數學思想方法。而在實際課堂中，對數學思想培養的落實情況如何呢？

在人教版《義務教育教科書·數學》一年級下冊第二單元“20以內的退位減法”的教學結束后，我們對學生計算方法多樣化的掌握情況進行了調查，題目是“請用多種方法計算14-6”。絕大多數學生都能正確地寫出計算結果，但有三分之一以上的學生寫不出思考過程。而此題除教材中出現的2種方法（想加做減、破十法）之外，還有5種不同的方法：連減法、多減再加、多加再減、同加法、同減法，就因為教材中沒出現、教師不關注，因此沒有幾個學生能夠寫出教材所示之外的第三種方法。

這項測試反映了教師和學生缺乏對數學思想的關注，教材中已有的鍛煉數學思維的機會都不夠重視，教材中沒出現的就更可想而知了。這樣不僅限制了學生數學思維的發展，也抑制了學生創造性的發揮。面對如此的教學現狀，我校負責第一學段教學的教師率先嘗試，群策群力，通過深入挖掘教材，一起開發了校本思維教材。

二、以學生發展為本，找準思維教材的定位

在開發教材的初期，我校很多教師都想要借助市場上的奧數思維培訓教材，選取適用的部分作為校本思維教材的藍本。可是，通過仔細閱讀，我們發現，奧數思維培訓教材起點較高，并不適用于學習程度中等及以下的學生。結合我校“樂思、善思”的辦學理念，若強行引入教學，不但不能培養學生學習數學的興趣，反而會適得其反。為此，我們再次翻開了數學教材，通過對數學教材的再度研究，我們得出了新的思路，那就是校本思維教材不應是高深莫測的，而應像數學教材那樣既能夠讓學生看得懂，又有濃厚的鉆研興趣。最關鍵的是，要能滲透數學思想方法，提升思維能力，即校本思維教材應立足于教材，在思維開發程度上又略高于教材。

關于校本思維教材的編排形式我們也進行了定位，校本思維教材需要為學生創設輕松活潑的學習氛圍。首先，我們確定了校本思維教材的主人公：兩個漫畫卡通形象阿U和阿美；其次，在編寫上采用兩個動漫形象對話的形式輕松展開教學；最后，基于第一學段的年齡特征，校本思維教材的內容呈現采用數形結合的方式。

三、以課內教材為本，設計多種類型的校本思維教材

在對教材進行較為深入地鉆研和發掘的基礎上，我們歸納了適合做校本思維教材內容的三種類型。

（一）新知的拓展延伸

數學校本思維教材可以是對課內知識的拓展。

一類是對新授課例題的拓展。我們深入挖掘新授課中能有效拓展學生數學思維能力的課例，將之賦予豐富的數學思維方法，編寫入我們的校本思維教材。

如我們將“9的乘法口訣”這節新授課設計為校本思維教材“找9的乘法口訣規律”。以往的課堂中，教學目標是通過發現規律熟悉9的口訣，而我們借助9的乘法口訣來培養學生的觀察能力，做了極大的創新。學生在前面已學過1到8的乘法口訣，他們極為熟悉口訣的形成和含義，因此完全具備獨立學習9的口訣的能力。9的口訣中有許多規律，這些規律有些是顯性的，有些是隱性的，而其中隱性的規律對學生的觀察能力提出了極大的挑戰，這些規律的發現不僅對記憶9的口訣這個知識性目標有很大的作用，而且其中著蘊含數形結合思想、優化思想等多種思想方法。在觀察活動中，學生可以積累經驗，提升數學思維能力。

另一類是新授課后的拓展延伸。新授課學習之后，根據教學內容設計有針對性的思維拓展題，不僅能促進學生對課內知識的掌握，還能提升學生綜合運用的能力，使學生獲得最大程度的發展。

如在學習了人教版《義務教育教科書·數學》一年級下冊“找規律”之后，我們設計了“創造規律”這一校本思維教材。（如圖1）此校本思維教材的設計，不僅幫助學生復習了課堂中的各種不同規律，還有效溝通了圖形之間的規律和數之間的的規律，滲透了數形結合的思想，并且激發了學生挑戰自我的熱情，培養了創新意識。

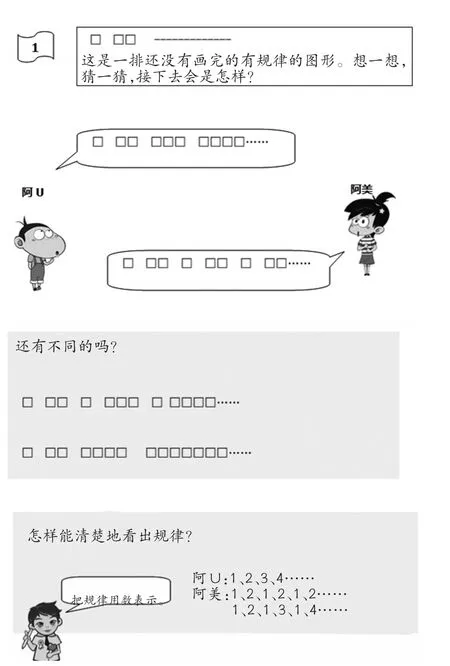
圖1

（二）練習的拓展延伸

數學校本思維教材也可以是對課內某一道或某一類練習的拓展。數學教材中有些拓展性的練習設計得很好，而且這些題目中都蘊涵有豐富的數學思想方法。如果只作為一道練習題讓學生花少量的時間去訓練，不僅學生難以掌握，而且只是就題論題，實則可惜。為此，我們將其拓展，變成了數學校本思維教材。這一類的教材編寫，從新課到練習編寫都是一次極具創新性的原創設計。

這節課我們的教學目的絕不是解決這類排隊問題，而是不斷讓學生自己嘗試通過畫圖解決問題，滲透了數形結合和符號化思想。

（三）“數學廣角”或綜合實踐的拓展延伸

數學校本思維教材可以選材于部分綜合實踐活動課程。這是人教版教材中新增設的一個內容。以往的課堂上，很多教師要么略過不教，要么僅僅是簡單的介紹。但若是仔細研讀教材，我們就會發現：這些綜合實踐課程，往往都是對一個單元所學知識的提煉，具有很強的探究性，對于學生增強應用數學的意識，提高數學思維能力、實踐能力和解決問題的能力是很有幫助的。這些課程足以讓學生深切體會數學的應用價值及趣味性，提升學生的數學思維能力。如果把這樣的內容專門進行一定的改編，就會使是非常好的數學校本思維教材。

圖2

圖3

圖4

教材中的“數學廣角”也可以開發為數學校本思維教材，但必須是對教材中的內容有更為深刻的思考，對教材進行不同角度的改編。如人教版《義務教育教科書·數學》三年級下冊的“搭配”一課，很多教師在教學時所想到的都是要滲透教參中提到的“有序思考、符號化思想”。但我們發現，用這種方式教學，當在看似難度并不大的變式題出現時，大多數學生都會認為這道變式題并不屬于搭配問題，并且學生會呈現茫然、不會解答的狀態。經過不斷實踐探究，我們終于取得了一定的突破，有了新的發現：原來我們忽視了“建模思想”在其中的重要作用，于是我們就把這一課改編成了我們的數學校本思維教材（如圖2至圖7所示）。

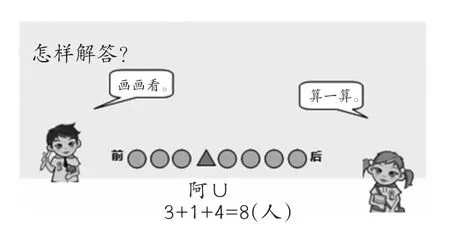
圖5

圖6

圖7