法蘭連接的轉子剛度損失特性研究

喬磊 張康 趙丹

摘? 要：航空發動機轉子在連接處的剛度損失探究，對發動機轉子的動力學特性分析及發動機總體設計具有重要支撐作用。本文首先通過ANSYS Workbench對有限接觸面的接觸剛度進行仿真計算，結合理論分析了接觸剛度非線性的原因。然后定義了應力分布系數（SDF），對不同法蘭結構參數下的轉子彎曲剛度進行有限元分析，得到了不同結構參數下SDF和轉子彎曲剛度的關系曲線，為法蘭連接的工程設計提供了理論參考依據。

關鍵詞：法蘭連接;彎曲剛度;應力分布系數

中圖分類號：TH113.1? ? 文獻標識碼：A ? ? ? 文章編號：1671-2064（2020）03-0000-00

1 研究背景

在螺栓連接的法向剛度研究上，國內外大部分學者[1]普遍支持的觀點是法蘭厚度，螺栓數量，扭緊力矩[2]會從不同方面對安裝邊應力分布產生影響。

Gould等[3]用面載荷模擬螺母對安裝邊預緊力，分析了安裝邊壓緊區域內壓應力分布的非線性關系。Ziada等[4]運用有限元方法對螺栓連接結構建立其完整的3D模型，研究了不同尺寸螺栓下的應力分布規律。尤晉閩等[5]運用分形接觸理論構建了法蘭連接結構結合面的接觸模型，其研究認為法蘭結合面只有一小部分面積參與了真實接觸。Marshall等[6]對螺栓壓緊的法蘭安裝邊進行超聲掃描測量。得到不同壓緊力作用下法蘭安裝邊的影像，進而分析了接觸面的壓力分布與實際接觸面積。上述對法蘭連接的剛度研究忽視了慮螺栓頭壓緊下的法蘭變形，未將應力分布與法蘭連接剛度進行關聯分析。

2 法向剛度與彎曲剛度

假設法蘭接觸面在螺栓預緊下單位面積的法向剛度為K_T，取成對微元段d_θ進行分析，如圖1。

圖1所示微元對繞x軸的抗彎剛度為：

連接結構處對繞x軸的抗彎剛度K_w為：

由式（2）可見法蘭接觸剛度直接決定了連接結構處的抗彎剛度。

3 接觸平面受集中力的法向剛度

螺栓頭在壓緊法蘭邊后的變形如圖2所示，實際變形出現應力分布不均勻的情況，造成了接觸剛度與載荷的非線性關系。

3.1 理論及公式分析

假設半無限體受有限均布載荷F，距載荷中心無限遠L處的變形為零，載荷作用面積為G，則微元面k處的載荷為dF=dlF/G。令G的中心與點m的距離為x，積分的點m處的位移為：

無量綱剛度K=F/lnF，可以看出有限面載荷與接觸面的法向剛度是非線性關系。

3.2 有限元建模分析

建立有限元計算模型如圖3，該模型的尺寸參數已標于圖3中，取模型中兩物體材料均為GH4169，其彈性模量E=204GPa，泊松比ν=0.30，密度ρ=8240Kg/m3。

施加向載荷大小為10kN～60kN，通過有限元計算其無量綱法向剛度。將有限元計算結果與理論計算結果列于圖4。

從圖4中可以看出法向剛度與載荷的非線性關系明顯，且理論計算與有限元分析結果具有較好一致性。理論計算的剛度稍強于有限元分析的結果，造成這種現象的原因是理論推導假設受力面變形是相等的平面，如圖5（a），而有限元分析的實際變形是空間連續曲面，所以中心點位移較大，使理論剛度計算較小。

4 法蘭連接剛度有限元計算

4.1 法蘭連接剛度有限元模型的建立

建立法蘭連接的有限元分析模型如圖6，其相關材料物性參數與上一節相同，采用M6的螺栓對法蘭進行連接，連接螺栓數為18，為該尺寸模型許用的最大螺栓數。

4.2 不同螺栓數下的彎曲剛度

取螺栓預緊力F_prelod=8kN，計算不同螺栓數下該模型的彎曲剛度，結果見圖7。

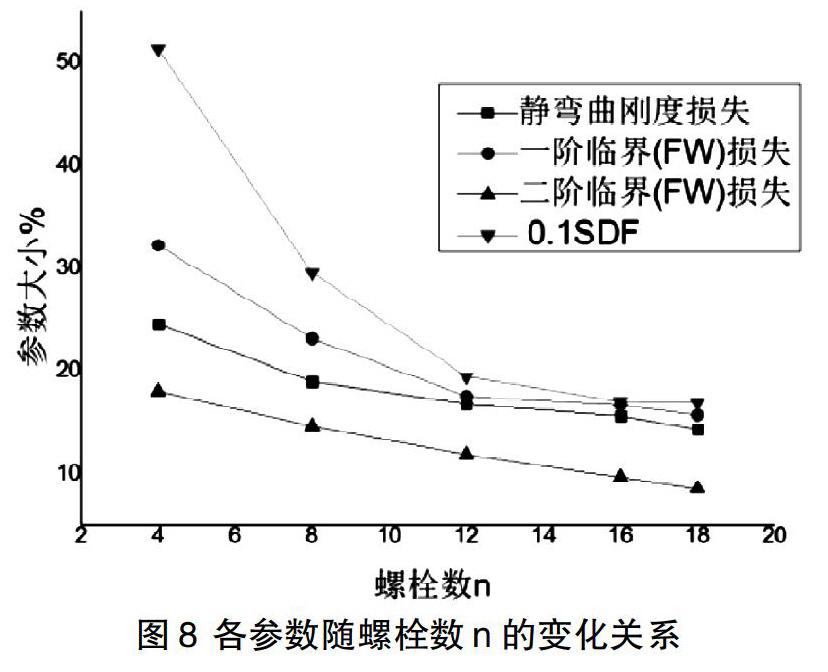
計算在不同螺栓數下該模型的靜彎曲剛度與臨界轉速損失，將結果列于圖8中。

從圖8的結果中可以看出，隨著螺栓數n的增加，法蘭連接剛度不斷提升。在螺栓數較少時，剛度提升明顯，隨著螺栓數增多，連接剛度提升微弱且相對于固接始終存在較大損失。在本文的計算模型下，D螺栓公稱直徑，當螺栓孔間距t=2.16（n=12）以后，增加螺栓數不能明顯提高法蘭連接剛度。

螺栓數n為8，12，16下的法蘭面的法向應力見圖9。

其中，S_max為接觸面上的最大應力，S_min為接觸面上的最小應力，S_c為平均應力。計算不同螺栓數下法蘭面的SDF于表1。

以上數據可看出，隨著連接螺栓數增加，法蘭面的應力分布均勻程度度在改善，在螺栓數較小時改善速率較快，在螺栓數增加到一定程度時，改善比較緩慢，這一規律和彎曲剛度與螺栓數的關系高度吻合，說明螺栓數的增加使應力分布改善從而增加了連接剛度。

4.3 不同預緊力下的彎曲剛度

本節以上一節的分析模型和材料條件，通過有限元計算在螺栓數n=12時，不同螺栓預緊力下模型的彎曲剛度。取F_prelod=4kN，6kN，12kN下的安裝邊應力云圖見圖10。不同預緊力下接觸面的SDF見表2。

從圖10及表2中可以看出，在相同的螺栓數下增加螺栓預緊力并不能明顯改變法蘭接觸面的應力分布水平。

在螺栓預緊力為4kN～12kN下的連接結構彎曲剛度如表3所示。

由表3數據可得，隨著螺栓螺栓預緊力的增加，連接剛度的提升并不明顯，這與增加預緊力不能明顯改善應力分布水平的結論一致。

5 結論

本文基于ANSYS Workbench有限元建立了典型的法蘭連接轉子模型，計算了不同連接參數下的彎曲剛度，定義了法蘭面的應力分布系數SDF，結合理論推導，分析證明改善法蘭面應力分布均勻程度能有效減少連接處的剛度損失。

在法蘭連接結構設計中，應盡可能選用使法蘭面應力分布均勻性較好的方案以獲得較少的連接剛度損失。

在保證安裝邊緊密連接后，增加螺栓預緊力并不能明顯提升連接剛度，所以在抵抗軸向力載荷及預留密封應力之后，法蘭連接的剩余預緊力不宜設計得過大。

參考文獻

Fernlund，I.A method to calculate the pressure between bolted or riveted plates[J].Transactions of Chalmers University of Technology，1961（245）.

姚星宇，王建軍.航空發動機螺栓連接載荷與結構參數對連接剛度影響規律[J].推進技術，2017，38（2）：424-433.

Gould H H，Mikic B B.Areas of contact pressure distribution in bolted joints[J].Journal of Manufacturing Science and Engineering，1972，94（3）：864-870.

Ziada H H，Abd El Latyif A K.Loading conditions in bolted and riveted joints affected by plate thickness ratio[J]. Journal of Mechanical Design，1980，102（4）：93-100.

尤晉閩，陳天寧.結合面法向動態參數的分形模型[J].西安交通大學學報，2009，43（9）：91-94.

Marshall M B，Lewis R，Dwyer-Joyce R S Characterisation of contact pressure distribution in bolted joints[J].Strain，2006，42（1）：31-43.

收稿日期：2020-01-04

作者簡介：喬磊（1994—），男，四川成都人，碩士研究生，助理工程師，研究方向：航空宇航推進理論與工程。