船舶主動減振器安裝位置選取和設備選型

呂志慶，黃金林，高占峰

（中遠海運重工有限公司設計研究院，遼寧大連 116024）

0 引言

船體梁振動是船舶振動形式中危害最大、最難解決一種。船體梁振動不僅帶動生活區的晃動，還影響了船員與乘客的舒適度，甚至可能影響船舶的疲勞壽命，威脅到船舶的安全。尤其低階船體梁振動，頻率低、振幅大，該振動形式的出現表明該船沿船長方向的剛度設計與主機選型不匹配。局部的結構形式修改和重量布置調整對船體梁振動幾乎無效，只有通過減小振源的方式才能有效的降低該振動產生的危害。

主機垂向不平衡力矩是引起船體梁振動的一種常見激勵，如圖1所示。通常，MAN的主機可以通過在主機前后兩端安裝偏心輪的方式（常作為主機合同中的備選項）抵消該力矩，而瓦錫蘭主機多數無法安裝偏心輪，需要外接主動減振器。通過主動減振器產生一個與主機不平衡力矩頻率相同的力，以抵消主機不平衡力矩的影響。

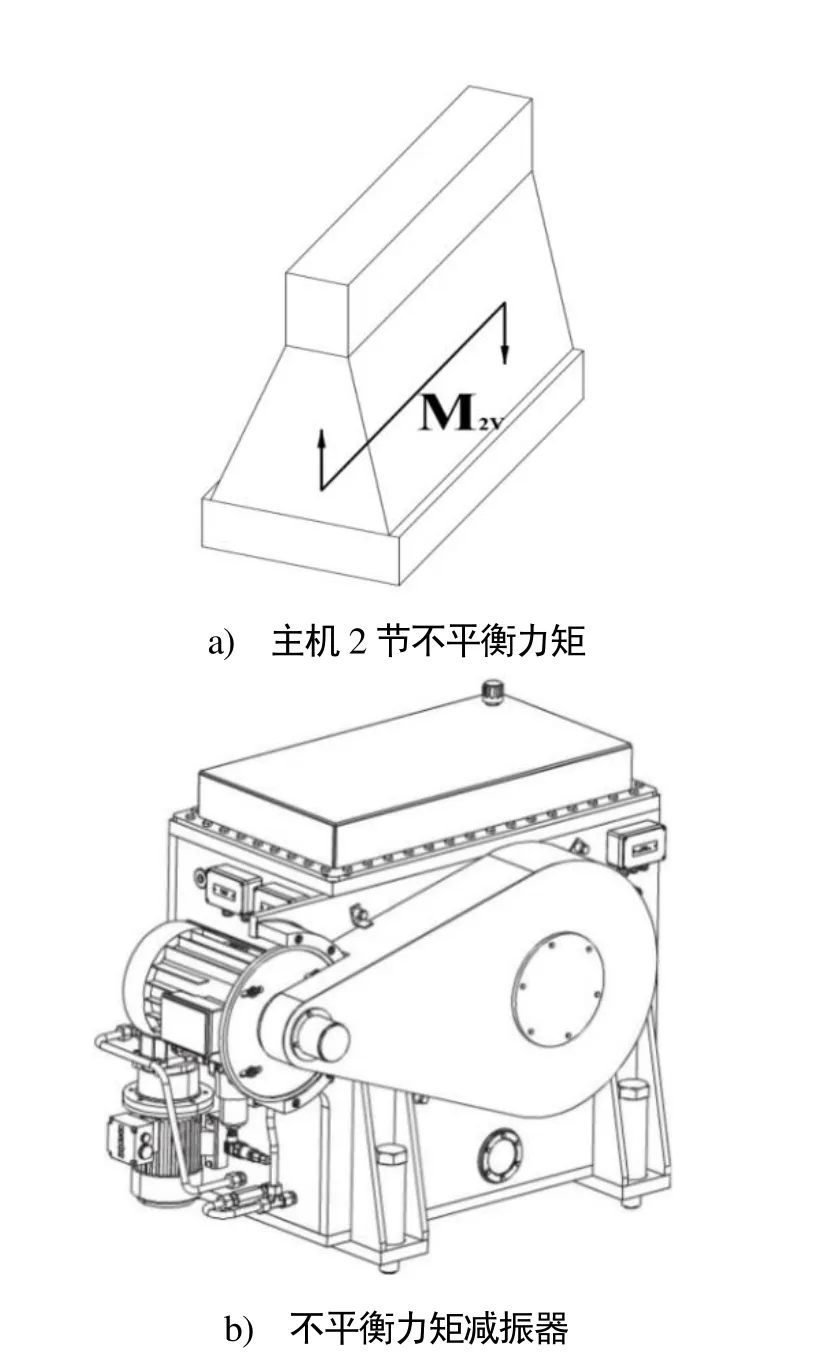
圖1 主機2階垂向不平衡力矩和不平衡力矩減振器

本文從船體梁受迫振動的機理出發，推導船體梁振動發生的理論依據，并探索振動對外界激勵位置的敏感程度，進而得出一系列關于減振器安裝位置、選型和減振效果的結論，并采用有限元法進行驗證，最后在某集裝箱實船項目中進行驗證。

1 伯努利梁受迫橫向振動機理研究

1.1 伯努利梁受迫振動求解

忽略阻尼影響，伯努利梁彎曲振動的運動方程為[1-2]

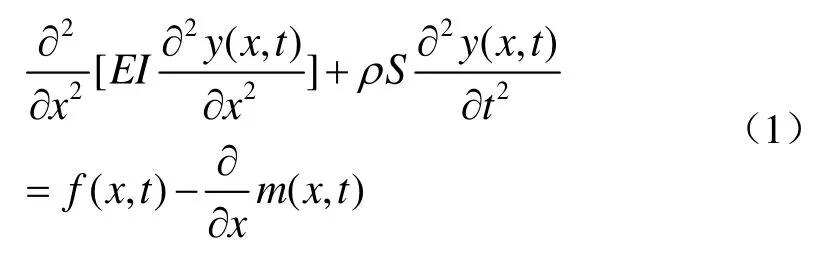
式中：f(x,t)為外界作用力；m(x,t)為外界作用力矩。

采用分離變量法，方程解的形式為

式中：φ(x)為梁的振型；q(t)為隨時間變化的振幅。

已知伯努利梁的自由振動固有頻率和振型，采用模態疊加法計算梁受迫振動方程（1）的解。令

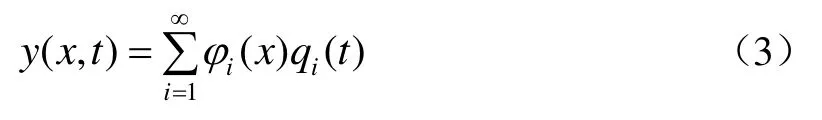
將式（3）代入式（1）可得

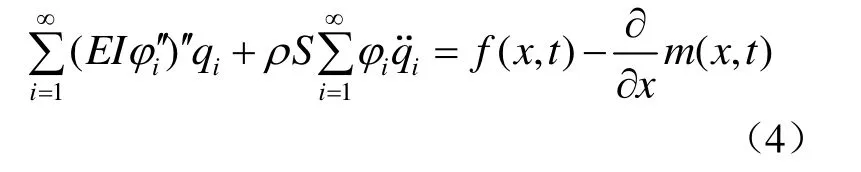
方程（4）兩邊乘φj并沿梁長對x積分得

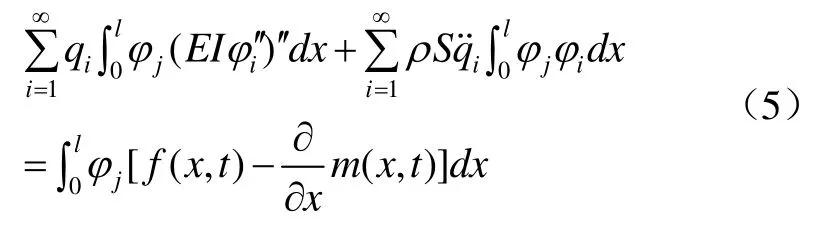
根據模態函數的正交性，上式可轉化為

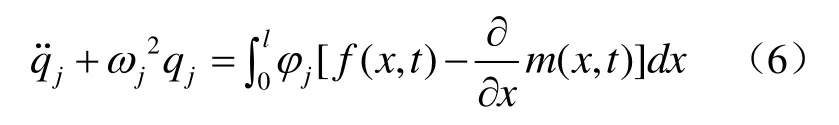
根據分部積分

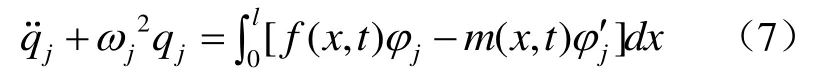
假設伯努利梁在x=x1處受集中力F(t)，在x=x2處受集中彎矩M(t)，此時上式可用δ函數表示為分布形式

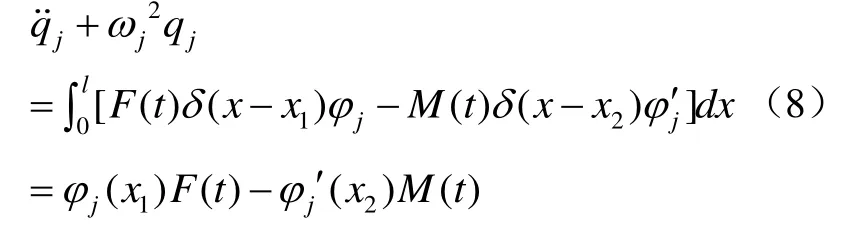
對公式（8）采用杜哈梅爾積分[3,4]

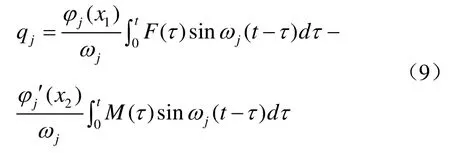
將式（9）帶入式（3）得最終響應為

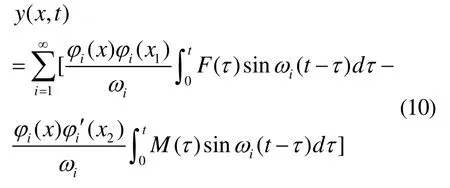
1.2 受迫振動響應分析

式（10）即為伯努利梁受迫振動的振動響應表達式，其中第一項為某點受集中力作用的響應，第二項為某點受集中力矩作用的響應。對式（10）進行分析

1）若伯努利梁僅在x=x1處受動態集中力作用，且外力的激振頻率與第j階固有頻率相等，即發生共振，根據模態正交性原則，將式（10）轉化為

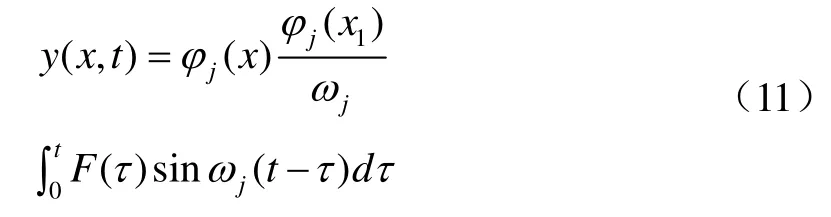
式中：φi(x)、ωi均為梁的固有屬性，當激振力幅值和激振頻率確定時，振動響應值僅取決于φi(x1)的值，即激振力在梁上的作用位置x1。由式（11）可知，當激振力作用于模態φi(x)的節點時，φi(x1)=0，振動無法被激起；當激振力作用于模態φi(x)的波腹時，φi(x1)最大，此時振動響應最大。

2）若伯努利梁僅在x=x2處受動態集中彎矩作用，且外力矩的激振頻率與第j階固有頻率相等，即發生共振，根據模態正交性原則，將式（10）轉化為

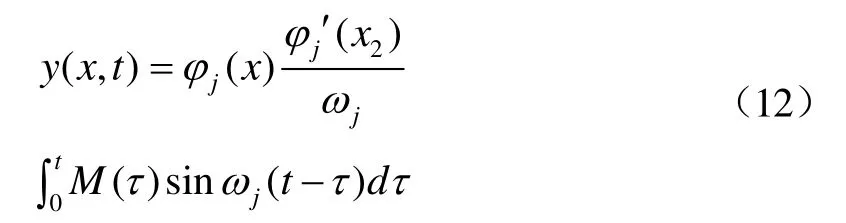
同理，振動響應值僅取決于φi'(x2)的值，即該梁第j階振型在點x2處的斜率，最終取決于激振彎矩在梁上的作用位置x2。由式（12）可知，當彎矩作用于模態φi(x)的波腹時，φi'(x2)=0，振動無法被激起；當彎矩作用于模態φi(x)的節點時，φi(x2)最大，此時振動響應最大。

3）若伯努利梁在x=x1處受到動態集中力作用，同時在x=x2處受集中彎矩的作用，如圖2所示，且力和彎矩的頻率相等（均與第j階固有頻率相等），根據模態正交性原則，可將式（10）轉化為

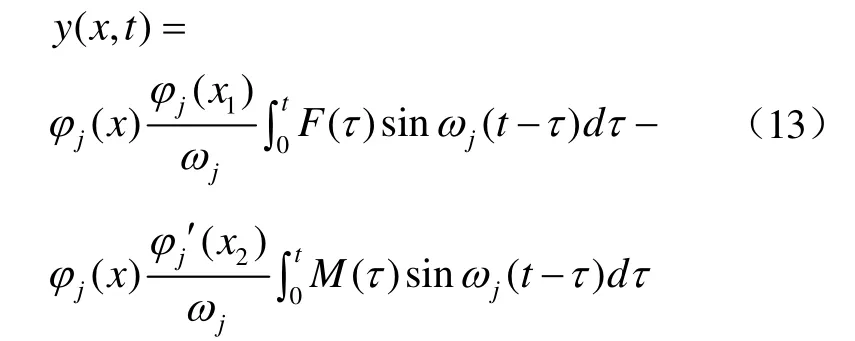
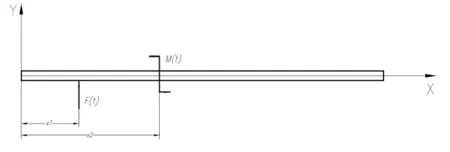
圖2 伯努利梁同時受集中力和集中力矩

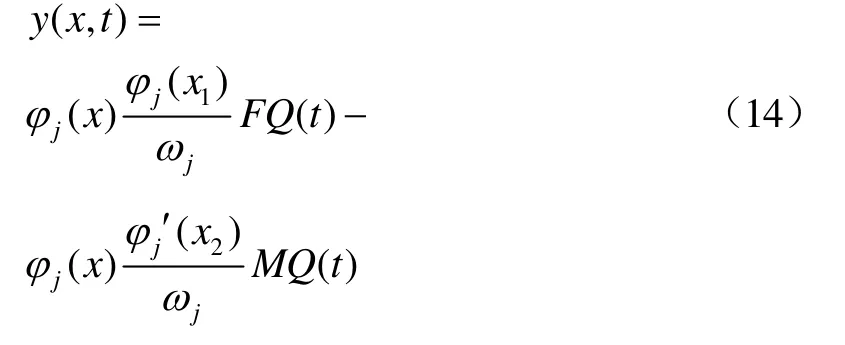
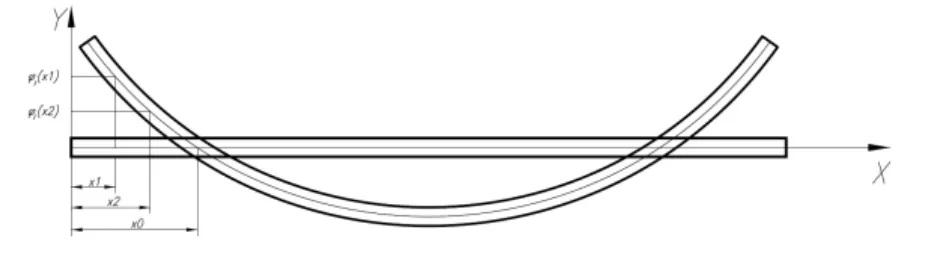
圖3 自由伯努利梁一階振型

圖3為自由梁的一階振動模態，當外界激勵作用位置目標振型斜率變化不大時，帶入式（15）可得

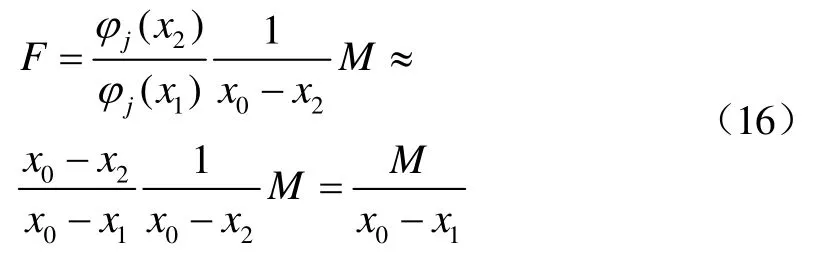
可見，當外界集中力幅值與集中彎矩幅值滿足式（16）的關系時，伯努利梁振動響應為0。

1.3 小結

1）外界激振力作用在伯努利梁某階振型的節點時，無法激起該階振型；作用在某階振型波腹處或自由端處時，振動響應最大。因此，減振器若安裝在目標振型的節點處將無法生效，應盡量安裝在波腹處或自由端。

2）外界激振力矩作用在伯努利梁某階振型的波腹處時，無法激起該階振型；作用在某階振型節點處時，振動響應最大。因此，從減振角度考慮，應盡量將主機布置在接近目標振型波腹，并遠離節點的位置。

3）當伯努利梁上同時作用頻率相等的集中力和集中彎矩，且力和彎矩的幅值滿足式（16）所示的關系時，振動響應可以抵消。此結論可作為減振器激振力幅值的計算依據。

2 有限元算例驗證

采用有限元法對上述結論進行驗證，計算某自由梁的固有頻率，并在梁上不同位置分別施加集中力和彎矩，采用諧響應法計算梁上某點的響應值，繪制頻率響應曲線，對比分析以驗證1.3節中的結論。

圖4 一維梁模型以及前3階振型

算例中的目標振型取第二階振型，對應固有頻率為20.485 Hz，如圖4所示。計算6種工況，按表1所示，分別在梁的不同位置施加力和彎矩，采用諧響應法計算同一點（本算例中取梁的右端點）的頻率響應曲線，進行比對。

圖5～圖7為6種計算工況下梁右端點的頻響曲線，觀察20.485Hz對應的響應值，即圖4中第二階振型對應的響應值，可見圖5～圖7分別驗證了1.3節中的3條結論。

3 實船驗證

本文1.3節的結論在實船主動減振器的安裝過程中有非常實際的指導作用，可作為減振器選型和安裝位置選擇的依據。某小型集裝箱船采用了瓦錫蘭的 6缸主機，該主機在 NCR工況下存在1400kN·m 的二階垂向不平衡力矩，且該船的船體梁二階垂向振動固有頻率大約2.35Hz，如圖8所示，與主機常用轉速72轉/分鐘下的主機二階激振頻率接近，存在共振風險。進一步計算該船在主機二階垂向不平衡力矩作用下的振動響應，發現生活區的振動存在超標風險，考慮增加主機二階主動減振器以抵消主機二階垂向不平衡力矩造成的結構振動。

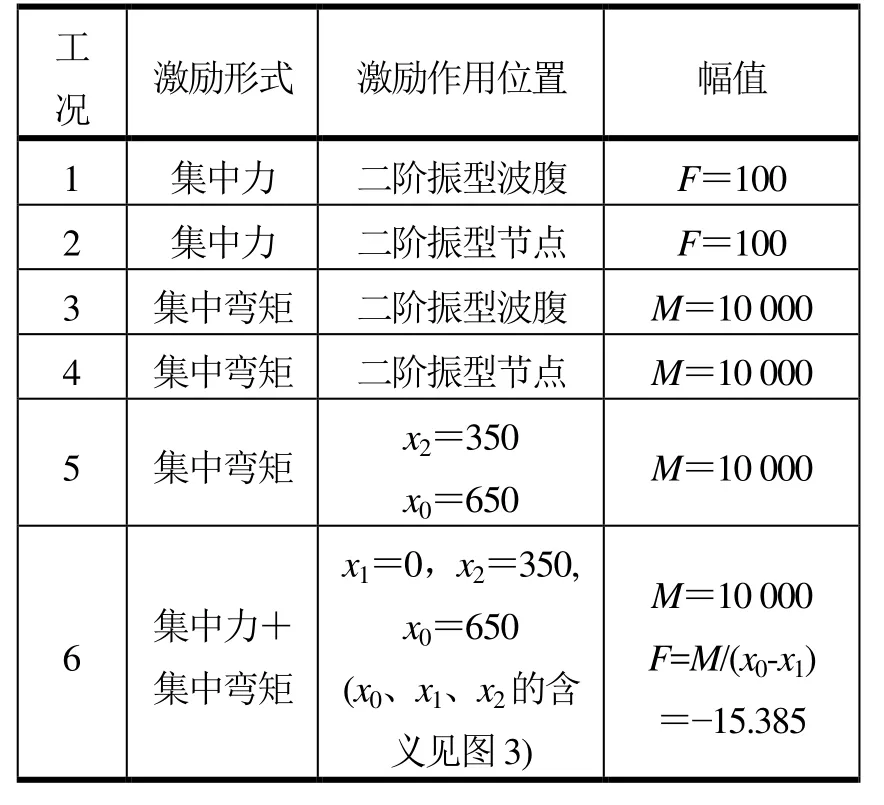
表1 6種計算工況

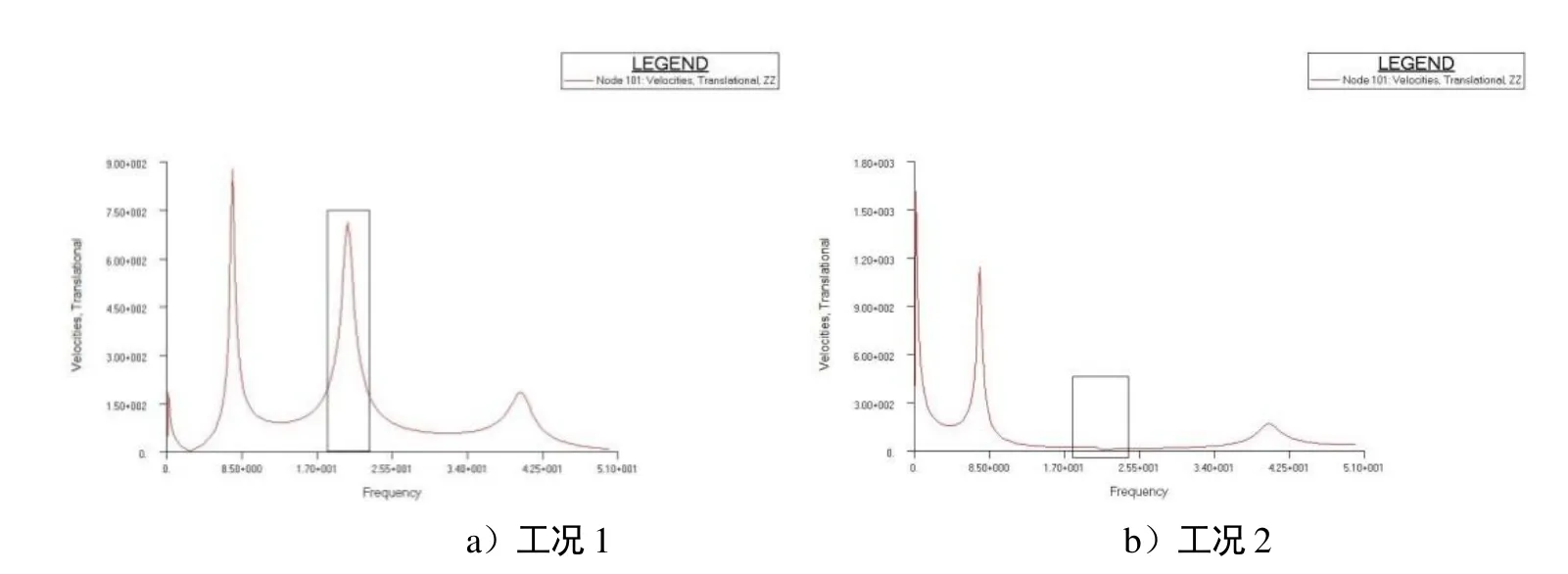
圖5 工況1和工況2下自由梁上某點的振動頻響曲線

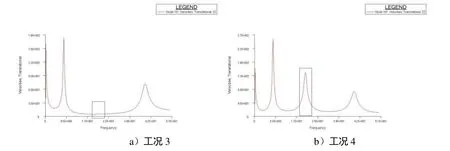
圖6 工況3和工況4下自由梁上某點的振動頻響曲線

圖7 工況5和工況6下自由梁上某點的振動頻響曲線

圖8 某小型集裝箱船船體梁三階垂向振動

根據1.3節中的結論3），減振器安裝位置離振動節點越遠，需要的激振力越小；再充分考慮實船的空間布置和剛度搭配等因素，最終確定將減振器安裝在舵機艙內，如圖9所示，根據式（16）計算得出的激振力幅值53kN。

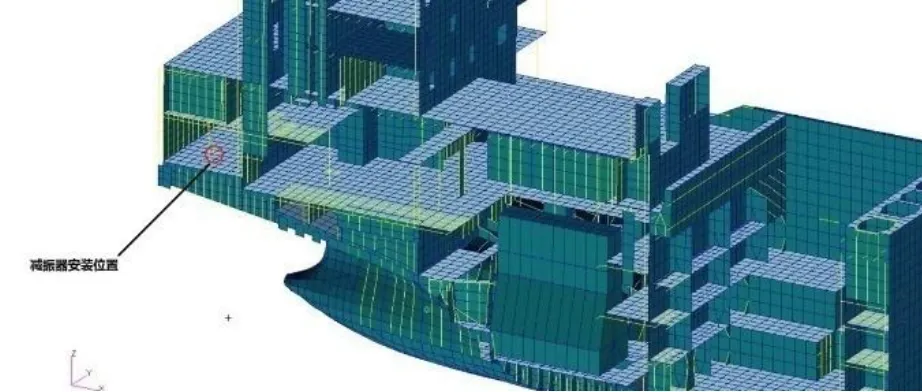
圖9 減振器安裝位置

分別計算安裝二階減振器前后的船舶振動響應，在駕駛甲板上取同一測點，繪制其振動頻響曲線[5,6]，對比2種工況下的振動響應值，如圖10所示。由此可見，安裝減振器前，在 2.35Hz附近,頻響曲線存在明顯的共振峰，且振動速度幅值超過20mm/s；安裝減振器后，2.35Hz附近的共振峰明顯被削弱，振動速度幅值被減弱到了5mm/s以下，效果明顯。

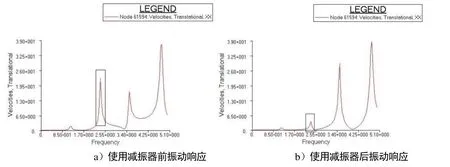
圖10 使用減振器前后駕駛甲板某測點振動響應曲線

4 結論

本文采用自由伯努利梁模擬自由船體梁，通過對其受迫振動機理的研究，得出了梁的振動響應與激勵形式和激勵位置間的關系，提出了3條在船舶減振設計中具有指導作用的結論。采用有限元法分別對其進行了驗證，并在實船項目中證明了該結論的有效性。從作用機理上明確減振器安裝位置對減振效果的影響，為船廠設計減振器的選配和安裝位置提供理論指導依據。