基于ISM 參數偏差階梯式變化的ARAIM可用性

史進恒，劉建業，2，曾慶化，2，孟 騫，2

（1.南京航空航天大學導航研究中心， 南京211106；2.衛星通信與導航協同創新中心， 南京211106）

0 引言

高級接收機自主完好性監測（Advanced Receiver Autonomous Integrity Monitoring，ARAIM）技術是在傳統接收機自主完好性監測（RAIM）［1］技術基礎上發展起來的基于雙頻多星座衛星導航系統的完好性監測技術，它相比傳統RAIM的一個重大區別是新增了地面監測系統，用以產生和更新完好性支持信息（Integrity Support Message，ISM）。當機載導航接收機接收到多星座衛星導航系統播發的雙頻測量值，會結合ARAIM地面監測系統提供的完好性支持信息，計算一系列性能指標并與可用性指標對比，確定當前ARAIM是否可用。

ISM參數可以直接反映空間衛星的服務性能和發生故障的潛在概率，是實現ARAIM的核心要素之一。一方面，ISM參數的精確程度直接影響著ARAIM故障診斷與隔離的準確度和有效性。若ISM參數過于樂觀，ARAIM將無法確保所需的服務安全水平；若ISM參數過于保守，ARAIM的可用性將無法充分發揮。另一方面，目前尚無權威的方法或映射規則等可以獲取ISM各參數的準確數值，ISM中各個參數數值的精確確定是目前限制ARAIM發展的難點之一。現階段，針對ARAIM的仿真和實驗均普遍采用ISM的經驗值展開，該經驗值是基于對衛星和星座各性能的長期觀測數據，應用統計分析的方法得出。

目前，國外對于ISM的研究進展處于領先水平。由美國和歐盟聯合成立的ARAIM技術工作組先后公布了3份里程碑報告［2］，其中編制了ISM的播發電文格式以及在ISM參數經驗值下的ARAIM可用性仿真結果；美國Stanford大學在分析空間信號誤差的基礎上，給出了先驗故障概率的一系列定義，并用實際觀測數據證明了所采用的衛星和星座在先驗故障概率的數量級方面的有效性［3-6］；MITRE公司分析了ISM各個參數偏差對ARAIM完好性和連續性風險的影響情況［7-8］，但其研究主要是分析ISM各參數對造成ARAIM性能變化的兩個中間參數的影響，沒有直觀分析ARAIM最終可用性的變化情況；美國Illinois理工學院對地面監測、ISM的有效性驗證以及連續性風險方面進行了深入研究，但還缺乏實質性的測試和驗證。

近年來，國內針對ARAIM的研究成果也不斷增多，南京航空航天大學針對單星中斷、位置估計優化方法和ARAIM故障模式確定方法進行了研究，并基于北斗/GPS雙星座進行了ARAIM性能的測試和驗證［9-11］；武漢大學對北斗的空間信號誤差及其在ARAIM的應用進行了研究［12］；北京航空航天大學針對衛星標稱誤差對可用性的影響進行了較為全面的研究［13］；上海交通大學搭建無人旋翼機驗證平臺利用北斗信號對ARAIM的基準算法進行了驗證［14］。以上研究尚處于ARAIM的可用性驗證和接收機算法的仿真實現層面，明確針對ISM的研究很少。

現階段ISM參數數值確定尚無廣泛認可的權威方法，基于此現狀，本文針對ARAIM可用性對ISM各參數偏差的靈敏度開展研究。此處的參數偏差指代ISM參數相對經驗值偏離的數值，靈敏度指代因ISM參數偏差導致的ARAIM可用性的變化程度。當ISM某參數產生偏差，即該參數值偏離經驗值時，ARAIM可用性會上升或下降，即某用戶位置是否滿足ARAIM可用性情況可能發生變化，當實際不滿足ARAIM可用性處被誤判為ARAIM可用，會造成嚴重后果。本文對ISM參數的偏差基于經驗值展開，利用階梯式變化在經驗值上下浮動50%，間隔10%產生ISM參數偏差序列，并通過仿真得到ARAIM對應的全球性仿真數據，最后對可用性進行統計和對比。

上述研究的意義和價值主要包括兩個方面，一方面是分析ISM參數發生偏差時對ARAIM可用性的影響；另一方面，在未來ISM參數數值確定中，本文研究所得靈敏度結果對于ISM參數的精確度和更新頻率有直接的參考意義。

1 ISM參數和ARAIM參數分析

1.1 ISM參數分析研究

ISM主要由表1中的5個參數組成。其中，Psat和Pconst可用于確定故障模式［15］；σURA和σURE反映的是衛星實際運行軌道和廣播星歷之間存在的差異，σURA為導航系統精度性能的重要評估指標，σURE間接影響接收機的定位精度；bnom為無衛星故障情況下的最大標稱偏差。

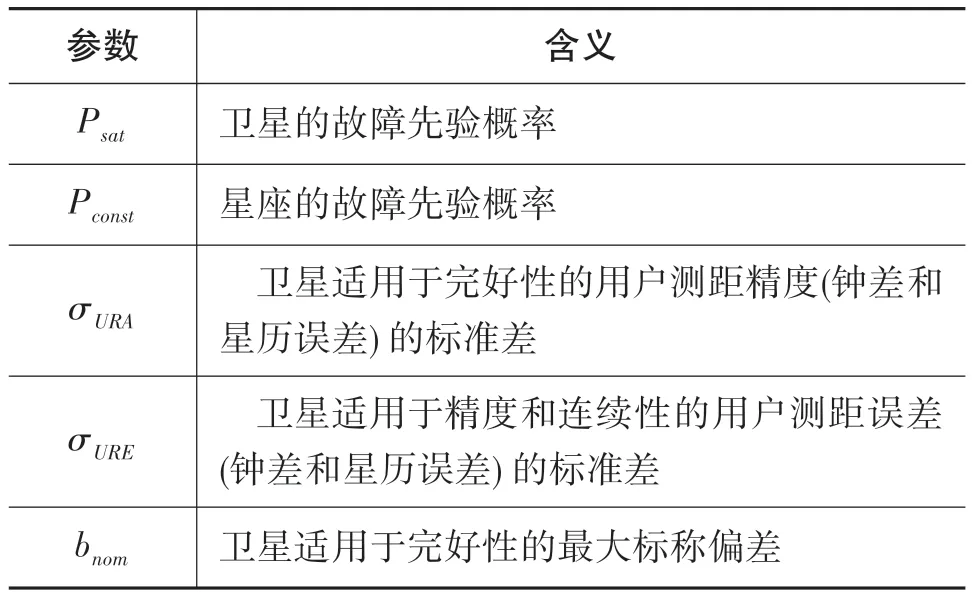
表1 完好性支持信息組成參數Table 1 Component parameters of integrity support message

1.2 ISM參數與ARAIM參數的理論計算關系分析

ISM參數影響ARAIM各個參數的實現過程［16］如圖1所示。圖1中，左側方框中的是完好性支持信息的5個參數，它們是ARAIM的輸入數據；Cint和Cacc分別為用于完好性和用于精度及連續性的偽距對角協方差矩陣，W0為加權矩陣，S0為無故障下的位置估計矩陣，k為故障模式數或故障子集數，Wk和Sk為對應故障模式數下的加權矩陣和位置估計矩陣，σk、bk和σss分別為該故障子集定位解的位置估計方差、最大偏差和無故障位置估計之間定位差異的方差；Nfault為故障模式數量，Pfault為故障先驗概率，Pnot為未檢測風險概率，PHMInew為根據未檢測風險概率更新過的危險誤導信息概率，Pfa為連續性風險概率，Kfa為標準正態分布的閾值，Tk為檢驗統計量的閾值；結合上述參數值可以得到ARAIM性能參數（圖1右側）：垂直定位精度σacc、保護水平PL（垂直保護水平VPL和水平保護水平HPL）和有效監測閾值EMT。

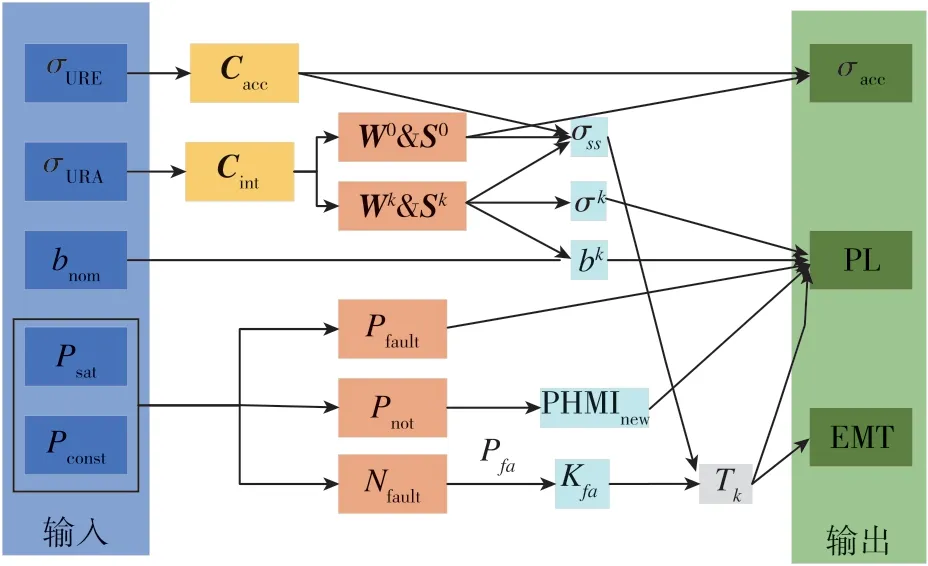
圖1 ISM參數計算ARAIM性能參數過程Fig.1 How ARAIM parameters is calculated from ISM parameters

綜上可以得出5個ISM參數分別對ARAIM參數產生的影響情況：σURE和σURA對ARAIM的各輸出性能參量均會產生影響，bnom只對保護水平有影響，Psat和Pconst對除定位精度以外的性能參量有影響。

1.3 基于軟件接收機的ARAIM算法平臺構建

本文構建了包含ARAIM算法的軟件接收機平臺，其主要功能通過圖2所示的算法實現。算法首先通過計算一系列參數確定子集和相關概率，據此計算容錯解和誤差值。接著遍歷所有需監測故障模式，從中剔除無法觀測的故障模式。然后計算解分離測試閾值并檢測，沒有通過檢測的定位解對應的故障模式發生了，需要進行故障隔離和排除。此后計算相應的ARAIM性能指標，后續將根據這些參數值計算ARAIM算法的可用性并繪制圖像。

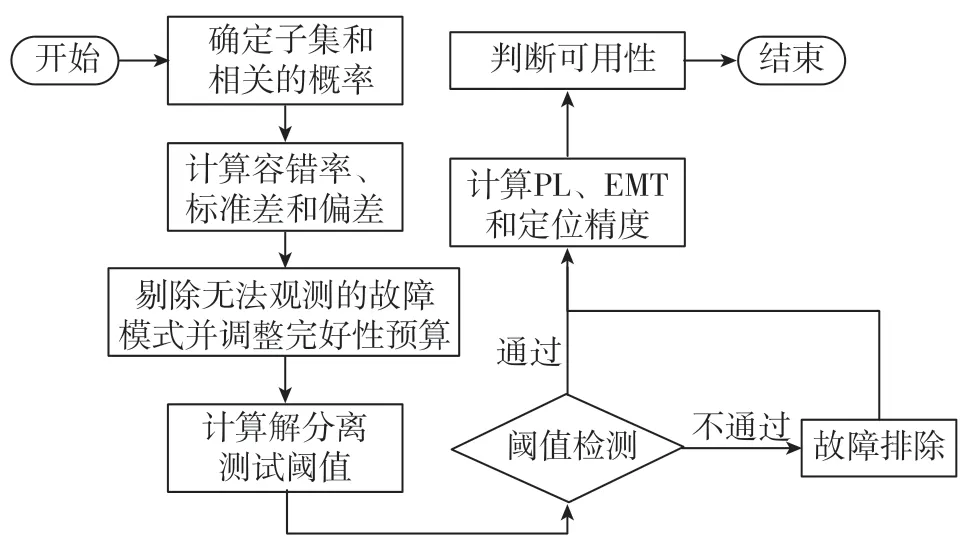
圖2 軟件接收機核心算法Fig.2 Core algorithm of software receiver

2 ISM參數偏差階梯式變化對ARAIM可用性影響的方案設計

2.1 仿真條件

為了在實驗中消除不必要的影響，做以下假設：

1）使用兩個星座，分別為GPS和北斗MEO；

2）真實GPS系統性能與廣播ISM中反映的性能完美匹配；

3）真實北斗系統性能與廣播ISM中反映的性能單獨出現偏差；

4）不考慮不同星座、不同衛星之間的差異等信息不準確性可能會引起仿真結果的誤差；

5）上述兩星座ISM參數值設定如表2所示。

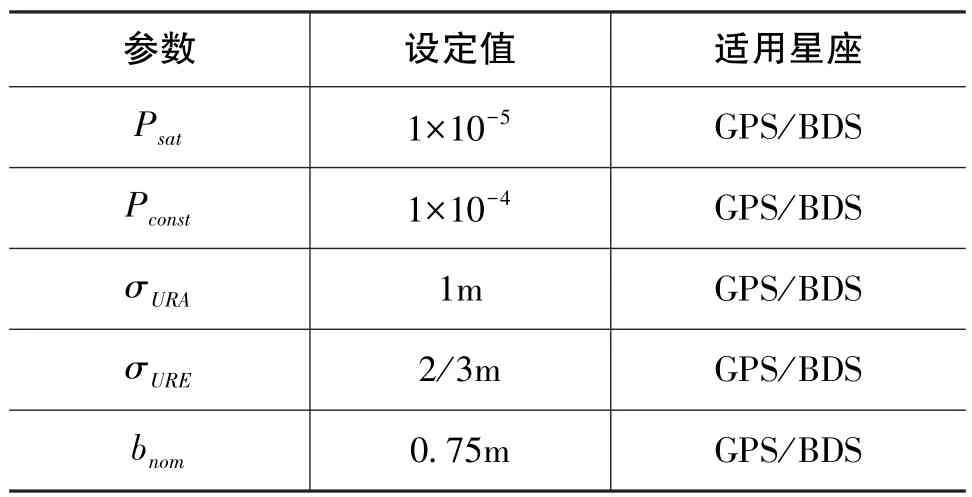
表2 反映星座真實性能的ISM參數值設定Table 2 ISM parameter values matching the true performance of the constellation

2.2 階梯式變化研究方案設計

研究采用的ISM參數值均為里程碑報告三中給出的經驗值，經驗值的±50%范圍幾乎涵蓋了各參數所有可能出現的值。為了研究ISM參數偏差對ARAIM可用性的影響，本文設計了基于單參數變化的階梯式研究方案：每次只改變一個參數值，在該參數經驗值-50%～50%范圍內，以經驗值的10%為間隔依次遞增。

最新的北斗三號系統對基本空間星座的構型優化為“3顆GEO衛星、3顆IGSO衛星和24顆MEO衛星，并視情部署在軌備份衛星”，鑒于GEO和IGSO的服務不具備全球性，本文中的北斗基準星座只考慮24顆MEO衛星。

具體仿真實驗中，采用基于軟件接收機的ARAIM算法平臺，調用24顆北斗MEO衛星和24顆GPS衛星的星歷歷書，進行一系列參數設定并運行仿真程序，將ARAIM的4個主要性能參數HPL、VPL、EMT和σacc及許多內部中間參數作為模擬時間和模擬位置的結果數據集輸出并進行具體分析。

現將階梯式變化研究方案中設定的ISM參數值列于表3中。

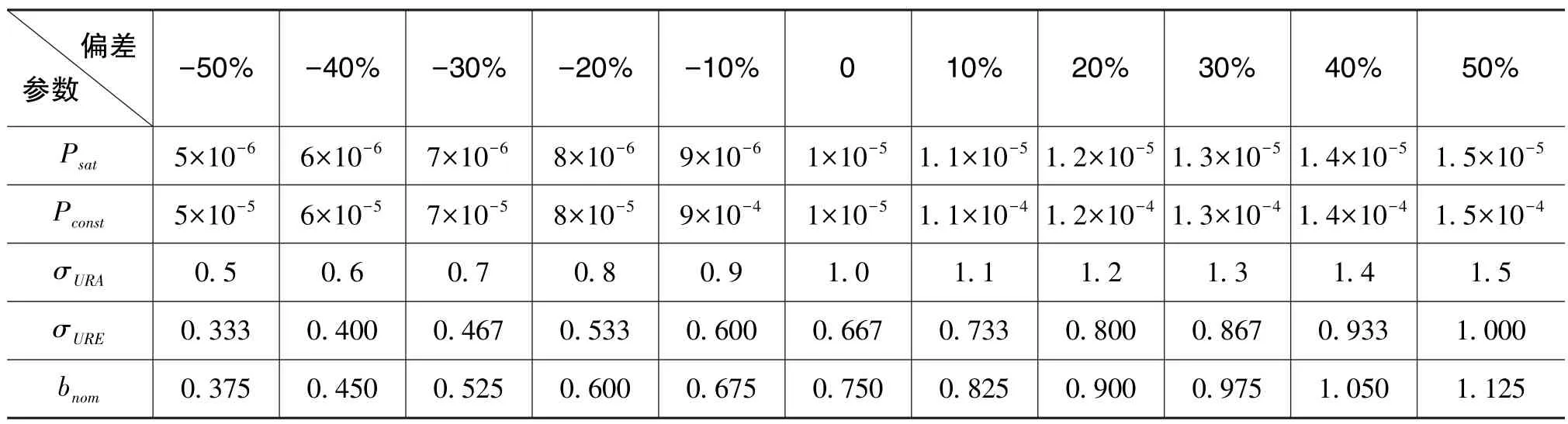
表3 設計方案中ISM參數值設定Table 3 Setting of ISM parameter values in the design scheme

2.3 基于ARAIM算法平臺的仿真實驗

在搭建的ARAIM 算法仿真平臺中，當某一參數值變化時，其他參數均設定為無偏值，逐次改變變化參數的設定值為表3中的設計值進行仿真實驗。此前，需進行一系列設置：

1）仿真時長為7天，對應于北斗星下點軌跡周期；

2）仿真步長為10min；

3）地球表面網格劃分為10°×10°的地球表面經緯網格。

由上述設置可知，在每次仿真過程中，每個ARAIM性能參數都會生成一個648×1008的數據表格，用于存儲每一個用戶位置處的性能參數值。

為了更直觀地展現在特定ISM輸入時ARAIM的可用性及各性能參數值在全球范圍的分布情況，將仿真實驗結果展示在世界地圖中。以ISM各參數均沒有產生偏差為例，仿真結果如圖3（a）～圖3（e）所示。

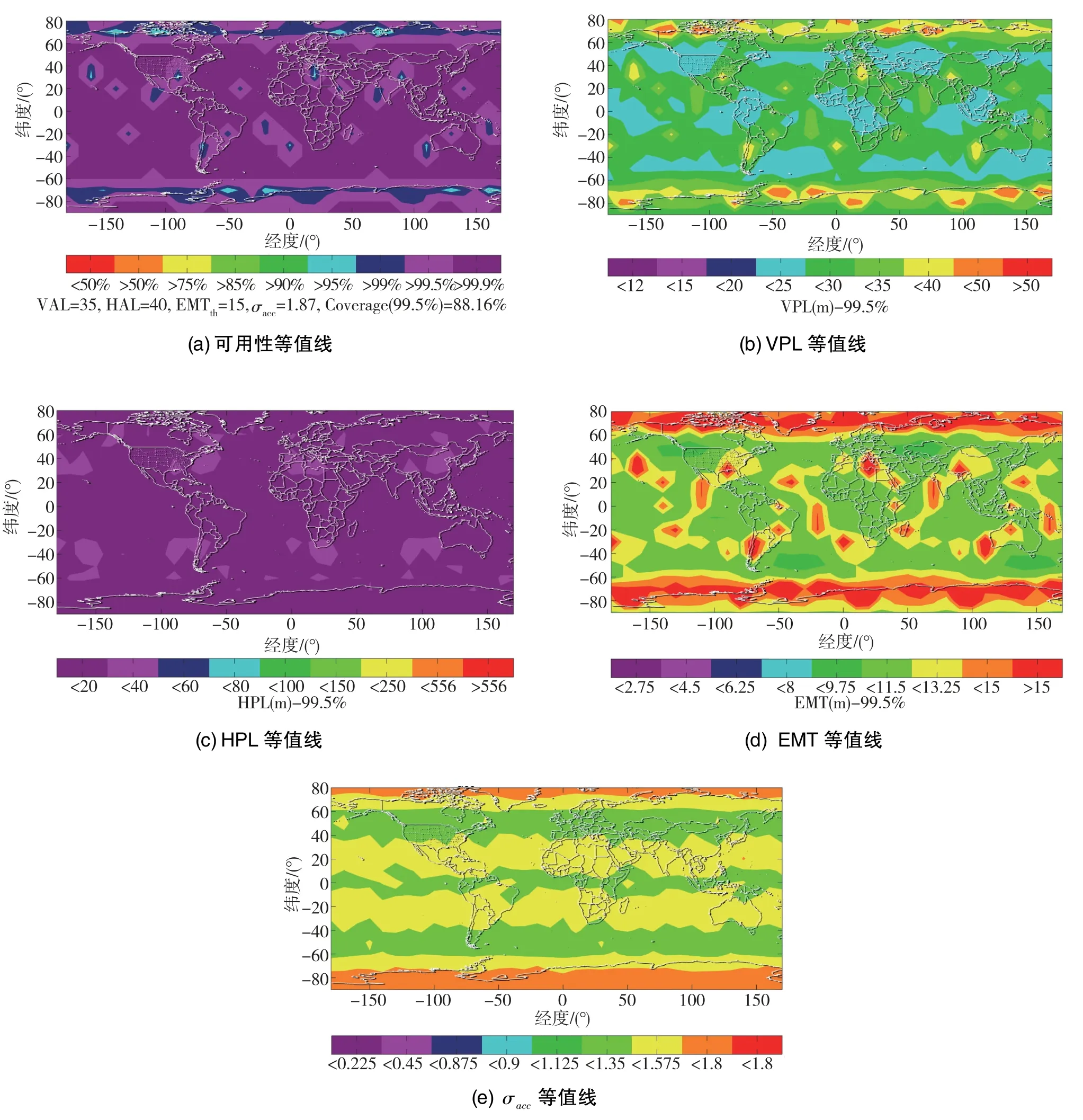
圖3 仿真結果Fig.3 Results of simulation

由圖3大致可以看出，當ISM各參數均沒有產生偏差時，全球大部分地區都可滿足ARAIM性能指標。但結果圖只能呈現一個大致的分布情況，ISM參數偏差對ARAIM性能的具體影響情況還需要通過定量分析得出。

3 仿真結果分析

仿真實驗中共運行仿真程序51次，輸出51組數據，下面將基于實驗數據進行ISM參數偏差對ARAIM可用性影響情況的統計和分析。

3.1 LPV-200可用性判據

垂直引導性能服務LPV-200（Localizer Performance with Vertical Guidance-200）指GNSS可以在飛行航路、終端飛行和低至200ft精密進近等各種階段均可以提供99.0%或者更好的完好性，現階段ARAIM提供引導服務的最終目標是在全球范圍內具備LPV-200的服務性能。本文對北斗/GPS雙系統下ARAIM在全球范圍內針對LPV-200且滿足99.5%完好性的情況進行研究，LPV-200的可用性判據在表4中列出。在特定歷元的特定用戶位置，ARAIM的4個性能指標均滿足要求，ARAIM可用性才滿足可用性。

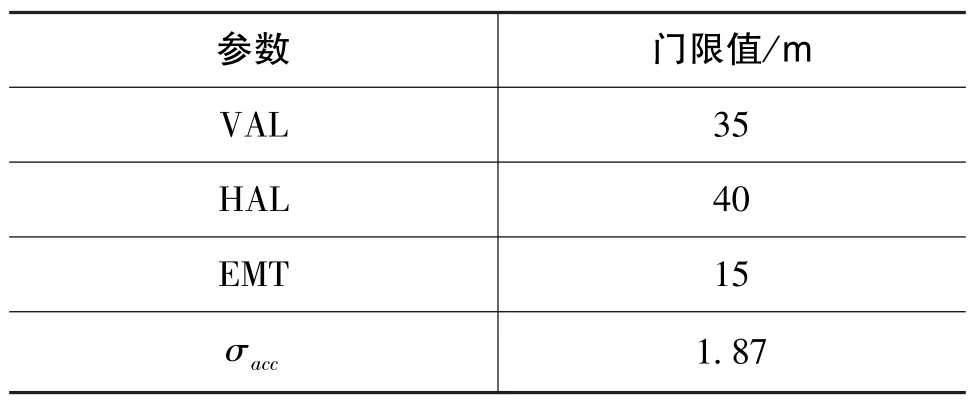
表4 LPV-200可用性判據Table 4 Availability criteria of LPV-200

3.2 仿真實驗結果匯總

在記錄仿真實驗結果時，可用性采用百分數形式表示，其數值為滿足導航性能的時間所占百分比。針對ARAIM的4個性能參數均計算不滿足ARAIM可用性判據的用戶位置數占比，即對應性能參數在各偏差下的統計值越低，滿足性能要求的程度就越高。文中采用如圖4（a）～圖4（e）所示的折線圖直觀展現結果，因為在各仿真點處HPL均滿足性能要求，故圖4中沒有展示HPL相關的數值變化情況。

針對同一ISM參數偏差時ARAIM各個性能參數的數值變化情況進行分析，可獲得以下結論：

1）Pconst和Psat主要通過影響VPL來影響可用性。其中，Psat在產生正向偏差較大時，也會使EMT參數產生變化從而影響可用性。

2）σURE和σURA產生偏差時，ARAIM的性能參數除HPL外均產生了變化：隨著σURE逐漸增大，VPL、σacc和EMT的性能逐漸變差，均一定程度上造成ARAIM可用性下降；而隨著σURA逐漸增大，EMT性能不斷變好，超過VAL門限值以及精度不滿足要求的點數呈先減后增趨勢，即VPL和σacc的性能先變好后轉差，但其性能轉差沒有EMT性能變好給ARAIM產生的影響大，所以總體ARAIM的可用性不斷增加。

3）無論ISM哪個參數值偏差，輸出值在HPL性能上均滿足要求。一方面，因為水平方向的導航引導相對垂直方向更容易實現；另一方面，ARAIM相比傳統RAIM采用了雙頻多星座，具有更好的性能，所以滿足水平方向的要求更加容易。

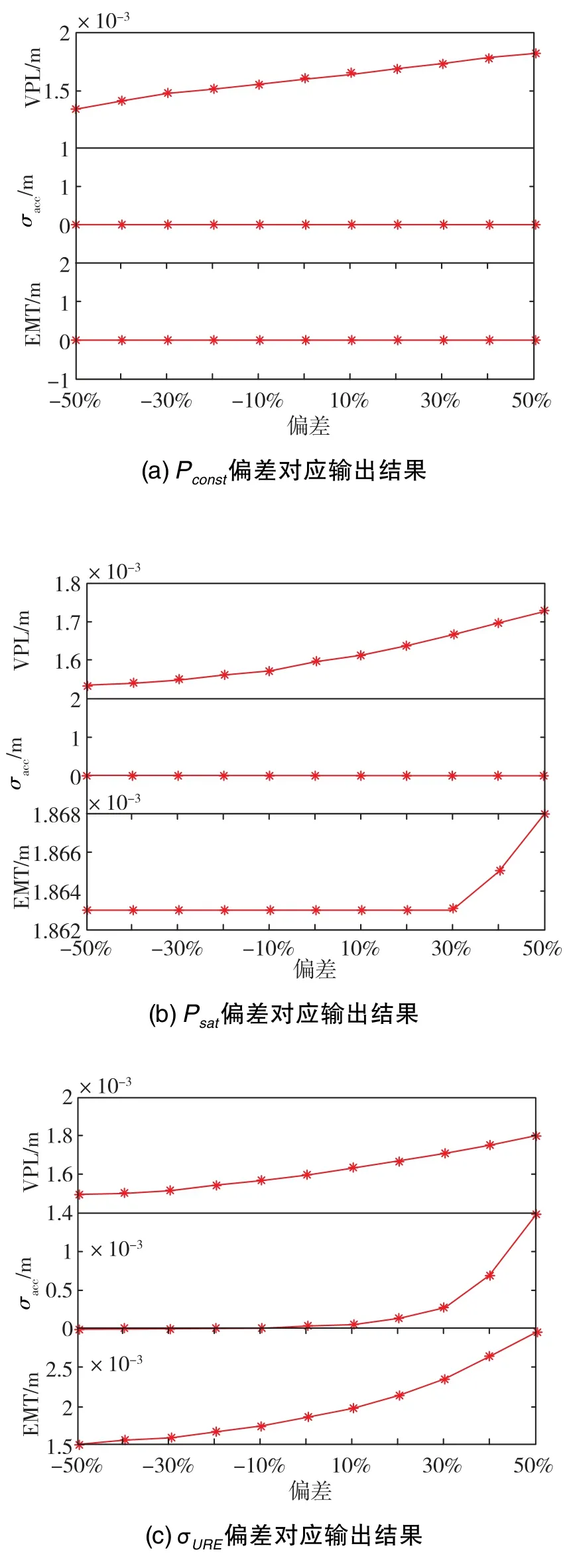
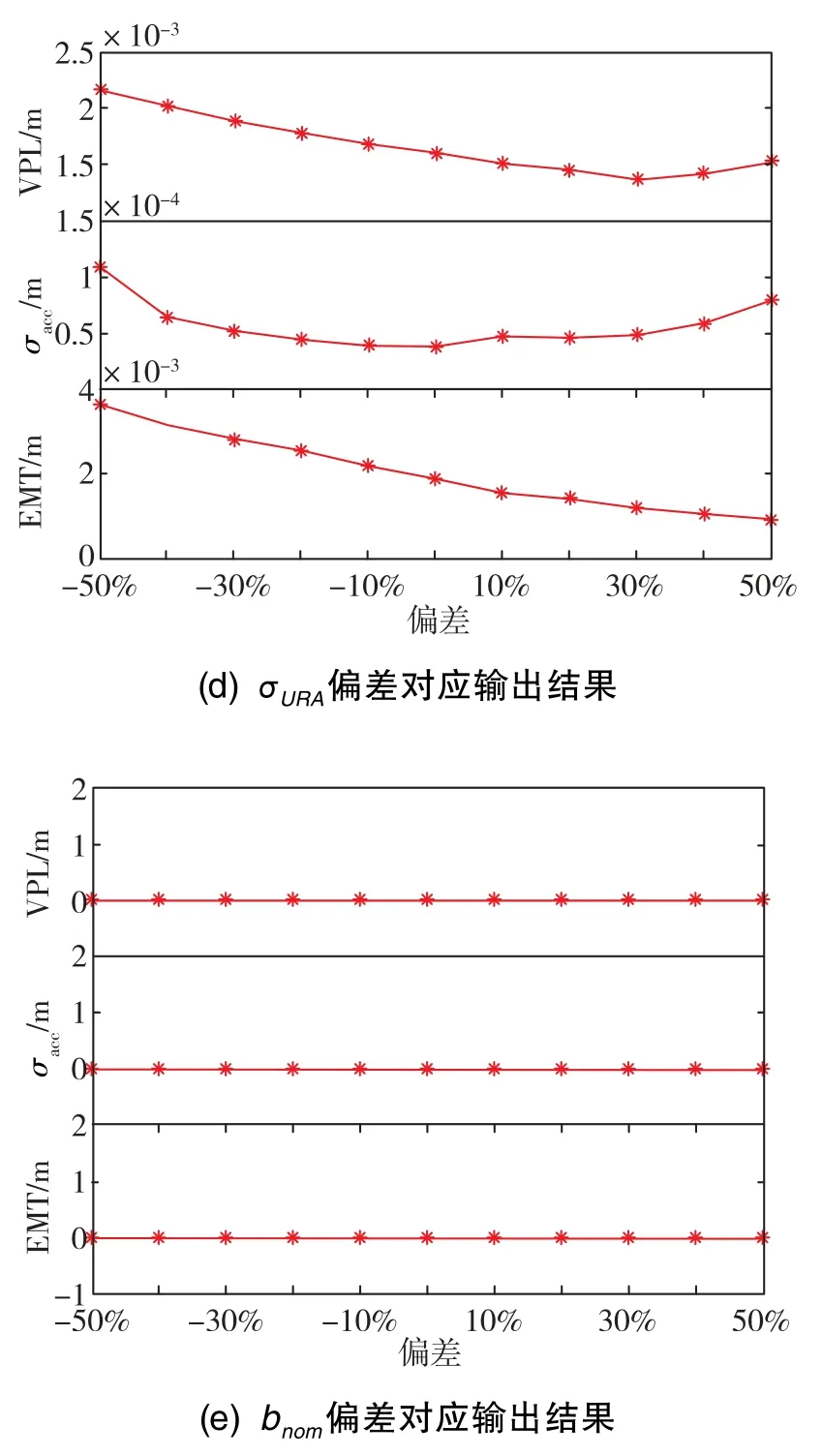
圖4 ISM參數偏差對應的輸出結果Fig.4 Output results corresponding to ISM parameter deviation

3.3 ISM參數偏差對ARAIM可用性的影響分析

將ISM各參數變化時的ARAIM可用性大小繪制成折線圖，圖像采用主副坐標軸。其中，Pconst、Psat和bnom采用左側坐標軸，σURE和σURA采用右側坐標軸，如圖5所示。由圖5可知，ARAIM可用性隨著ISM參數值變化而變化：當Pconst、Psat和σURE變大時，可用性呈下降趨勢；當σURA變大時，可用性呈上升趨勢；當bnom變大時，可用性不變。即當完好性偏差在一定范圍變化時，對可用性影響極小。

但不管ISM參數如何變化，絕大部分情況下的ARAIM可用性都未超過90%，超過90%的情況占比不到1/5。所以采用的ARAIM基準算法有一定的改進空間，通過適當優化可達到更高的可用性，相關內容在后續研究中將進一步深入。

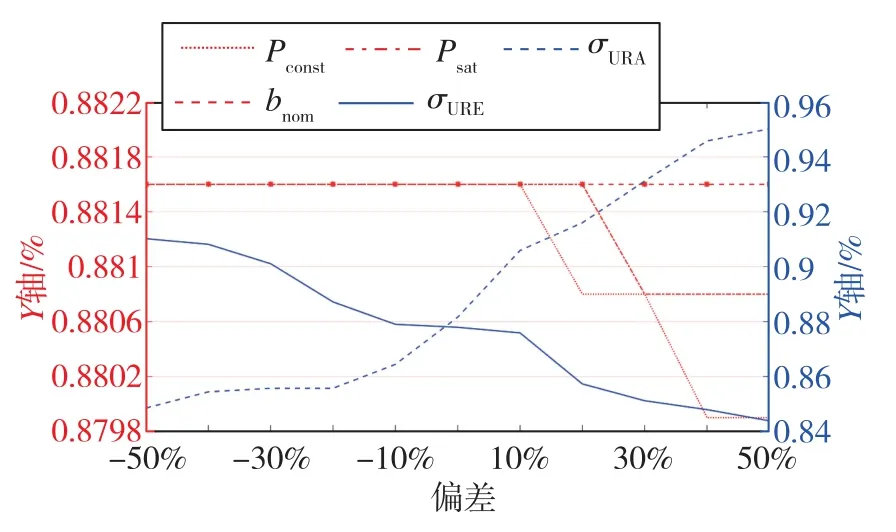
圖5 ISM各參數變化對ARAIM可用性的影響Fig.5 Impact of ISM changes on ARAIM availability

3.4 ISM某一參數偏差對ARAIM某一性能參數的影響分析

不同ISM參數變化時，對ARAIM單個或多個性能參數產生影響，進而不同程度上造成ARAIM可用性變化。由于ISM某一參數產生偏差對ARAIM某一參數影響事件的組合較多，本文選取Pconst變化對VPL的影響情況進行分析。

本文選取緯度40°、Pconst產生不同偏差時的VPL參數值變化情況進行分析。由于輸出值較多，為了使結果更清晰地展現，分別選取-50%、-30%、-10%、0、10%、30%和50%偏差處的情況繪制圖像，如圖6所示。由圖6可知，同一緯度上位于同一經度圈的兩點在數值上具有相似性。

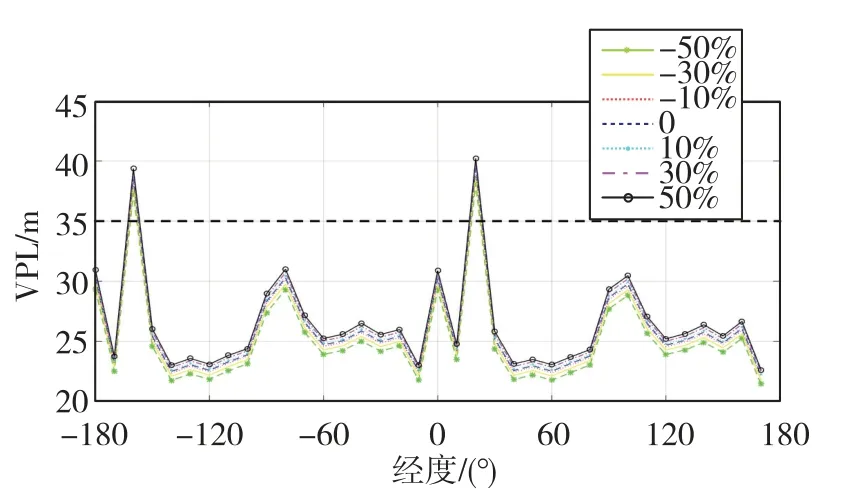
圖6 緯度40°時Pconst變化對VPL的影響Fig.6 Impact of Pconst changes on VPL at 40° latitude

此外，本文還以Pconst無偏差時的情況為例，分析在滿足99.5%可用性時全球VPL參數值分布情況，如圖7所示。由圖7可知，在99.5%可用性處很多用戶位置不滿足LPV-200性能要求。

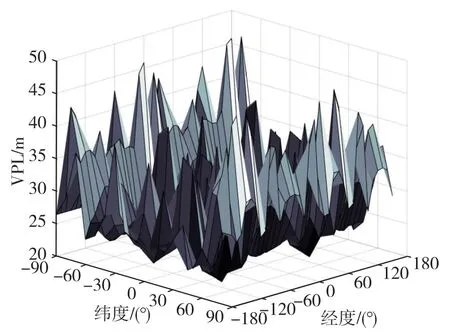
圖7 Pconst無偏差時全球VPL分布情況Fig.7 Global VPL values distribution when Pconst is unbiased

4 結論

本文采用基于軟件接收機的ARAIM算法平臺，針對ISM參數偏差對ARAIM可用性的影響設計單參數變化的階梯式研究方案，進行實驗并對實驗結果分析，得到如下結論：

1）針對ISM各參數如何影響ARAIM參數，仿真實驗與理論分析的結果是一致的。

2）在一定范圍內，ARAIM可用性與Pconst、Psat和σURE成負相關性，與σURA成正相關性。

3）在設定的偏差范圍內，σURA偏差對可用性的影響最大，可用性變化超過10%；σURE的影響其次，產生超過5%的變化；Pconst和Psat的偏差對ARAIM影響很小，而bnom變化對可用性影響極小。

采用階梯式變化對ISM參數在經驗值的基礎上增加不同偏差，可以對ARAIM在ISM參數相比實際數據產生偏差時的可用性進行清晰的量化，從而進一步研究ARAIM對不同ISM參數偏差的靈敏度。同時，本文采用的階梯式變化采用-50%～50%的偏差范圍和10%的偏差間隔，可以較好地涵蓋不同參數可能出現的變化范圍，更直觀地測試變化趨勢。

在現階段ISM參數的確定方法尚無權威定論的情況下，采用階梯式變化圍繞經驗值進行ARAIM靈敏度的研究，對ISM參數的精確度和更新頻率的研究更具有現實意義和參考價值。本文主要分析ISM單參數變化對ARAIM性能的影響情況，后繼將結合算法理論深入研究，并分析ISM多參數變化對ARAIM性能的綜合影響情況。