盾構隧道同步注漿縱環向整體擴散理論模型

李培楠，石 來，李曉軍，劉 俊

（1. 同濟大學土木工程學院，上海200092；2. 東華大學環境科學與工程學院，上海201620；3. 上海工程技術大學城市軌道交通學院，上海201620）

盾構工法是城市地下空間開發的主要施工方法之一，刀盤掘進、管片拼裝和同步注漿構成了盾構工法的三大要素。同步注漿在控制環境擾動、隧道抗浮防滲等方面起到關鍵作用，然而由于不可見性，具有較大的不確定性和風險性。注漿參數的設定直接影響注漿效果，而針對漿液材料特性及地層環境特點如何正確取值則依賴于注漿機理分析及其擴散模型的指導。

長期以來，不少學者對漿液擴散機理和理論模型開展了相關研究。張慶松等［1］研究速凝類漿液在水平裂隙中的擴散流動過程，并考慮了漿液黏度的時變性，建立了水平裂隙注漿擴散理論模型。張連震等［2］在此基礎上，考慮了漿液和巖體之間的相互作用，并建立了可完整描述考慮耦合作用的注漿擴散過程的數值算法。裴啟濤等［3］則進一步將該注漿擴散理論推廣到傾斜裂隙注漿。

盾尾注漿是盾構同步注漿的主要形式。針對盾尾同步注漿擴散模型，許多學者也進行了研究。Bezuijen 等［4-5］分析了漿液從填充、滲透到壓密的整個擴散和固結過程，并結合現場注漿測試研究，探究不同階段漿液壓力的變化。葉飛等［6-8］將漿液在盾尾間隙內的擴散過程理想化地歸納為充填、滲透、壓密及劈裂等4個階段，并分別展開了理論分析研究。李志明等［9］分別采用牛頓流體及Bingham 流體推導出了在黏土地層中同步注漿填充擴散的力學模型。袁小會等［10］基于Bingham 流體本構，推導出了注漿壓力時空衰減規律以及擴散距離與注漿時間的關系。梁禹等［11］在已有的研究基礎上，綜合考慮了同步注漿過程中的漿液填充、擴散與后續因滲流引起的壓力消散過程，并得到了漿液壓力沿管片環縱向分布的理論計算公式。

分析上述學者的研究內容，可以發現漿液在盾尾間隙內的環向填充和縱向擴散往往被看作兩個相互獨立的運動模式，關于漿液縱環向整體擴散理論模型的研究較少。本文在現有的漿液擴散理論研究基礎上，分析盾尾同步注漿縱環向整體擴散機理，建立盾尾同步注漿空間擴散理論模型，并提出求解該模型的數值算法。此外，依托大直徑圓形盾構隧道工程實例，對模型進行驗證和分析。

1 盾尾同步注漿擴散機理

1.1 機理分析

文獻［8-9］和文獻［11］中的理論推導主要研究漿液環向獨立擴散時的壓力分布情況，其假設在盾尾同步注漿過程中，漿液環向填充可忽略其沿隧道軸向的流動，填充空間被假定成一個均勻的三維環狀薄餅，而漿液縱向擴散也視為環向填充完成后，橫截面內漿液的一致縱向擴散。然而，實際上由于注漿口的出漿速度遠大于盾構推進速度，因此漿液環向填充過程不可忽略漿液的縱向擴散運動，即漿液的擴散模式應是具有縱環向相互關聯的（圖1），上述假設在一定程度上與實際情況有著較大的偏差。

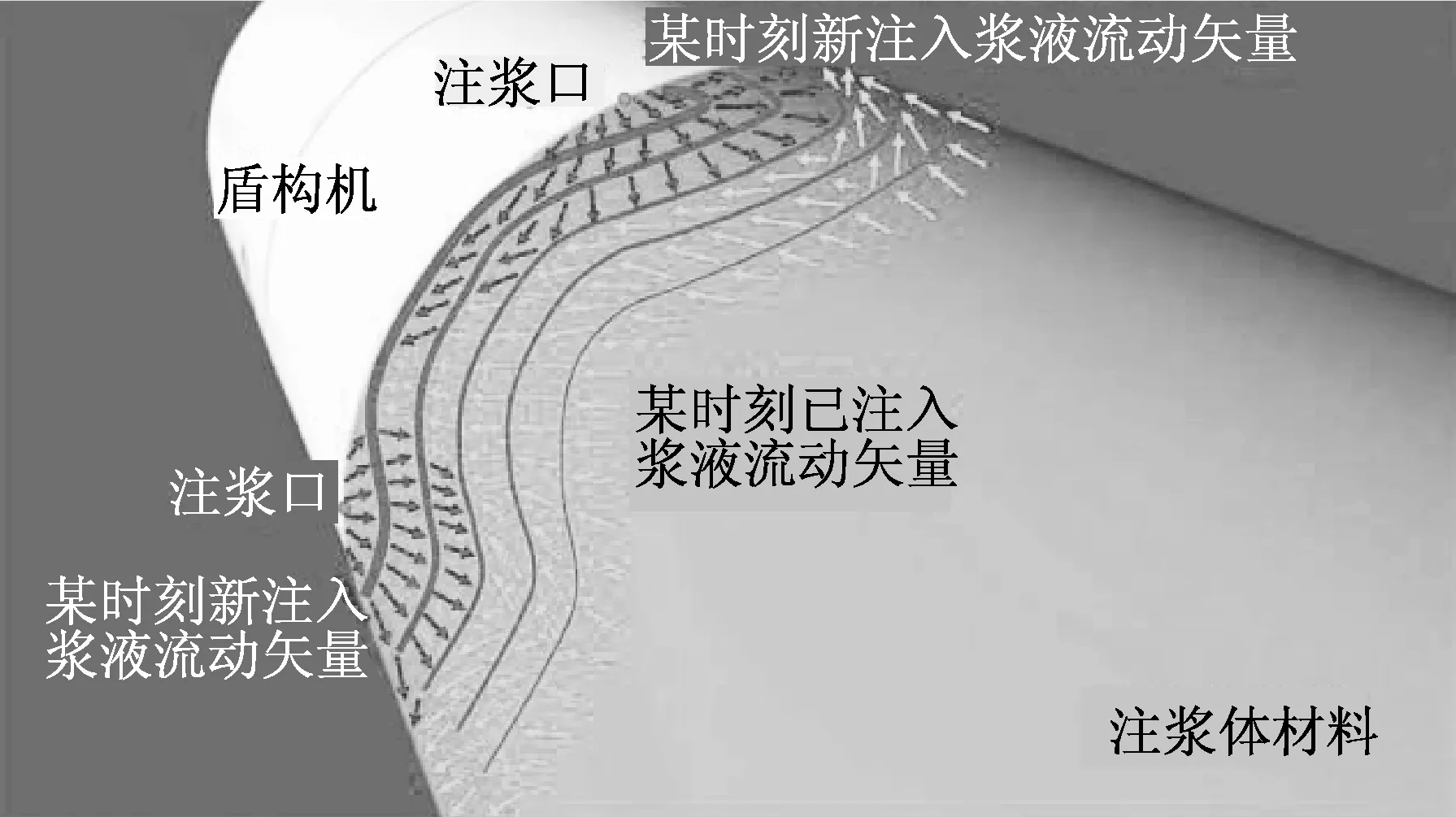
圖1 同步注漿縱環向三維擴散機理示意圖［12］Fig.1 Schematic of synchronous grouting longitudinal-circumferential 3D diffusion mechanism[12]

參考文獻［12］，盾尾同步注漿光滑粒子流體動力學（smoothed particle hydrodynamics，SPH）數值模擬結果顯示漿液注入盾尾間隙是一個空間動態的填充過程，漿液由注漿孔噴出后呈現扇形擴散的模式（圖2），漿液的擴散形態由注漿參數和周圍環境壓力決定。因此，盾構隧道盾尾同步注漿的填充擴散過程整體上應當被看作是具有縱環向相互關聯的擠壓填充性流體運動。

圖2 漿液擴散形態的數值模擬結果［12］Fig.2 Numerical simulation results of grout diffusion form[12]

1.2 基本假設

基于盾尾同步注漿擴散機理分析，為后續理論公式推導提出以下基本假設：

（1）漿液為各向同性不可壓縮的Bingham流體，不考慮漿液損失及黏度等性質變化；

（2）漿液與地層、管片外壁接觸面不發生相對滑移，漿液為層流狀態；

（3）漿液擴散鋒面處壓力等于周圍環境壓力，任意漿液單一質點的流動方向與管片軸線的夾角保持不變；

（4）漿液出注漿孔時的初始擴散鋒面為半圓形，擴散運動平衡方程不考慮加速度影響。

1.3 漿液擴散運動方程

圖3 為盾尾同步注漿漿液擴散示意圖，直線填充部分代表新注入漿液，網格填充部分代表已注入漿液。M 位于漿液擴散鋒面上，N 為M 與注漿孔1連線H1M上的任意一點，Nt為N在隧道橫截面上的投影。圖3中，α1為注漿孔1與所在截面管片中心連線的豎向夾角，αN為N 與所在截面管片中心連線的豎向夾角。假定漿液擴散方向與管片軸線的夾角保持不變，則在管片外表面展開圖中，漿液擴散方向始終與注漿孔與擴散鋒面的連線同向。即如圖4 所示，H1M 連線上任一點N 的速度vN存在vN//H1M，與管片軸線的夾角為θM（逆時針為正）。

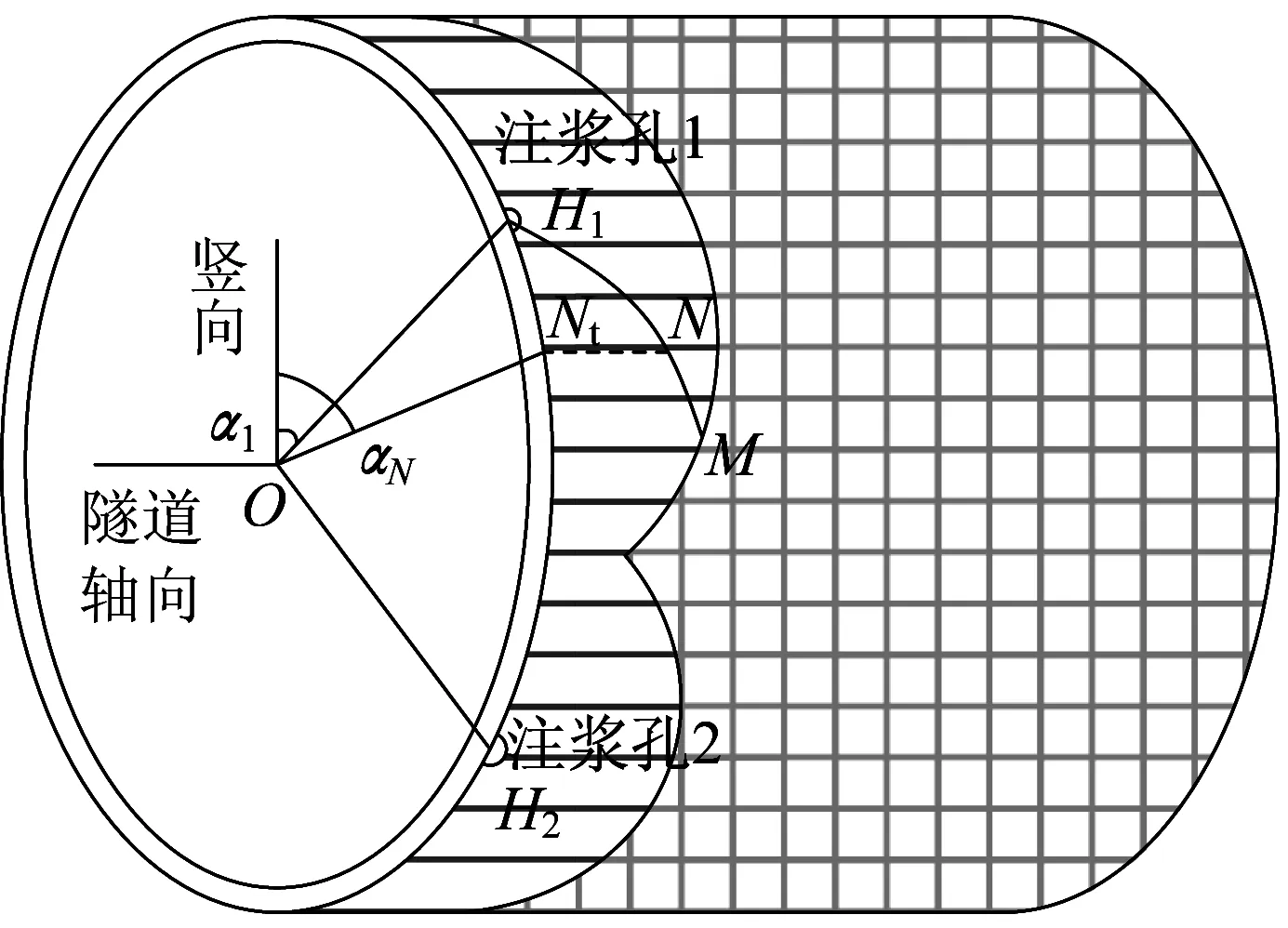
圖3 漿液擴散立體示意圖Fig.3 Stereoscopic diagram of grout diffusion

圖4 漿液擴散平面展開圖Fig.4 Plane stretched diagram of grout diffusion

如圖5所示，取N處漿液微元進行分析。圖中，Z，R，S 分別表示盾尾間隙厚度方向，漿液流動方向和該平面外法向；w 為盾尾間隙厚度；zp為Bingham流體流核半徑；P 為漿液壓力；τ 為漿液運動的剪應力。沿著漿液流動方向對漿液微元進行受力分析，可得：

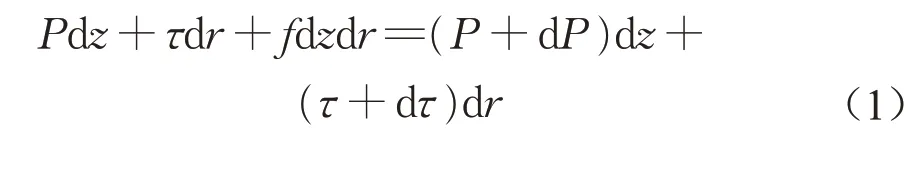
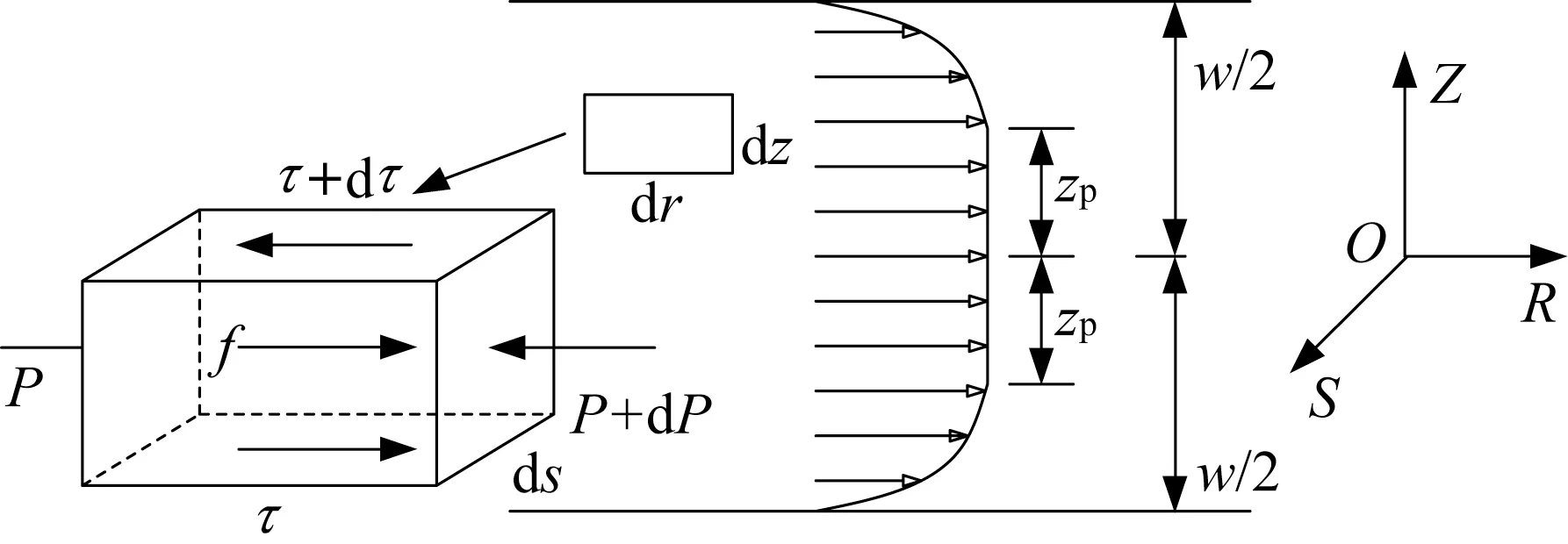
圖5 漿液微元受力分析圖Fig.5 Mechanical analysis of grout element

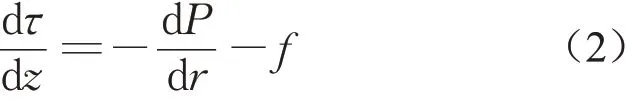
式中：f為重力在R方向上分量，f =ρg sin αNsin θM；ρ為漿液密度；g為重力加速度。

假定漿液為Bingham流體，其本構方程為

式中：τ0為靜切力；μ為塑性黏度系數；γ為剪切速率；v為漿液流動速度。

將式（4）代入式（3）得到：

令τ0=Az/R，可得Bingham流體的流核半徑：

在|z|≤zp范圍內，流體切應力較小，流層之間不發生相對流動；在zp≤|z|≤w/2 范圍內，流體切應力逐漸增大，相鄰層流體處于運動狀態，如圖5所示。

對式（5）進行積分，聯合邊界條件：z=w/2 時，v=0，得漿液在zp≤|z|≤w/2范圍內速度分布：

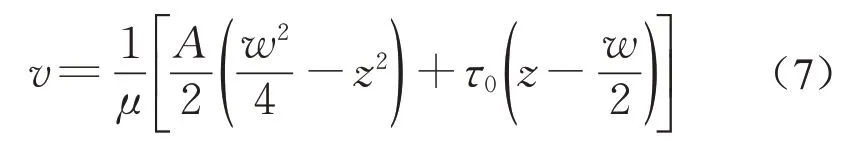
流核半徑內漿液流速一致，則漿液流速沿z方向的分布為

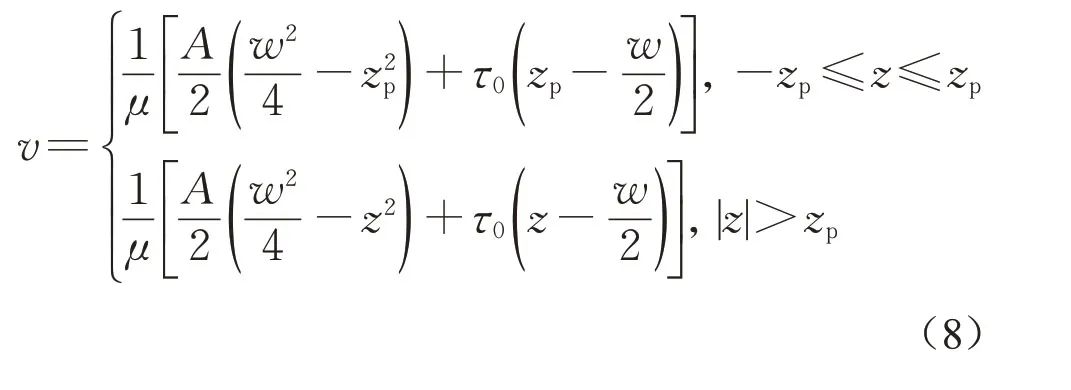
建立微元截面流量與漿液流速的關系式：

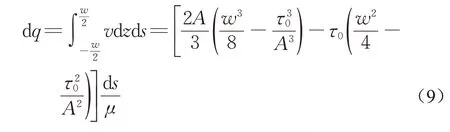
因此，可以得到A的一元三次方程：

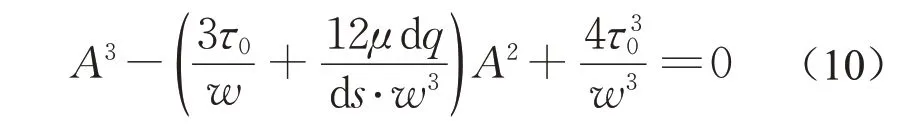
利用式（10），并聯立式（6）的約束條件：zp＜w/2，可解出A的值。

由式（2）可得：

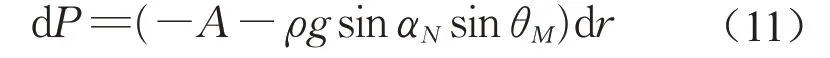
基于漿液質點擴散速度方向始終與管片軸線夾角不變假設，注漿孔與擴散鋒面一點的連線上的各個點的漿液擴散速率的關系式如下：

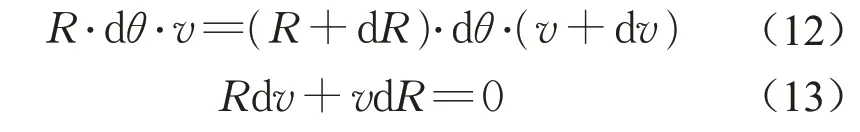
基于漿液擴散鋒面處壓力等于周圍環境壓力的假設，可得漿液擴散運動的控制方程為

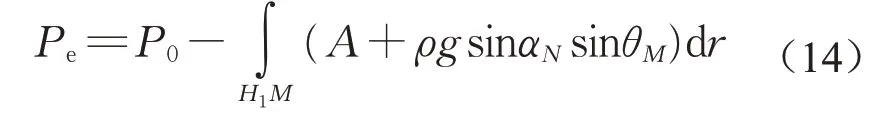
式中：P0為注漿孔壓力；Pe為環境壓力。

2 盾尾同步注漿步進式算法

理論推導得到的計算公式中涉及多個多元非線性方程，且漿液擴散軌跡不規則進而無法直接積分，因此需借助數值方法進行求解注漿壓力。

2.1 求解區域離散化

圖6為注漿孔1漿液擴散范圍的展開圖，將擴散區域離散成n-1 個扇形單元，各扇形單元的圓心角Δθ 相等。此外將每個扇形單元沿著徑向離散成m個等間距的環形單元，環形單元按照等數等分，相應邊長Ri上的離散長度Δri具有自適應性。圖6 中r0為注漿孔等效半徑，rij代表Ri上第j個離散點距離注漿孔圓心的長度。

基于連續性假設，同一扇形單元內的不同環形單元流量相等，則各環形單元漿液擴散速度可由式（13）得到。

基于式（11），可得漿液經過環形單元ri，jri，j+1時產生的壓力損失：

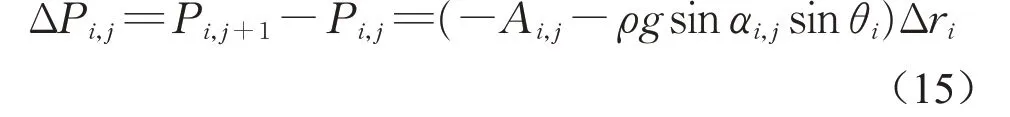
其中，Ai，j=f(ri，j，θi，Δq)，由式（10）計算可得。

式（15）中，環形單元的豎向夾角計算公式如下：

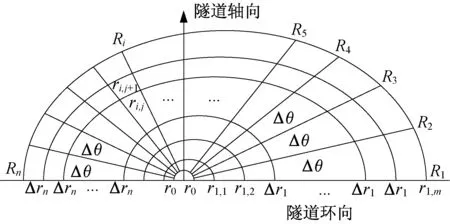
圖6 漿液擴散區域內的離散單元劃分Fig. 6 Division of discrete elements in the slurry diffusion region

式中：Rt為盾構隧道外徑。

2.2 基于弦截法的注漿流量求解

漿液擴散鋒面的速度由注漿壓力和周圍環境壓力的壓力差決定，計算各個扇形單元的注漿流量Δqi需要求解以下的非線性方程組：

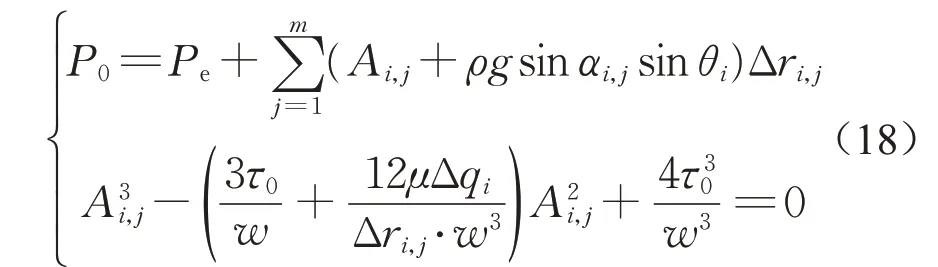
對于該類問題，弦截法是一種有效的數值計算方法。如圖7所示（xs代表方程f(x)=0的精確解），弦截法是一種通過不斷的線性迭代求解非線性方程的數值方法，相較于二分法，能夠快速收斂至零點。弦截法的基本迭代公式如下：

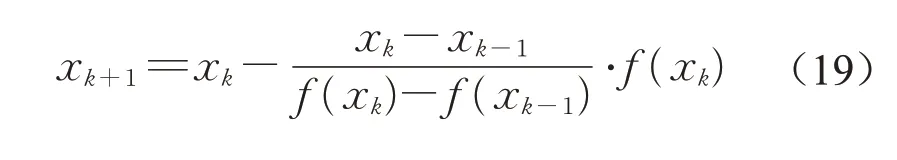
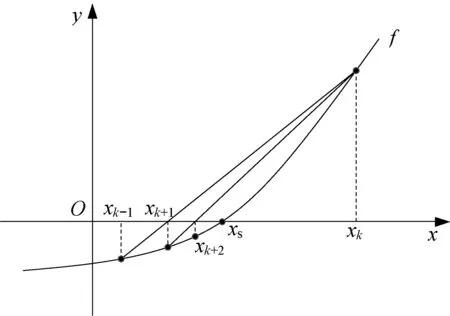
圖7 弦截法迭代計算示意圖Fig. 7 Schematic diagram of secant method iterative calculation

基于式（18），通過編寫相應的算法程序，可獲取滿足誤差要求的各個扇形單元的注漿流量的Δqi數值解。

2.3 漿液擴散鋒面追蹤

注漿擴散壓力的計算前提之一在于明確漿液的擴散鋒面，而擴散鋒面是由不同點處漿液擴散速度決定的。因此，漿液擴散鋒面與漿液擴散速度的求解是一個關于時間離散的交替迭代問題。

如圖8 所示，迭代的初始狀態T0為距離注漿孔一定范圍內（半徑R0），漿液擴散鋒面為半圓形。通過初始擴散鋒面，可求解該時刻的各個扇形離散單元的鋒面擴散速度，進而求解漿液擴散半徑增量。

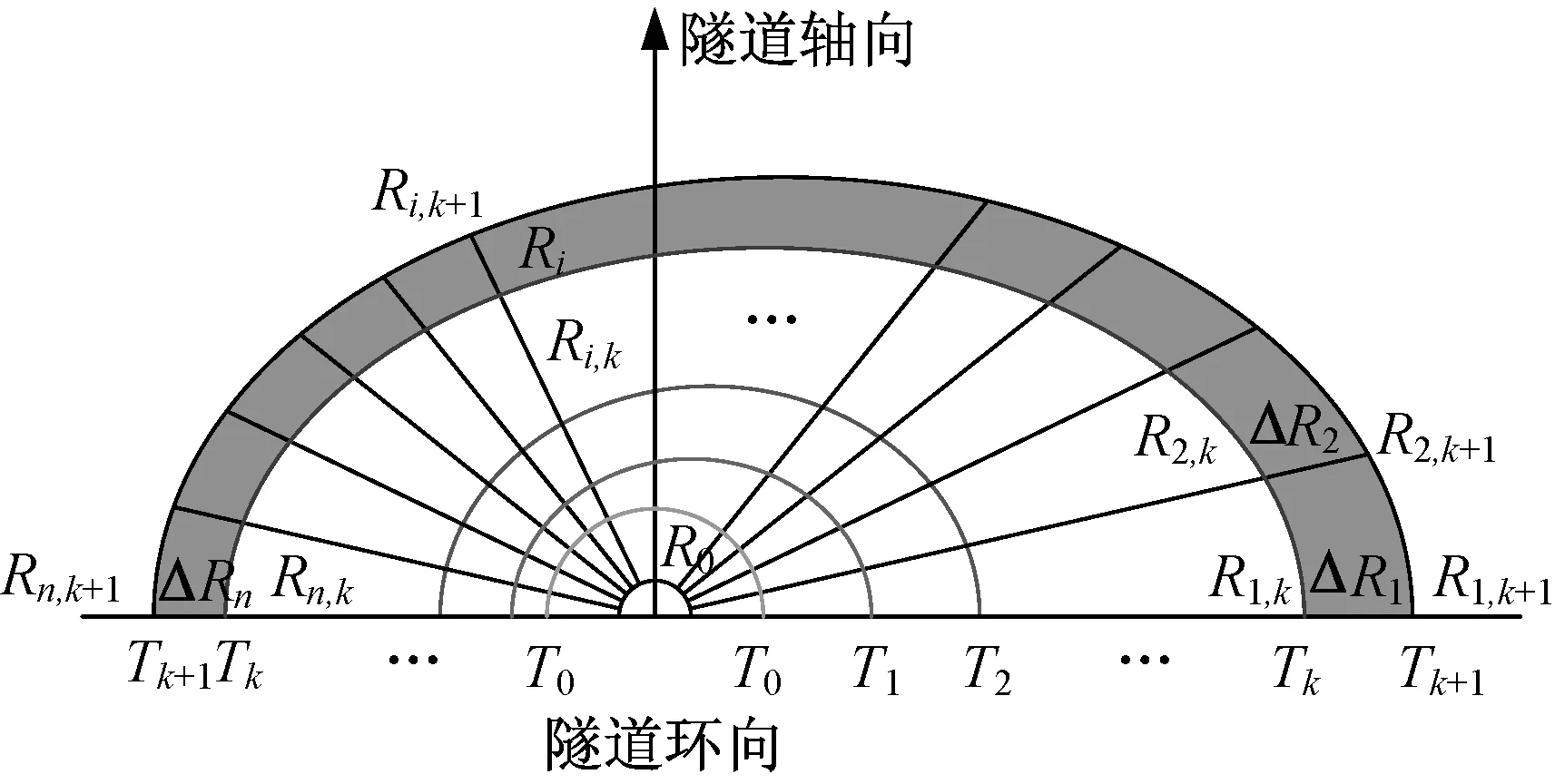
圖8 漿液擴散鋒面步進式求解示意圖Fig.8 Step-wise solution of grout diffusion edge

第Tk+1的擴散鋒面計算公式如下：

式中：vˉi，k為第k時刻第i個扇形單元鋒面處的平均流動速度；ΔRi為第i個扇形單元的流動路徑增量。為保證計算精度，限制max(ΔRi)＜0.1m，因此時間增量ΔTk是可變的。

擴散鋒面疊加擴散半徑增量可得新的擴散鋒面，繼續下一輪計算。循環交替，可以獲得漿液最終收斂狀態下的擴散形態和壓力分布情況。

2.4 數值算法計算流程

盾尾同步注漿算法流程如圖9 所示，計算程序采用MATLAB編寫，具體計算步驟如下：

（1）輸入計算參數，其中幾何參數包括隧道外徑Rt、盾構間隙厚度w，施工參數包括注漿孔的豎向夾角α1、注漿壓力P1以及注漿孔對應埋深處的環境壓力Pd，計算參數包括擴散區域離散參數n 和m（圖6），注漿孔等效半徑r0，初始擴散半圓半徑R0以及計算時步大小Δt；

（2）根據初始半圓擴散鋒面，對漿液擴散區域進行離散；

（3）基于弦截法，給定第i 個扇形單元的注漿流量兩個初始迭代解，計算該扇形單元每個離散環形單元前后的壓力差；

（4）比較前后兩個解的差異性，判斷是否達到誤差要求，進行下一次弦截法迭代；

（5）對所有扇形單元進行注漿流量迭代計算后，得到新的擴散鋒面位置；

（6）基于新的擴散鋒面進行新一輪循環計算；

（7）設定一個計算時間最大值tmax，該最大值通過預先試算確定，保證所有注漿孔的漿液擴散區域足夠覆蓋管片環向范圍；

（8）記錄Ri和Δqi，并基于此得到擴散區域內每一個離散點處的漿液壓力。

圖9 算法流程圖Fig.9 Flow chart of algorithm

3 工程實例分析

參考文獻［4］中關于荷蘭Sophia 鐵路隧道的注漿壓力監測數據，對1.3節中的理論公式和2.4節中數值算法進行驗證。

3.1 工程概況

Sophia 鐵路隧道位于荷蘭Rotterdam 東南約20 km處，包含兩條外徑9.5 m，襯砌厚度0.4 m的圓形盾構隧道。試驗點處，兩條隧道間距10 m，隧道頂部埋深14 m。地層情況如下：地表以下首先為12 m厚全新世土層，包含泥炭土（2/3）和黏土（1/3）；其次為10.7 m厚的中密砂土，隧道位于該土層；砂土層下方為泥炭土和粉質黏土層。在隧道試驗截面處，地下水距地表深度約為1 m，隧道頂部的覆土壓力大致為200 kPa。

Sophia鐵路隧道盾構施工采用典型的六孔注漿方案，注漿孔布設以及注漿壓力見表1，其中環境壓力是指上一環管片推進時注入的漿液在穩定之后的壓力值。參考文獻［4］和文獻［13］，環境壓力豎向變化梯度取為15 kPa·m-1，拱頂環境壓力取值為上覆土壓力200 kPa。盾尾間隙厚度為0.16 m，漿液物理力學參數見表2。其中，注漿壓力一般情況下應略大于環境壓力，實際施工中注漿壓力常出現波動，計算中通常取對應工況下的單環推進穩定時的平均值。本文基于文獻［4］中的現場實測數據，選擇測試截面剛脫出盾尾后（此時的實測壓力值最接近真實的注漿壓力值），鄰近注漿孔位置的測試點的漿液壓力局部平穩值作為注漿壓力值。

表1 Sophia隧道注漿孔布置Tab.1 Layout of grouting holes for Sophia tunnel

表2 同步注漿漿液物理力學參數Tab.2 Physical and mechanical parameters of synchronous grouting slurry

3.2 結果驗證

針對Sophia 鐵路盾構隧道，將相關參數代入同步注漿整體擴散模型的數值計算程序中，得到注漿壓力沿管片外壁的分布結果。需要說明的是，漿液在盾尾間隙中填充擴散時，由于刀盤超挖、地層收斂等因素導致盾尾間隙厚度分布不均，此外漿液在與土體的交界面處還會發生泌水、滲流等過程，土體對漿液的阻滯作用與漿液在一般內壁平整的管道中流動時受到的阻滯作用相比復雜得多。因此，盾尾間隙厚度計算參數不宜直接選擇盾尾間隙理論值，應當進行折減以考慮地層交界面對漿液流動的復雜阻滯作用。文獻［4］漿液壓力監測數據顯示盾尾注漿影響范圍在出盾尾2～3 環內，對應的折減系數可取為50%。

根據表1 所述的注漿壓力和環境壓力值，計算試驗橫截面處的漿液壓力分布，并同現場實測數據進行比較，如圖10所示。

圖10 計算值與實測值對比Fig.10 Comparison between calculated and field values

由圖10 可見，隧道拱頂的漿液壓力實測值為200 kPa，拱底壓力實測值為353 kPa，漿液壓力受漿液自重影響明顯。漿液壓力實測值分布在理論計算值兩側，整體上具有較高的吻合度，同步注漿整體擴散理論模型能夠較好地反映漿液在盾尾間隙充填過程中的壓力分布模式。

3.3 結果分析

文獻［8］中提出的同步注漿充填壓力環向分布模型假定漿液沿著三維環狀薄餅擴散，但環狀薄餅空間只是理想化的假定，實際盾構注漿過程中盾尾間隙內并不會出現類似的空間，其厚度參數既沒有經驗取值，也沒有相關試驗研究，取值缺乏依據。而且薄餅厚度參數δ 敏感性極強，對計算結果影響很大。圖11為文獻［8］提出的環向分布模型與本文縱環向整體擴散模型的計算結果對比。當環向分布模型的δ 取值為1.5 和3.0 cm 時，計算結果的最大誤差分別為－12.64%與6.93%，而本文的整體擴散模型則為5.28%。此外，以均方誤差（mean-square error，MSE）作為計算結果偏差程度的評價指標，三條曲線對應的MSE 分別為398.94（環向分布模型δ=1.5 cm）、196.49（環向分布模型δ=3.0 cm）和69.40（整體擴散模型）。可以看出，環向分布模型的準確性十分依賴δ的正確取值，取值不同，計算結果曲線差異很大。因此，薄餅厚度參數δ 成為了制約環向分布模型應用的因素。而整體擴散模型假設條件較少，不存在薄餅厚度參數δ，其更真實地反映漿液在間隙中的流淌規律，其計算結果也更加精確。

圖11 不同模型計算結果對比圖Fig. 11 Comparison of calculation results of different models

此外，同步注漿整體擴散模型的計算結果可以得到注漿范圍內任一點的漿液壓力。由于計算結果左右對稱，本文僅取右半部分進行分析。圖12分別為注漿孔1，2，3，4 同時注漿時的擴散壓力展開云圖，其中橫坐標表示沿著管片外壁的弧長，其值為0表示隧道頂部，數值隨著順時針旋轉增大，其值為14.92 m表示隧道底部；縱坐標表示沿著隧道軸線的距離，其值為0 表示盾尾所在橫截面，距離盾尾越遠，數值越大；云圖表示漿液壓力的分布情況，單位為kPa；圖中橫軸上的圓環表示注漿孔位置。從圖中可以看出，隧道頂部和底部區域由于管片外壁較為平坦，重力影響不明顯，漿液壓力變化幅度較小，而且由于漿液粘滯阻力的影響，距離注漿孔較遠范圍內漿液壓力小于注漿壓力值；而在拱肩和拱腰處，管片外壁切線與豎向夾角較小，重力對漿液壓力的變化起控制作用，因此等高線在距離注漿孔一定距離后幾乎與隧道軸向平行。

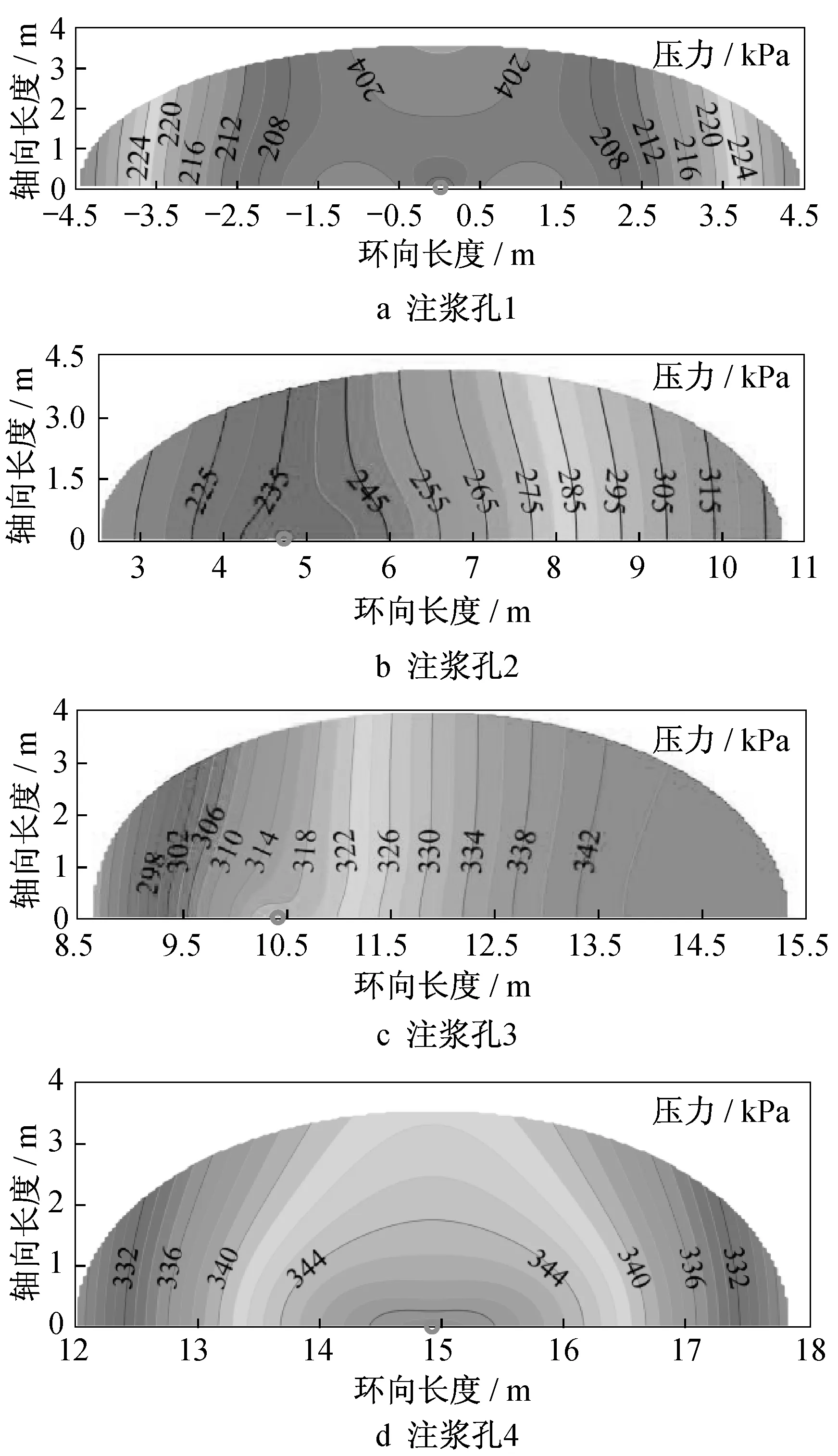
圖12 注漿孔單孔擴散壓力分布云圖Fig.12 Contour of diffusion pressure for single grouting

基于不同注漿孔注入的漿液在交匯面處漿液壓力相等的原則，對4個注漿孔的計算結果進行整合，得到整個管片外壁右半部的漿液擴散壓力分布展開云圖，如圖13所示。將漿液擴散壓力投射到半圓柱形管片外壁，可以直觀地觀察到漿液擴散壓力的起伏情況，如圖14所示。從圖14可以看出，拱頂部位，漿液壓力由于粘滯阻力的影響，出現明顯的下凹區，而注漿孔附近會出現一定范圍的上凸區。網格的顏色也體現了漿液壓力的相對大小，結合圖13，可以看出注漿壓力整體上呈現著上小下大重力主導的趨勢，豎向梯度約為16 kPa·m-1，而在注漿孔附近局部區域漿液壓力分布較為復雜，與注漿孔位置，漿液流動方向以及注漿壓力與環境壓力之間的壓力差等因素有關。在盾構正常推進過程中，注漿孔在未發生堵塞時，注漿壓力只會略高于外界環境壓力。因此，漿液壓力的整體豎向梯度與3.1節中的環境壓力的分布梯度會近似一致。

圖13 同步注漿整體擴散展開云圖Fig.13 Contour of overall diffusion pressure

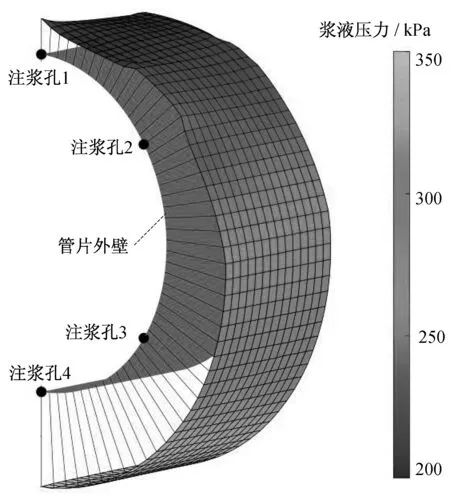
圖14 漿液壓力立體網格云圖Fig.14 Stereoscopic mesh and contour of grout pressure

圖15 為注漿孔處漿液沿著隧道軸線縱向擴散時的壓力衰減曲線，可以看出在距離注漿孔較近區域內，壓力衰減速度較快，而距離注漿孔一定范圍內，壓力趨于平緩。呈現這種壓力衰減規律的原因是因為漿液由注漿孔注入后，漿液的流動速度較大，因此受到的粘滯阻力也比較明顯，隨著漿液的后續擴散，漿液的流動速度逐漸減小，壓力衰減的梯度也隨著減緩。

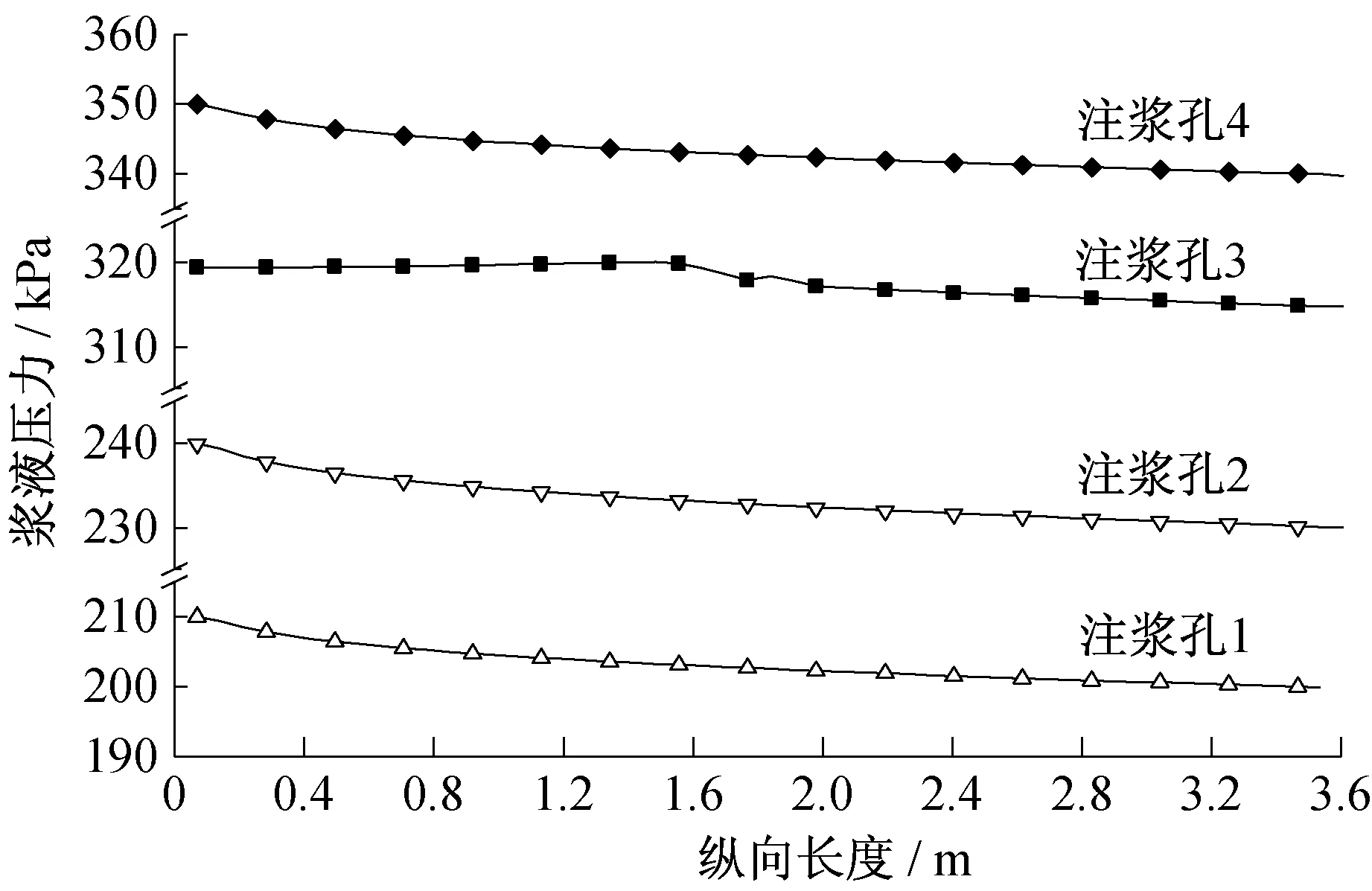
圖15 漿液壓力縱向擴散衰減曲線Fig.15 Longitudinal diffusion attenuation curve of slurry pressure

4 結論

本文通過分析盾尾同步注漿填充擴散機理，改進了現有的盾尾同步注漿擴散模型中漿液縱、環向流動相互獨立的假設條件，將漿液的擴散視為縱環向相互關聯的流動模式。此外，盾尾同步注漿施工通常以注漿量或注漿壓力作為控制參數。但注漿量控制更多地被認為是一種二次被動反饋控制方式，在盾構機轉彎和升降階段中超欠挖時或者遇到復雜地質情況時（諸如裂隙分布較多，存在巖溶空洞），往往無法有效填滿建筑空隙。而注漿壓力控制能更好地適應周圍土層環境壓力的變化，實時調節盾尾注漿流量，減小地層擾動和環境影響。因此，本文以注漿壓力為同步注漿控制參數，通過理論推導和數值算法設計得到了盾構隧道同步注漿縱環向整體擴散理論模型和計算程序，并進行了工程實例分析，得到結論如下：

（1）基于Bingham流體本構模型，考慮漿液縱環向關聯整體擴散運動，以注漿壓力為控制參數，環境壓力為邊界條件，得到了盾尾同步注漿漿液壓力空間分布理論模型。

（2）以壓力為邊界條件，考慮重力影響，漿液在盾尾間隙內的擴散范圍以及擴散鋒面形態為不規則環狀。基于時空離散的概念，對擴散區域進行離散化，通過構造離散網格節點的平衡方程組，求解注漿壓力與漿液擴散半徑（漿液擴散鋒面）的關系式，進而建立了求解盾尾同步注漿范圍內任一點的漿液壓力的數值算法。

（3）盾構隧道同步注漿縱環向整體擴散模型相較于環形分布模型，改進了假定條件，不需引入環餅厚度等敏感假定參數，更加貼近工程實際情況。

（4）工程實例分析表明漿液壓力整體上呈現著上小下大重力主導的趨勢，豎向梯度約為16 kPa·m-1，而在注漿孔附近局部區域漿液壓力分布較為復雜，與注漿孔位置、漿液流動方向以及注漿壓力與環境壓力之間的壓力差等因素有關。同步注漿整體擴散理論模型能夠較好地反映漿液在盾尾間隙充填過程中的壓力分布模式。