一種基于數據融合的全輪驅動車輛質心側偏角估計方法

張征, 劉春光, 馬曉軍, 張運銀

(陸軍裝甲兵學院 兵器與控制系， 北京 100072)

0 引言

質心側偏角是表征車輛運動狀態的主要參數之一，準確獲取質心側偏角也是車輛主動安全研究的一個關鍵內容[1]。由于使用雙軸向非接觸車速測量儀等儀器的測量成本很高，所以質心側偏角一般很難直接獲取，為兼顧成本和精度，通常采用運動學或動力學方法建立狀態觀測器進行估計[2]。

有學者使用信號積分法估測車輛質心側偏角，這種方法由于信號長時間積分，容易造成很大的累積誤差，目前，積分法已經很少單獨使用[3-4]。一些學者將車輛動力學模型和非線性輪胎模型引入狀態觀測系統，運用擴展卡爾曼濾波、無跡卡爾曼濾波(UKF)和粒子濾波等算法對質心側偏角進行估計[5-7]。擴展卡爾曼濾波算法通過忽略泰勒級數高階項，對模型進行了線性化處理，導致該算法在一定程度上降低了車輛狀態參數估計的精度[8]。UKF算法能夠減小一部分由于模型線性化引起的誤差，并且實時性較好，是一種較為常用的濾波算法，但這種方法容易受到環境中的非高斯噪聲干擾，影響估計效果[9]。粒子濾波算法能夠比較準確地假定系統噪聲，但該算法存在粒子退化、計算量大等問題，不利于工程應用[10]。

針對上述問題，本文將某型8輪電驅動車輛作為研究對象，結合全輪電驅動車輛系統多信息源、強非線性的特點，提出了一種基于數據融合的質心側偏角估計方法。建立了非線性3自由度車輛模型和輪胎模型，運用UKF算法設計了質心側偏角估計器。同時，為進一步改善UKF算法易受干擾問題，采用信號積分法估計質心側偏角，并基于多元函數求極值理論，計算出總均方誤差最小時所對應的加權因子，然后將UKF算法和信號積分算法進行數據融合，以提升車輛行駛狀態參數估計效果。最后，在基于實車中央控制器的實時仿真平臺上進行了不同行駛工況下的車輛狀態參數估計仿真。

1 質心側偏角估計結構及原理

為全輪驅動車輛設計了一種基于數據融合的質心側偏角估計器。車載傳感器采集到橫擺角速度、橫/縱向加速度、輪速等信號后，與電機輸入信息、路面附著系數及駕駛信號一同作為輸入端信息，分別運用UKF算法和信號積分算法對車輛質心側偏角進行估測，然后通過最小方差加權平均法，將兩種算法計算出的估計值進行數據融合，得出最終質心側偏角估計結果。具體結構如圖1所示。

圖1 質心側偏角估計器結構圖Fig.1 Block diagram of sideslip angle estimator

2 車輛動力學模型建立

圖2 非線性3自由度車輛模型Fig.2 3-DOF nonlinear dynamics model of vehicle

全輪驅動車輛行駛時，容易出現較頻繁的加減速和轉向運動，而常用的單軌2自由度模型一般難以滿足車輛狀態參數估計需求[11]。為適應研究對象復雜多變的越野機動環境，建立非線性3自由度車輛模型。所建模型如圖2所示。圖2中：v為車輛速度；vx和vy分別為縱向車速和側向車速；γ為橫擺角速度；β為質心側偏角；Fxij、Fyij(i=1，2，3，4為第i軸，j=1，2為左側和右側)分別為縱向力、側向力；δij為車輪的轉向角；αij為車輪的側偏角；l為輪距；Li為第i軸距離質心O處的距離。

建立車輛動力學方程

(1)

式中：Iz為繞質心O的轉動慣量；ax和ay分別表示縱向車速加速度和側向車速加速度。

(1)式變化后，得到如下表達式:

(2)

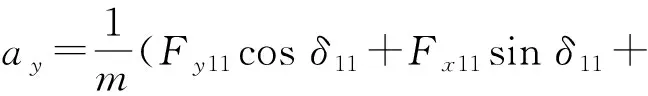
(3)

(4)

式中：m為車輛質量。

輪胎縱向力Fxij計算如下：

(5)

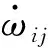
驅動力矩Tij可通過電機輸入信息獲得，即

Tij=Te,ijig,

(6)

式中：Te,ij為輪轂電機提供的力矩；ig為減速比。

車輛側向運動受到輪胎側偏力的支配影響，本文采用半經驗公式的Pacejka輪胎模型對輪胎力進行計算，表達式一般形式為

Fy=Dsin {Carctan[Bαij-E(Bαij-arctanBαij)]},

(7)

式中：D為輪胎模型峰值系數；C為形狀特性系數；B為剛度系數；E為曲率系數。根據文獻[12]，通過參數擬合計算得到系數D、C、B和E.

各輪側偏角可近似表達為

(8)

3 無跡卡爾曼濾波器設計

在車輛動力學模型基礎上，對非線性狀態空間進行描述，建立UKF算法的狀態方程和量測方程，并設計車輛質心側偏角非線性估計器。

3.1 狀態估計模型

建立車輛狀態參數估計狀態方程和量測方程，并進行離散化處理，即

(9)

式中：下標k和k+1分別為k和k+1采樣時刻；Xk+1和Xk分別為第k+1和k時刻狀態變量；zk+1為第k+1時刻量測變量；u為輸入向量；qk、rk分別為0均值，且協方差為Q、R的過程噪聲、量測噪聲。

狀態變量X=[β,γ,vx]T，本文著重分析β的估計結果；輸入向量u=[δ11,δ12,δ21,δ22,Tij]T；量測變量z=[ax,ay,γ,ωij]T，其中ωij為各車輪的轉速。

3.2 UKF算法設計

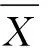
(10)

2n+1個Sigma點權值為

(11)

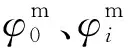
初始條件為

(12)

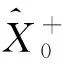
狀態變量進行無跡變換，Sigma點預測值為

(13)

Sigma點預測值加權后，X的預測值及其誤差的協方差矩陣為

(14)

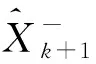
(15)

(16)

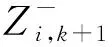
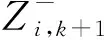
(17)

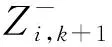
計算量測量協方差為

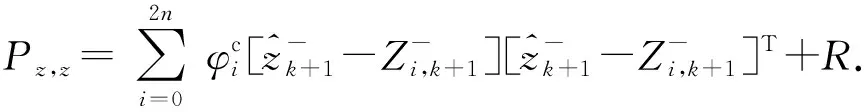
(18)

X與z間協方差的關系可為

(19)

卡爾曼增益為

Kk+1=Pz,z[PX,z]-1.

(20)

更新得

(21)

4 數據融合方法設計

全輪驅動車輛行駛條件復雜，甚至需要面臨小半徑滑移轉向、輪胎大側偏等特殊工況，當車輪發生較大側偏時，特別是當vx(k)γ(k)=0時，使用UKF算法估計出的質心側偏角精度將難以保證，因此需要結合信號積分法進行估測，其表達式為

(22)

(21)式積分并進行離散化處理：

(23)

式中：Δt為離散化采樣時間。兩種估計算法進行數據融合，根據道路情況(路面附著系數μ)和加速/制動踏板開度ρ(-1≤ρ≤1)對車輛行駛工況進行劃分[14]，行駛工況Apq(p=1,2,3且q=1,2,3)的對應區域如表1所示。

表1 車輛運行工況劃分

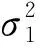
兩種估計算法的加權平均結果為

x(k)=ξ1x1(k)+ξ2x2(k),

(24)

式中：ξ1∈[0,1]和ξ2∈[0,1]分別為UKF算法和信號積分算法在質心側偏角估計融合算法中所占權重值。

并且，加權系數存在如下關系：

ξ1+ξ2=1.

(25)

因此，兩種估計算法計算結果經加權平均后可以得到真實信號的無偏估計。

由于x1(k)和x2(k)數據間相互獨立，并且為真實值的無偏估計，因此存在：

E[(x-x1)(x-x2)]=0.

(26)

由此可得均方誤差表達式為

(27)

根據柯西不等式及權值的定義[15]，有

(28)

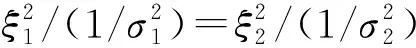
基于多元函數求極值理論，可求出總均方誤差最小時所對應的加權因子，即

(29)

此時，對應的最小均方誤差為

(30)

(31)

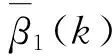
5 仿真結果及分析

由于研究對象全輪驅動車輛的樣車尚未生產，因此在硬件在環實時仿真平臺上，進行車輛狀態參數估計仿真驗證。實時仿真平臺由駕駛員操控艙，以實車中央控制器為核心的綜合控制系統，基于系統實時仿真平臺軟件包RT-LAB的電機驅動系統及綜合電力系統，和基于動力學仿真Vortex軟件的系統構成，各系統間采用 Flexray 總線通信。進行仿真時，將所設計的質心側偏角估計算法轉換為代碼，導入實車中央控制器，然后再將中央控制器并入仿真系統，就可以模擬車輛實際運行環境，實現硬件在環仿真。平臺具體結構如圖3所示。

圖3 硬件在環實時仿真平臺Fig.3 Hardware-in-loop real-time simulation platform

為驗證所提出方法在不同行駛工況下的質心側偏角觀測效果，設計高附著路面蛇形行駛、低附著路面雙移線行駛、變附著路面變速連續轉彎行駛3種工況。Vortex動力學仿真系統反饋的車輛質心側偏角信息可作為質心側偏角跟蹤值。

具體仿真條件設定如下：

1)高附著路面蛇形行駛：在μ=0.8的路面進行蛇形路段行駛，油門踏板給定ρ=0.5. 采集的信號和估計結果圖4所示。

2)低附著路面雙移線行駛：在μ=0.3的路面進行雙移線行駛，油門踏板給定ρ=0.8，采集的信號和結果如圖5所示。

3)對接路面連續轉彎行駛：在變附著系數路面進行變速連續轉向行駛。前10 s油門踏板給定ρ=0.5，后10 s油門踏板給定ρ=0.8，結果如圖6所示。

圖4為車輛在高附著路面運動時，駕駛員對方向盤操縱信號、橫擺角速度信號及質心側偏角估計結果，從中可以看出：使用UKF算法和融合算法計算出的質心側偏角估計值與Vortex仿真反饋的跟蹤值之間均具有很好的一致性，但數據融合算法估計值比UKF算法估計值更趨近于仿真跟蹤值。

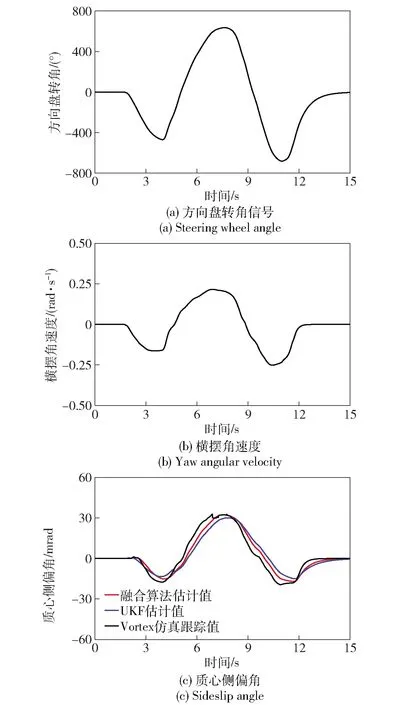
圖5 低附著路面雙移線工況Fig.5 Double shifting on low adhesion road

根據圖5可知：當路面附著系數較低時，在整體趨勢上，UKF算法的估計值與仿真跟蹤值基本保持一致，但當側向運動相對劇烈時，尤其是質心側偏角曲線的“波峰”和“波谷”處，估計值和仿真跟蹤值間存在明顯誤差；而采用融合算法估計質心側偏角時，整體誤差都很小，即使在質心側偏角變化比較大的情況下也能保持良好的跟蹤效果。

從圖6可以看出：UKF算法和數據融合算法均能對質心側偏角進行有效估計，但在路面附著系數和油門踏板信號發生變化時，單一算法的適應性較差，估計精度不夠理想；而融合算法在整個行駛過程中均保持了較好的估計精度，特別是在復雜工況下的估計效果明顯優于單一算法。

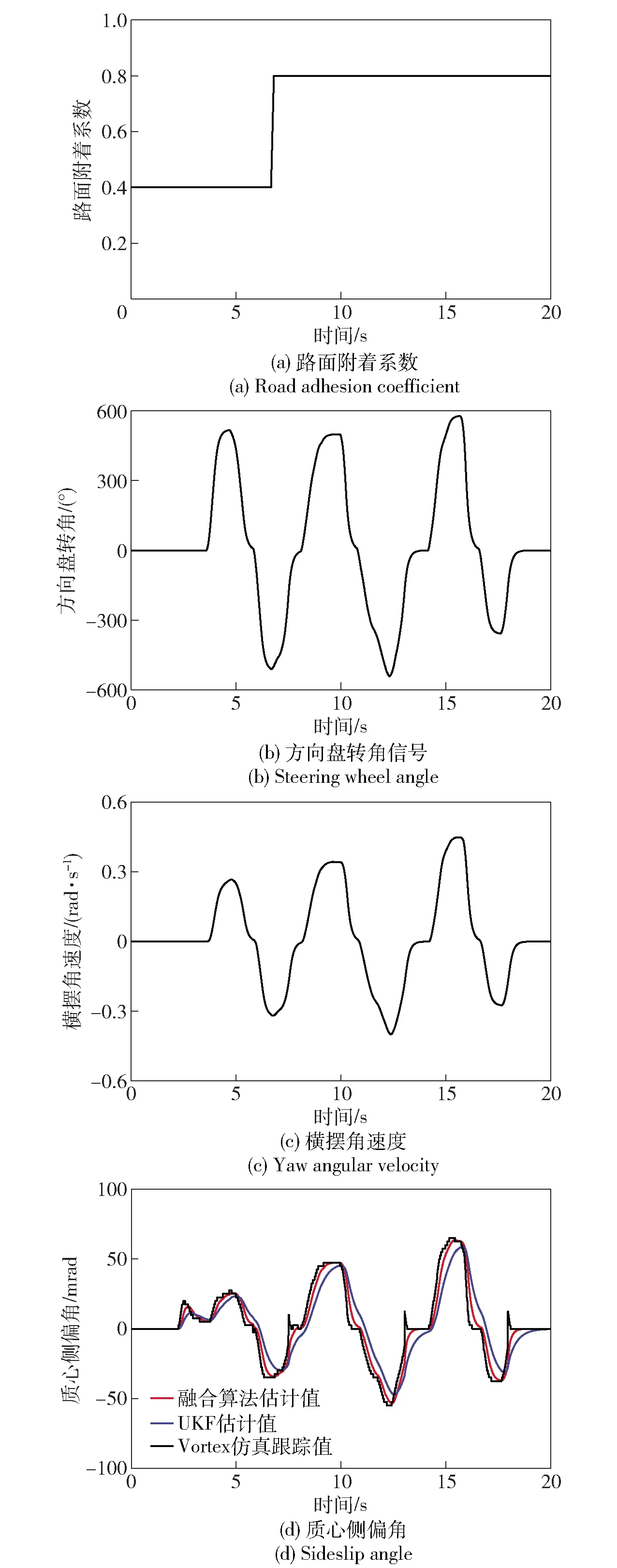
圖6 變附著路面連續轉向工況Fig.6 Continuous steering on variable adhesion road

表2將UKF算法和融合算法產生的質心側偏角估計誤差進行了對比，根據誤差統計數據可以看出：高附著路面蛇形行駛工況下，采用UKF算法、融合算法所產生的最大誤差分別為22.51 mrad、13.63 mrad，均方根誤差分別為2.03 mrad和0.92 mrad；在低附著路面、車輛雙移線行駛工況下，兩種算法的最大估計誤差分別為11.95 mrad和6.32 mrad，均方根誤差分別為1.08 mrad和0.53 mrad；在對接路面、車輛進行變速連續轉向行駛時，兩種算法的最大估計誤差分別為33.81 mrad和16.59 mrad，均方根誤差分別為3.73 mrad和1.26 mrad. 由此可以看出，后者的質心側偏角估計精度優于前者，這驗證了融合算法在車輛不同行駛工況下都具有良好的估計效果。

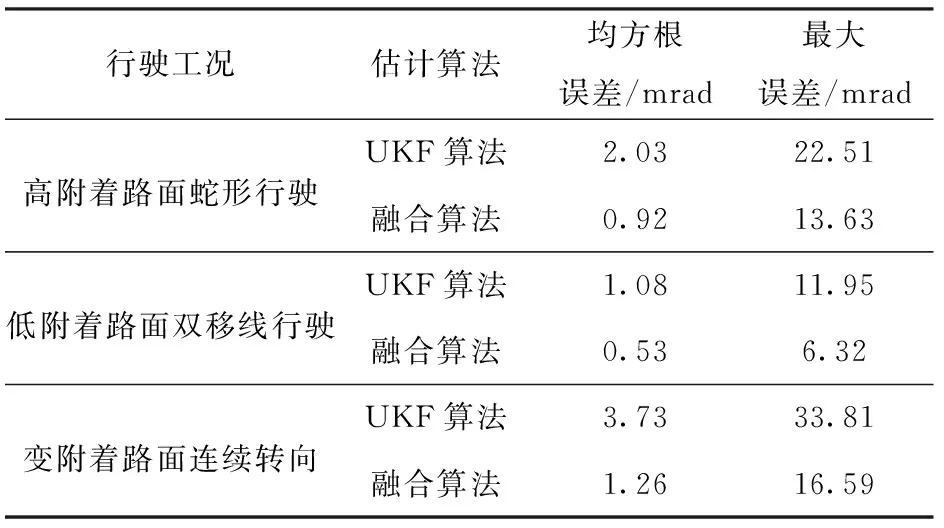
表2 質心側偏角估計誤差統計表

6 結論

1)本文根據全輪驅動車輛特點，設計了基于UKF和信號積分數據融合的質心側偏角估計方法。結合非線性3自由度車輛模型，采用UKF算法建立了行駛狀態參數估計方程。此外，運用了信號積分法估計車輛質心側偏角，并根據車輛行駛工況，基于總均方誤差最小的原則，將兩種算法計算出的估計值進行了數據融合，盡量減小了算法復雜度和計算時間的增加，得到了最終的質心側偏角估計結果。

2)采用硬件在環實時仿真平臺設計并完成了質心側偏角估計仿真驗證。結果表明，所提出的數據融合方法能夠實時、準確地估計出車輛不同行駛工況下的質心側偏角，有效解決了單一行駛狀態參數估測方法適用范圍局限的問題，改善了車輛質心側偏角的估計效果，為全輪電驅動車輛狀態參數估計和下一步的操縱穩定性控制研究提供了一個新的思路。