地區人力資源對人均GDP的作用機理研究
——基于武漢市數據
呂小柏,李 釗
(武漢科技大學管理學院,武漢 430081)
前人從資源角度對人力資源的研究由來已久,研究也相當充分;從經濟角度對勞動生產率、人力資本等要素的研究也比較充分,如學者孫浦陽的研究[1];從區域經濟角度探討經濟發展與就業、人口狀況、人力資本及社會穩定的關系的研究也不少,如學者張智敏的研究[2]、郭凱明的研究[3],等等.但比較少見的是將人力資源—經濟發展的源頭與人均GDP—經濟發展的結果相聯系的研究.
人均GDP是衡量一個地區經濟發展水平的常用指標,也是基礎性指標.人力資源作為基礎的資源要素支撐著地區經濟的發展.研究人力資源與人均GDP之間的關系,搞清楚它們是如何發生作用的,本研究認為很有必要.只有明白了兩者間的作用機理才能在區域管理中有的放矢,少走彎路.
武漢市是我國中部最大的城市,有著復雜的經濟系統和多元的經濟結構,承擔著國家發展的戰略任務.選取武漢市數據作為研究素材,一是因為其統計數據較為完整連續,便于做定量分析,二是因為其復雜的經濟體系及人力資源狀況具有代表意義.本研究所用數學工具及方法均來自李紅松、鄧旭東主編的《統計數據分析方法與技術》[4].
1 研究指標
1.1 選取研究指標
一個地區的地區生產總值(Gross Domestic Product,GDP)是公認的衡量該地區經濟社會發展的最重要的經濟指標,本研究從人均GDP入手,分層構建分析指標,并利用Eviews 9.0軟件和武漢市二十五年的統計數據做定量定性分析,探究一個地區的人力資源對人均GDP的作用機理.本研究所用數據均取自《武漢市統計年鑒》.
依照人均GDP的含義將其進行如下分解:
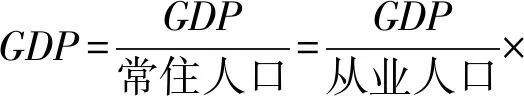
(1)

人均GDP=勞動生產率×就業率×
勞動適齡人口率=LP×LU×WR.
(2)
公式(2)將人均GDP這一基礎指標分解為LP、LU、WR三個二級分析指標,而這三個指標都是人力資源相關指標,(2)式將經濟指標與人力資源指標關聯起來.本研究以公式(2)為主線,通過分析武漢市勞動生產率、就業率和勞動適齡人口率三項指標與人均GDP的關系展開研究.
1.2 確定分析變量
根據前人的研究和相關理論的敘述,并考慮實際需要,本研究將LP、LU、WR三個指標的影響因素做了概括并認為,影響LP的因素主要有產業集聚、資本深化、產業結構、工資水平等;影響LU的因素主要有工資水平、宏觀經濟狀況、產業結構、人口結構等;而影響WR的主要因素有戶籍適齡人口數量和常住外來人口數量.
具體地,產業集聚因素用產業密度(industry density)來表示,即各產業就業人數與武漢市城市面積之比,其中,第一產業、第二產業和第三產業的產業密度本研究分別表示為ID1、ID2、ID3.資本深化因素用勞均投資(investment per worker)來表示,即總投資額與勞動人口數量之比表示為IPW.產業結構(Industry Structure)因素用各產業產值占城市總產值的比例來表示,第一產業、第二產業、第三產業的結構因素分別表示為IS1、IS2、IS3,因為有IS1=1-(IS2+IS3),所以本研究只需取IS2和IS3兩個變量.工資水平因素用城鎮非私營單位年均工資表示,并用城鎮居民消費價格指數將名義平均工資調整為實際平均工資(real average wage)表示為RAW.宏觀經濟狀況因素用地區生產總值的增長率(growth rate)來表示即GR.
本研究認為人口結構因素由兩個變量構成,即戶籍勞動適齡人口(registered working-age population)RWAP和外來勞動適齡人口(immigrant working-age population)IWAP.按照我國現行標準,男性16~59周歲,女性16~54周歲為勞動適齡人口.由于統計口徑的偏差,本研究做以下假設:假設武漢市常住外來人口均為勞動適齡人口.這是一種與實際情況近似的假設.雖然外來勞動適齡人口是常住外來人口的一部分,但由于外來人口到武漢市最主要的目的是就業,盡管其中有隨遷的未成年人和退出勞動力市場的老人,但主體部分是勞動適齡人口.在此假設下,外來勞動適齡人口IWAP可以用常住外來人口(immigrant population)即 IP表示,其數據可在《武漢市統計年鑒》上獲得.
本研究所涉及的指標、變量名稱及符號如表1所示.
2 構建分析模型
2.1 勞動生產率LP模型
由本研究2.2知,勞動生產率LP與ID1、ID2、ID3、IPW、IS2、IS3、RAW七個分析變量有關.為了將各分析變量之間的單位差異標準化并減少異方差性,且不改變原分析變量的基本性質,將以上ID1、ID2、ID3、IPW、IS2、IS3、RAW七個分析變量及LP取自然對數,所形成的新變量為lnLP、lnID1、lnID2、lnID3、lnIPW、lnIS2、lnIS3、lnRAW,其中,lnLP為被解釋變量,lnID1、lnID2、lnID3、lnIPW、lnIS2、lnIS3、lnRAW七個變量為解釋變量.

表1 指標、變量名匯總表Tab.1 Names of index and variable
對新變量做單位根檢驗.單位根檢驗主要有Dickey-Fuller檢驗(DF檢驗)和Augmented Dickey-Fuller檢驗(ADF檢驗).由于當隨機擾動項存在自相關時,DF檢驗會出現偏差,因此本研究采用ADF檢驗并運用Eviews 9.0軟件實現.表2是各變量的ADF檢驗結果.
由表2得知,變量lnLP、lnID2和lnRAW為二階單整,變量lnID1和lnIPW平穩,其余變量都是一階單整,因而不能直接做協整檢驗.為了解決單整階數不一致的問題,分別取lnLP、lnID2和lnRAW一階差分,將三個二階單整變量降階為一階單整變量,再次形成的新變量為DlnLP、DLnID2和DlnRAW,而此時變量DlnLP、DLnID2和DlnRAW的實際意義為lnLP、lnID2和lnRAW的增長率.對于變量lnID1和lnIPW,由于ADF檢驗結果顯示為平穩,本研究不再考慮它們對LP的影響.
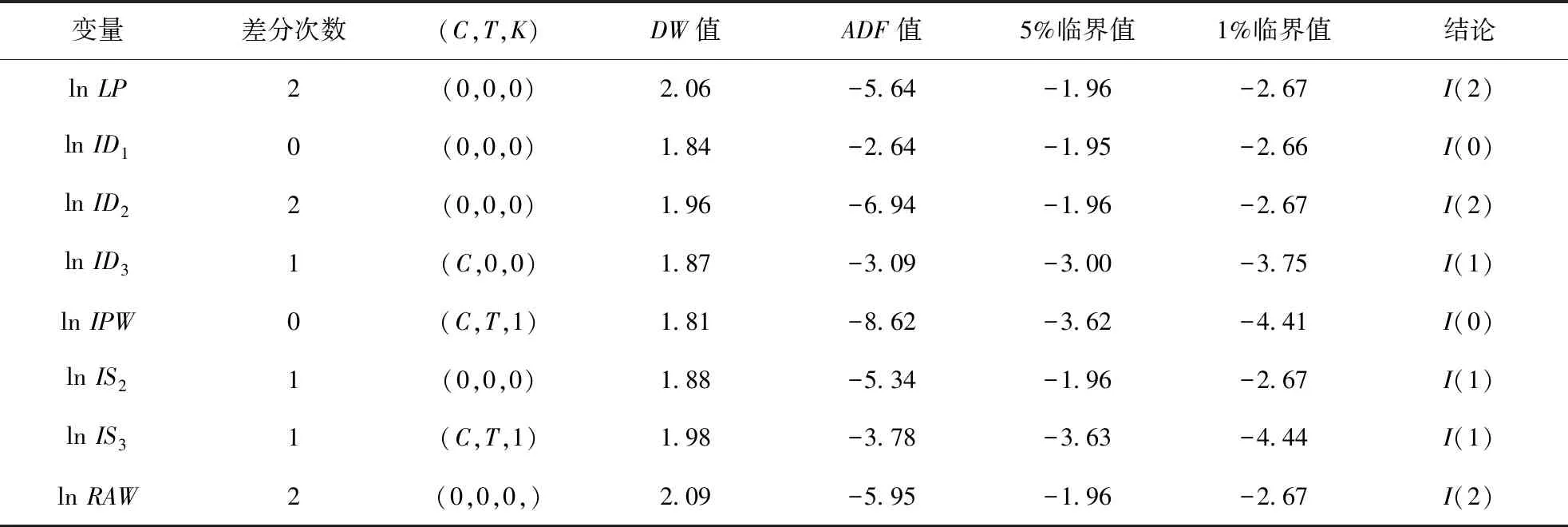
表2 ADF檢驗結果Tab.2 ADF test results
說明:1、(C,K,T)表示ADF檢驗中是否包含常數項、時間趨勢項以及滯后期數;I(n)的括號中表示單整階數,I(0)表示平穩.2.表中的檢驗值均取小數點后兩位,并進行四舍五入.3、結論的得出以5%為臨界水平.以上說明下同.
于是滿足一階單整的變量有被解釋變量DlnLP,解釋變量DlnID2、lnID3、lnIS2、lnIS3和DlnRAW.將這六個變量用Johansen方法進行協整檢驗,選擇有截距無時間趨勢和有截距有隨機時間趨勢的檢驗形式,用Eviews9.0軟件實現檢驗.兩種檢驗形式的跡檢驗和做大特征根檢驗結果均表明,在5%的顯著性水平下,被解釋變量DlnLP和各解釋變量之間均存在三個協整方程.因此說明上述變量之間存在協整關系.
建立回歸方程.本研究采用普通最小二乘法即OLS方法建立回歸模型,并設定為以下形式:
DlnLP=β1+β2DLnID2+β3lnID3+
β4lnIS2+β5lnIS3+β6DlnRAW+μt.
(3)
(3)式中βi為常數項、μt為隨機波動項.
用Eviews 9.0軟件生成DlnLP,DlnID2、lnID3、lnIS2、lnIS3,DlnRAW的OLS回歸模型,得到結果如表3所示.
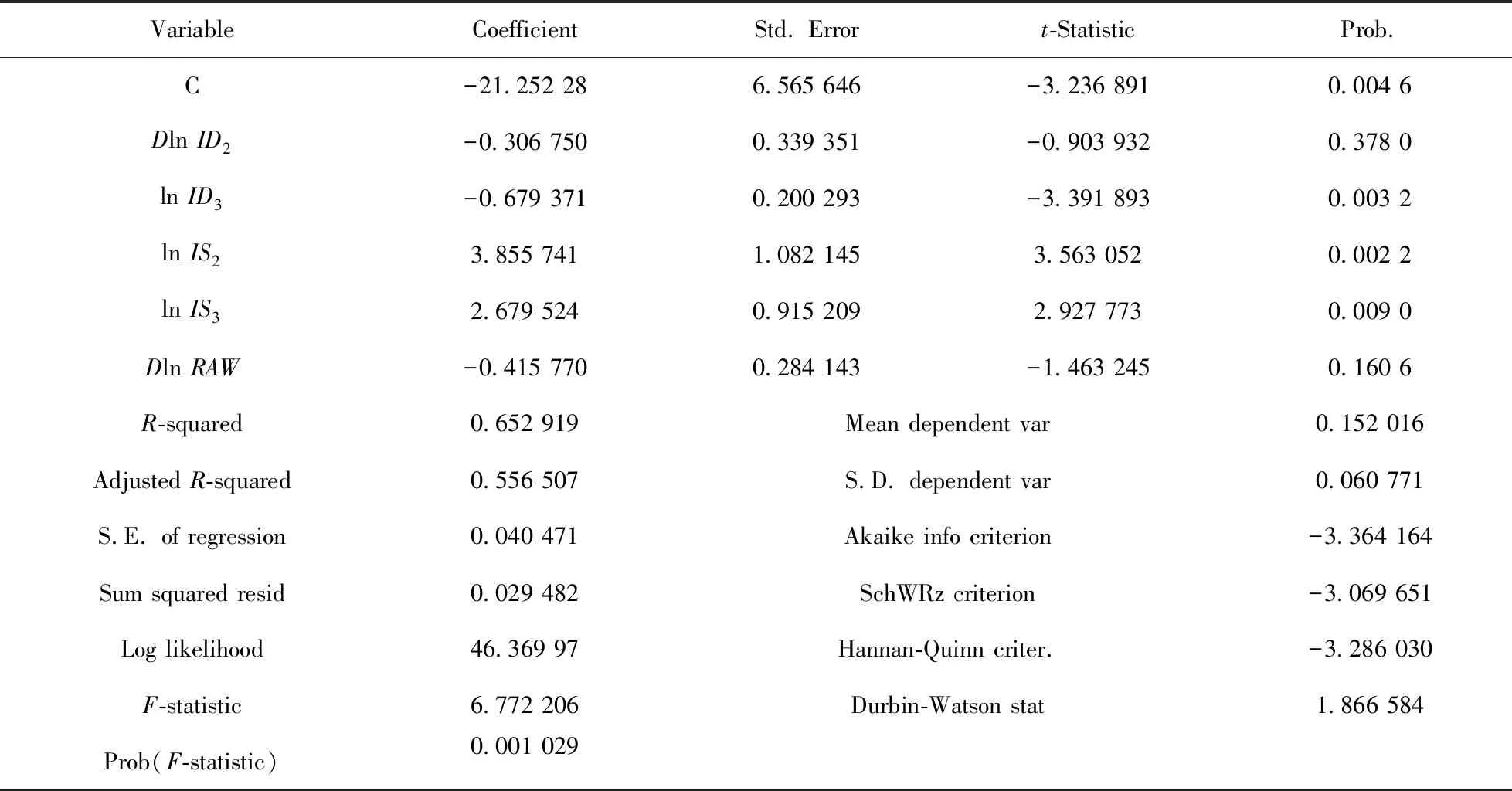
表3 OLS 回歸結果Tab.3 OLS regression results
對表3的回歸結果進行序列自相關的LM檢驗及帶交叉項的White異方差檢驗,檢驗結果表明在5%的顯著性水平下,不存在自相關及異方差.因此,各變量的顯著性系數有效.但表3顯示,DLnID2、DlnRAW的t統計量的伴隨概率(0.378 0、0.160 6)均遠大于0.05,表明它們對被解釋變量DlnLP的影響不顯著,各變量之間可能存在嚴重的多重共線性,采用方差擴大因子法進行進一步檢驗.具體地,將每個解釋變量分別作為被解釋變量都對其它解釋變量進行回歸,得出可決系數R2的值,并依此計算方差擴大因子的數值.檢驗結果如表4所示.
表4顯示,lnID3、lnIS2、lnIS3的方差擴大因子遠遠大于10,表明存在嚴重的多重共線性,這里采用逐步回歸法解決變量的多重共線性問題.在經過一元回歸、二元回歸、三元回歸、四元回歸后,最終滿足要求并被保留的解釋變量有三個,分別為lnIS2、lnID3和lnIS3.
將解釋變量lnIS2、lnID3和lnIS3與被解釋變量DlnLP用OLS進行回歸模型的估計,得到的結果如表5所示.
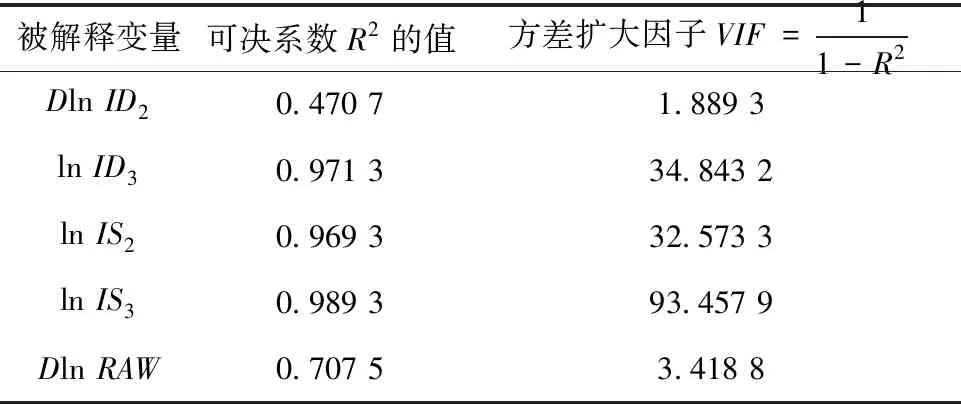
表4 方差擴大因子法檢驗結果Tab.4 Test results of the expanded variance factor method
注:以上數值均為四舍五入后的近似值.下同.
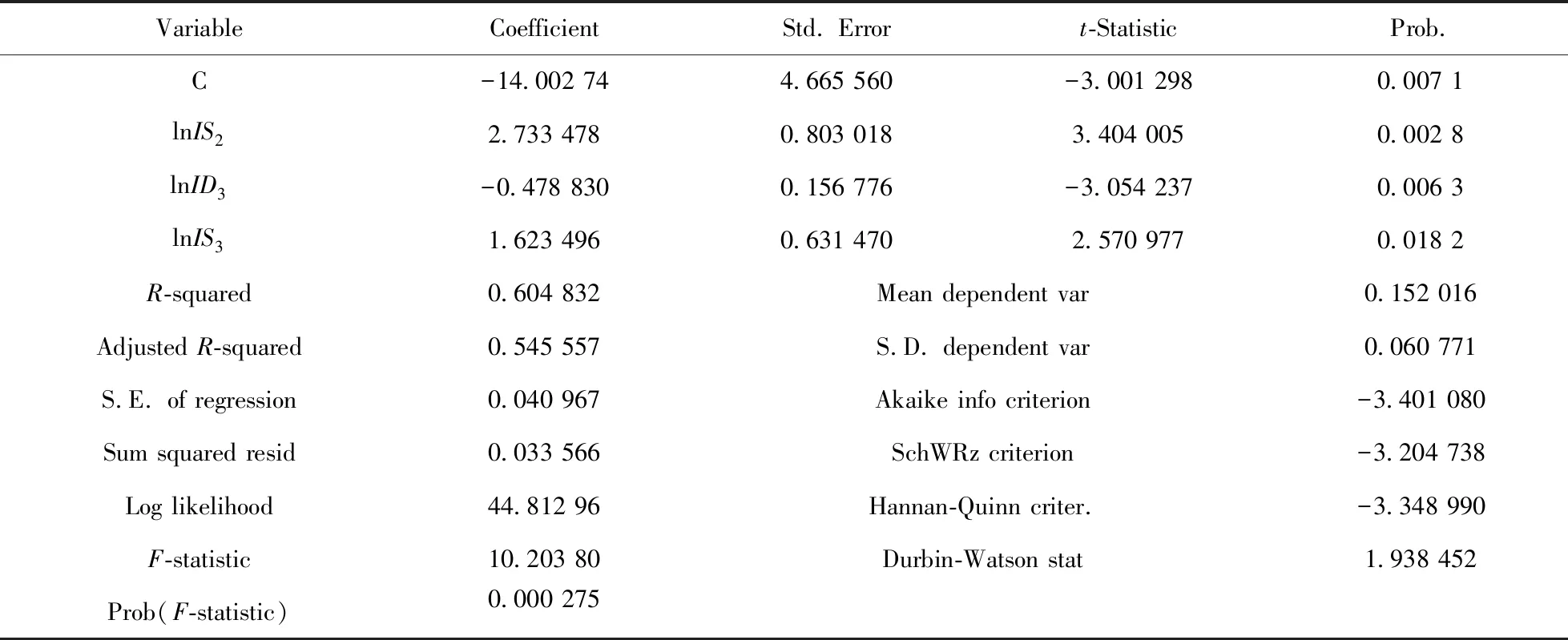
表5 OLS 回歸結果Tab.5 OLS regression results
模型的估計結果為:
DlnLP=-14.0027+2.7335lnIS2+
1.6235lnIS3-0.4788lnID3.
(4)
(4.6656) (0.8030) (0.1568) (0.6315)
t=(-3.0013)(3.4040)(-3.0542)(2.5709)
F=10.2038,DW=1.9385.
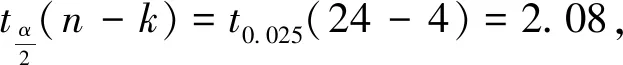
2.2 就業率LU模型
由本研究1.2知,就業率LU與RAW、IS2、IS3、RWAP、IP、GR六個分析變量有關.為了將各分析變量之間的單位差異標準化并減少異方差性,且不改變原分析變量的基本性質,將以上RAW、IS2、IS3、RWAP、IP、GR六個分析變量及LU取自然對數,所形成的新變量為lnLU、lnRAW、lnIS2、lnIS3、lnRWAP、lnIP、lnGR,其中,lnLU為被解釋變量,lnRAW、lnIS2、lnIS3、lnRWAP、lnIP、lnGR六個變量為解釋變量.
對新變量做單位根檢驗.各變量的ADF檢驗結果如表6所示.
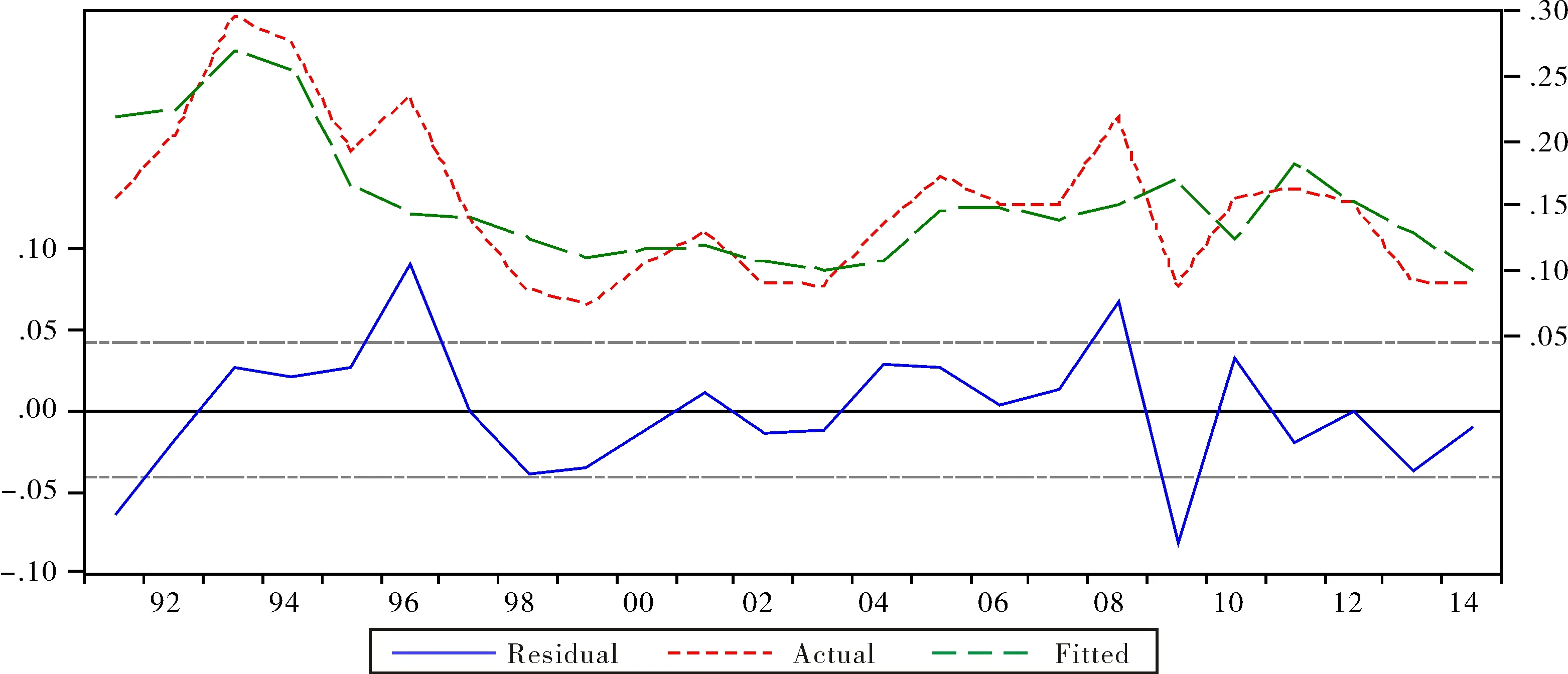
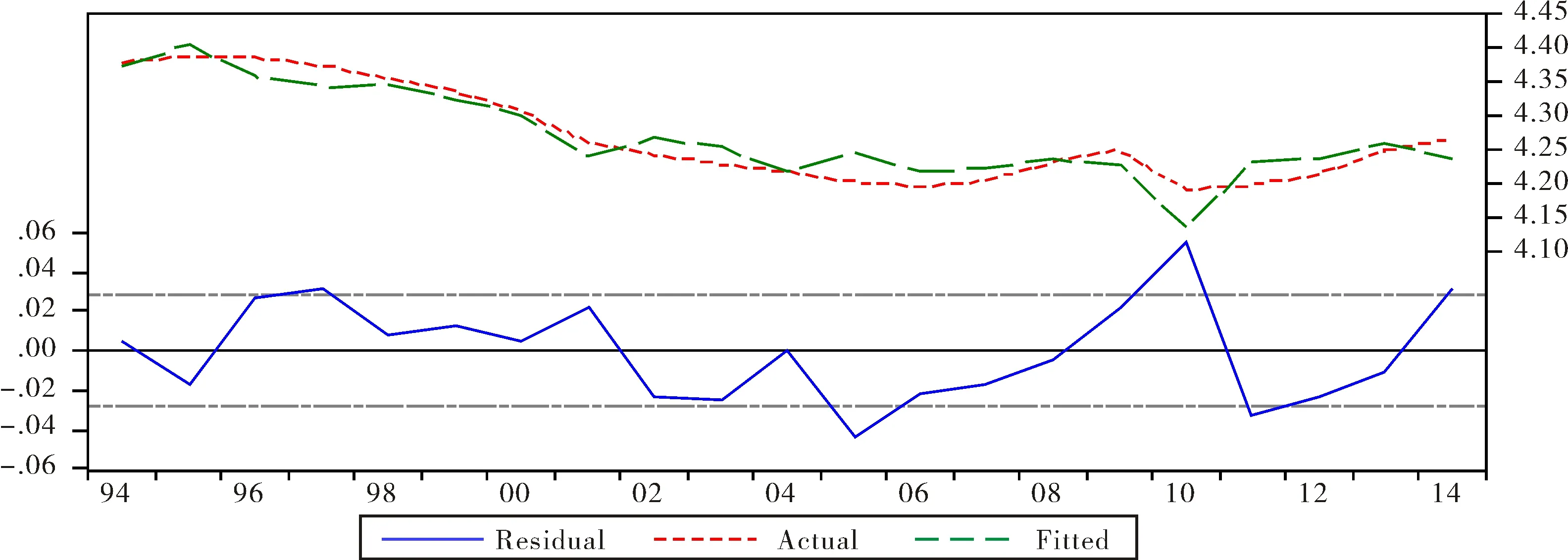
圖1 模型的實際值、擬合值和殘差圖Fig.1 Map of actual value,fitting value and residual
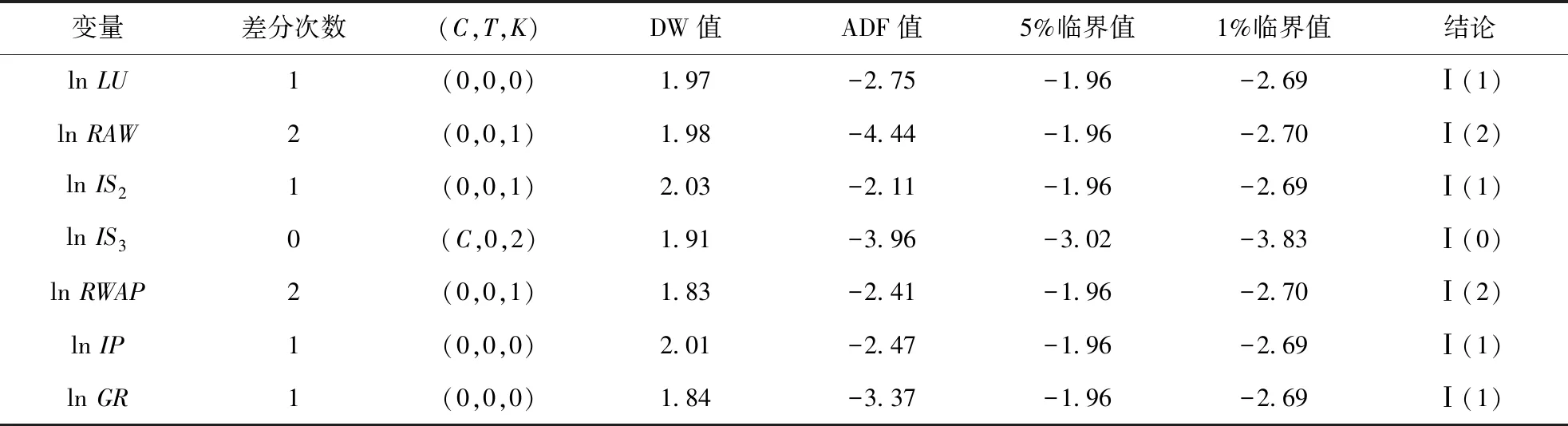
表6 ADF檢驗結果Tab.6 ADF test results
說明:lnRAW、lnIS2、lnIS3的檢驗結果與表2存在差異是由于樣本數量變化所致.
表6顯示,變量lnRAW和lnRWAP為二階單整,變量lnIS3平穩,其余變量都是一階單整,因而不能直接做協整檢驗.為了解決單整階數不一致的問題,分別取lnRAW和lnRWAP一階差分,將兩個二階單整變量降階為一階單整變量,再次形成的新變量為DlnRAW和DlnRWAP,而此時變量DlnRAW和DlnRWAP的實際意義為lnRAW和lnRWAP的增長率.對于變量lnIS3,由于ADF檢驗結果顯示為平穩,本研究不再考慮它對LU的影響.
于是滿足一階單整的變量有被解釋變量lnLU,解釋變量DlnRAW、lnIS2、DlnRWAP、lnIP和lnGR.將這五個變量用Johansen方法進行協整檢驗,選擇有截距無時間趨勢和有截距有隨機時間趨勢的檢驗形式,用Eviews 9.0軟件實現檢驗.在5%的顯著性水平下,有截距無時間趨勢的協整檢驗表明各變量之間至少有五個協整方程,有截距項有隨機時間趨勢的協整變量表明各變量之間至少有六個協整方程,因此說明上述變量之間存在協整關系.
建立回歸方程.采用OLS方法建立回歸模型,并設定為以下形式:
lnLU=β1+β2DlnRAW+β3lnIS2+
β4DlnRWAP+β5lnIP+β6lnGR+μt,
(5)
式中,βi為常數項,μt為隨機波動項.
用Eviews 9.0軟件生成lnLU、DlnRAW、lnIS2、DlnRWAP、lnIP、lnGR的OLS回歸模型,得到的結果如表7所示.
對表7的回歸結果進行序列自相關的LM檢驗及帶交叉項的White異方差檢驗,檢驗結果表明在5%的顯著性水平下,不存在自相關及異方差.因此,各變量的顯著性系數是有效的.但表7顯示,DlnRWAP的伴隨概率(0.134 5)大于0.05%,表明它對被解釋變量lnLU的影響不顯著,各變量間可能存在多重共線性,采用方差擴大因子法做進一步檢驗.各變量的可決系數和方差擴大因子的結果如表8所示.
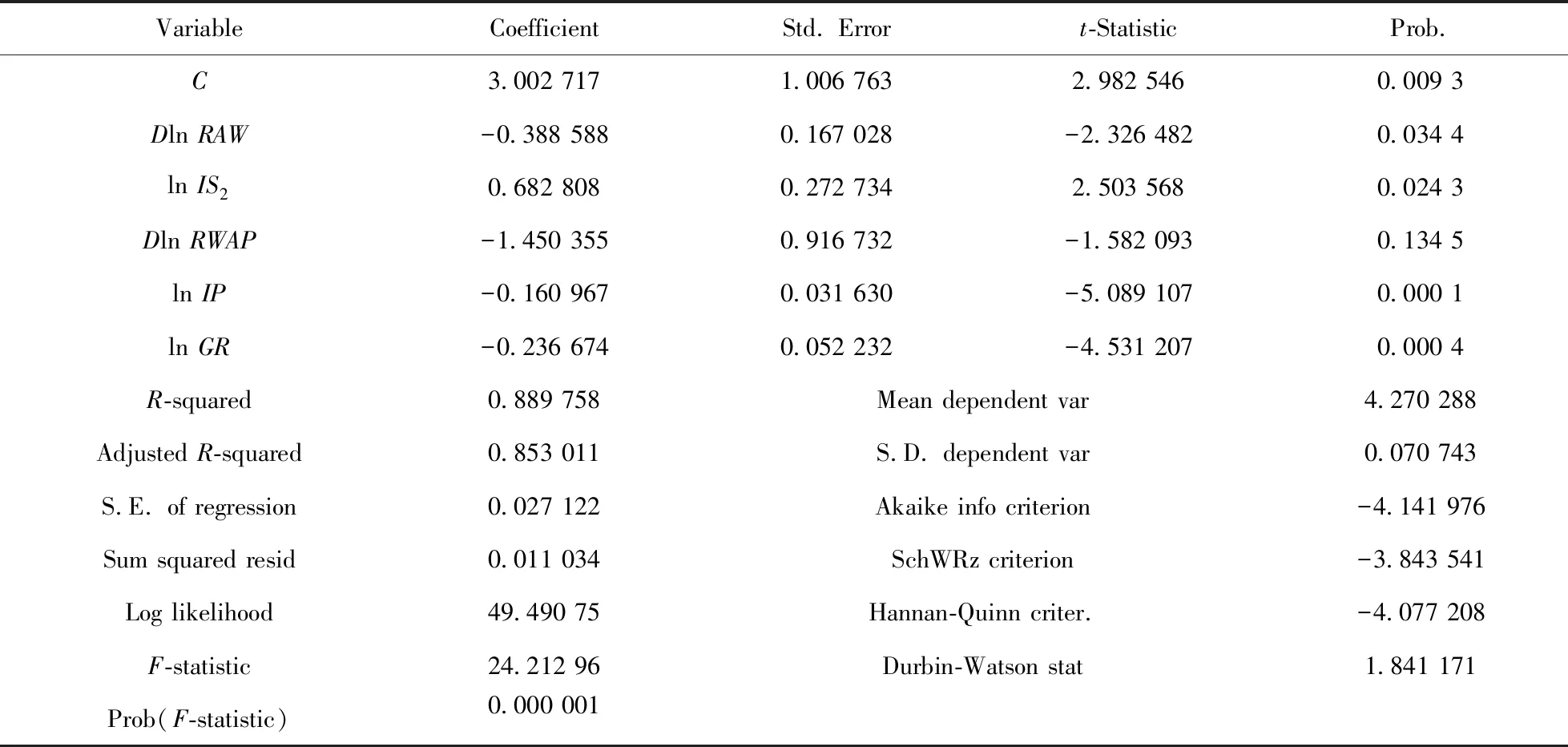
表7 OLS 回歸結果Tab.7 OLS regression results
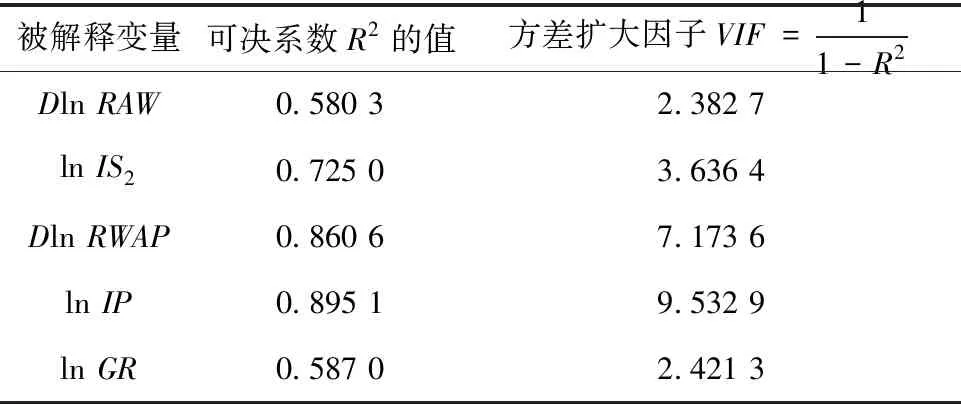
表8 方差擴大因子法檢驗結果Tab.8 Test results of the expanded variance factor method
lnIP的方差擴大因子與10極其接近,表明上述變量存在相當程度的多重共線性.這里采用逐步回歸法補救變量的多重共線性.在經過一元回歸、二元回歸、三元回歸、四元回歸后,最終滿足要求并被保留的解釋變量為lnIS2、DlnRAW、lnIP、lnGR.于是,被解釋變量lnLU回歸模型的估計和Eviews 9.0軟件的輸出結果如表9所示.
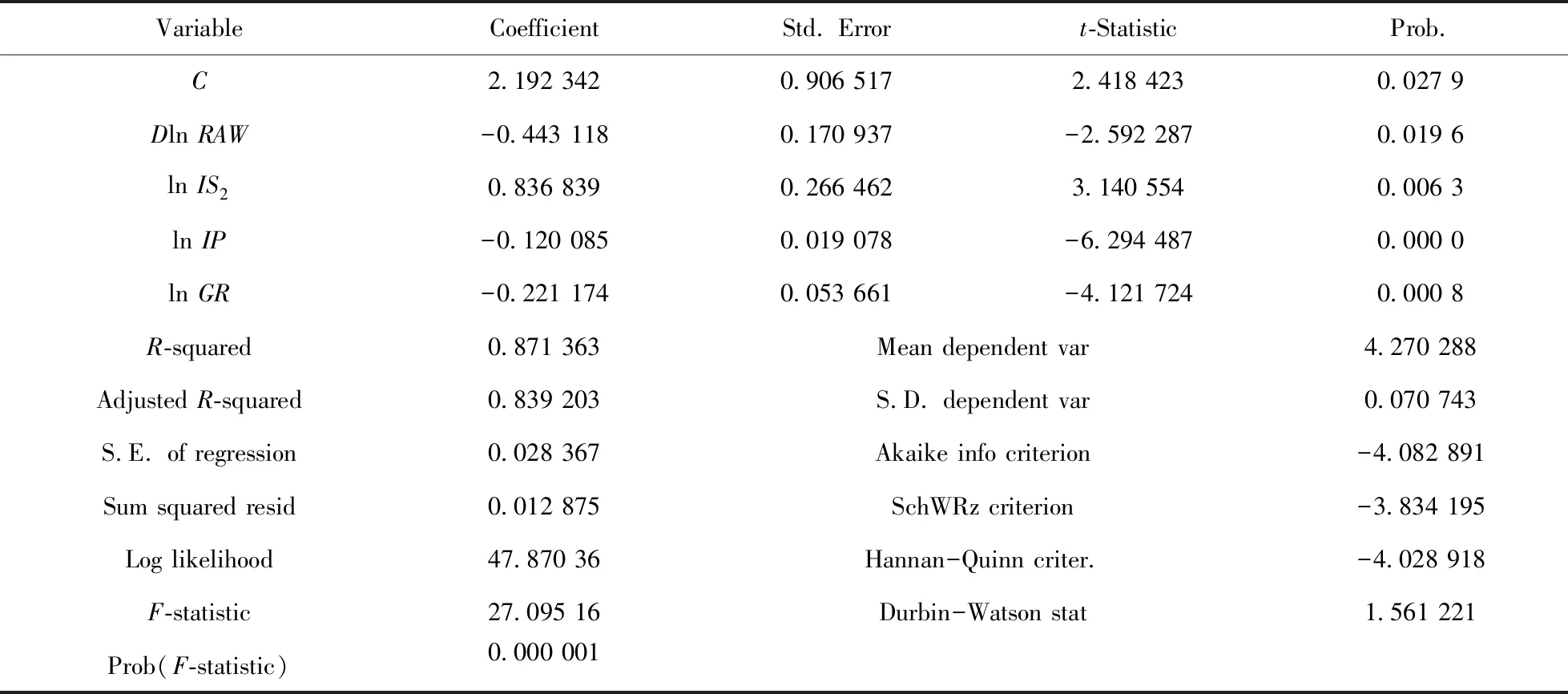
表 9 OLS 輸出結果Tab.9 OLS output results
由于(5)式模型取過一次差分,調整后的樣本個數變為21年,查5%顯著水平的DW統計表可知dL=0.927,dU=0.812,因此有dL lnLU=2.1923-0.4431DlnRAW+ 0.8368lnIS2-0.1201lnIP-0.2212lnGR. (6) (0.9065)(0.1709) (0.2665)(0.0191) (0.0537) t=(2.42)(-2.59)(3.14)(-6.29)(-4.12) F=27.0952,DW=1.561221. 圖2 模型的實際值、擬合值和殘差圖Fig.2 Map of actual value,fitting value and residual (7) (7)式為恒等式,本研究取其作為勞動適齡人口率WR的分析模型. 根據第2章、第3章的分析,可得以下四個模型,以此理清人力資源對人均GDP的作用機理. 人均GDP=勞動生產率(LP)×就業率(LU)×勞動適齡人口率(WR), (8) DlnLP=-14.0027+2.7335lnIS2+ 1.6235lnIS3-0.4788lnID3, (9) lnLU=2.1923-0.4431DlnRAW+ 0.8368lnIS2-0.1201lnIP-0.2212lnGR, (10) WR=戶籍勞動適齡人口率+ 外來勞動適齡人口率. (11) (8)式揭示了人均GDP與勞動生產率、就業率和勞動適齡人口率有直接關系.勞動生產率是通過其水平的變化作用于人力資源需求端,從而影響人力資源需求與供給關系的,勞動適齡人口率是從人力資源供給端直接影響人力資源需求與供給關系的,就業率則是人力資源供需匹配程度的反映.由此可得,人力資源是通過勞動生產率、就業率與勞動適齡人口率三因素作用于人均GDP的. (9)式是對勞動生產率所做的深入解析,它揭示了影響勞動生產率的主要因素及其影響水平與方向.(b)式明顯地反映出地區(武漢市)勞動生產率(DlnLP)第二、第三產業產值比率(lnIS2、lnIS3)關,其中第二產業(Coefficient 2.733478)對勞動生產率的影響遠大于第三產業(Coefficient 1.623496),說明長期以來地區(武漢市25年間)勞動生產率的增長主要依賴第二產業.(b)式還顯示,第三產業密度(lnID3)與生產率(DlnLP)關.由于第三產業是向社會提供服務的產業,而服務主要依賴人的勞動,一個地區第三產業密度的高低決定了其所需人力資源的多少,因而第三產業密度的變化將引起該地區對人力資源需求的變化.總之,第二、第三產業產值比率(lnIS2、lnIS3)三產業密度(lnID3)的均通過引起勞動生產率要素(DlnLP)化最終在人均GDP上得到反映. (10)式是對就業率進行的深入解析.(武漢市)就業率(lnLU)與第二產業產值比率(lnIS2)正相關,與城鎮非私營單位年均工資增長率(DlnRAW)、常住外來人口(lnIP)和地區生產總值的增長率(lnGR)相關,也即對就業率有影響的四個因素中只有第二產業產值比率一個因素對其有正向作用,說明(武漢市25年間)就業率嚴重依賴第二產業.而城鎮非私營單位年均工資、外來人口以及地區生產總值的過快增長都會降低地區(武漢市)就業率,其中城鎮非私營單位年均工資增長率(Coefficient -0.4431)對就業率的負影響遠遠大于另兩者.城鎮非私營單位年均工資是地區人力資源價格的重要標量,有很強的示范作用.人力資源價格(工資)的增長會導致各行業對人力資源需求的較少,從而降低地區就業率. (11)式是對勞動適齡人口率做進一步的解析,說明戶籍勞動適齡人口與外來勞動適齡人口共同構成了一個區域的人力資源供給.顯然,戶籍勞動適齡人口與外來勞動適齡人口同時增長對人均GDP的正向影響作用大,但就目前各地區情況看,兩者同時增長的情況少見.由于受勞動力價格的牽引,發達地區外來勞動適齡人口在增長,欠發達地區增長的戶籍勞動適齡人口部分流向發達地區,因此,增長的人力資源供給推高了發達地區的人均GDP. 綜上分析,本研究得出以下四點主要研究結論. 1) 勞動生產率、就業率和勞動適齡人口率對人均GDP的影響呈乘數效應,三因素中任何一個因素的變化都將引起人均GDP的巨大變化. 2) 勞動生產率是人力資源作用于人均GDP的媒介.勞動生產率與第三產業的產業密度負相關,第三產業密度又影響著其對人力資源的需求,也就是說,人力資源通過第三產業密度的變化引起勞動生產率的變化,最終作用于人均GDP. 3) 就業率是人力資源通過價格作用于人均GDP的結果反映.第二產業的發展對就業率是有明顯的正向作用的,但人力資源價格(工資)的過快增長會兌沖第二產業發展的正向作用,導致就業率的下降,最終引起人均GDP的變化. 4) 勞動適齡人口率是人力資源由供給端作用于人均GDP的要素.在本地區人口增長降低,人力資源供給不足的情況下,只能靠外來人力資源(外來勞動適齡人口)支撐人均GDP的增長. 由于本研究依賴武漢市25年的統計數據,因此本研究對武漢市及與武漢市規模相當產業結構相似的城市更有實踐意義.由此,本研究形成以下兩點結論. 1) 類似于武漢市,如果一個地區第二產業產值率對勞動生產率貢獻較大(如(b)式提示),而就業率又主要依賴第二產業(如(c)式提示),勢必導致地區人力資源向第二產業過度供給,勢必抑制其它產業對人力資源的需求而影響其它產業發展,其結果可能導致地區產業類型轉化及提升變得困難. 2) (10)式提示,類似武漢市這樣的國有經濟成分占比重的城市,要想提高地區就業率必須放慢城鎮非私營單位年均工資的增長速度;同時就業率的增長還要求放慢地區經濟增長速度以調整產業結構.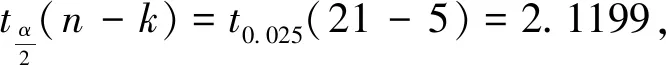
2.3 勞動適齡人口率WR模型

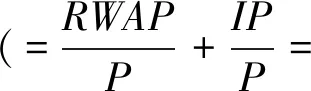
3 分析及結論
3.1 模型分析
3.2 主要研究結論
3.3 其它研究結論

