高考數學考點分析
2020-06-22 01:33:56寧夏
高中數理化 2020年4期
◇ 寧夏 苗 陽
近幾年來,高考數學試題重視對學生數學核心素養的考查,同時兼顧對高中數學主干知識點、學生能力與思想等方面的考查.基礎知識的考查貼近生活、突出重點,重視學生對數學基礎知識在實際生活中的應用意識和學生的數學創新思想,重視培養學生數學核心素養,使學生思維能力水平與數學應用水平得以提高.
1 統計

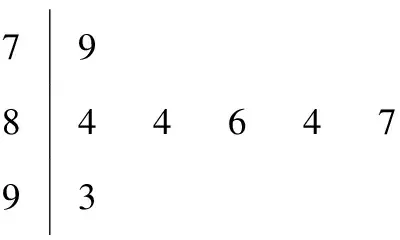
7984464793
圖1
A. 84,4.84 B. 84,1.6
C. 85,1.6 D. 85,4

去掉最低分79與最高分93,平均分為
方差為
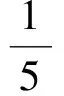
故選C.

2 函數


易知函數f(x)的周期為2π,所以可充分考慮f(x)=2sinx+sin 2x在[0,2π)中的值域.先求函數f(x)在[0,2π)中的極值點.對f(x)求導,得
f′(x)=2cosx+2cos 2x=2(2cos2x+cosx-1)=
2(cosx+1)(2cosx-1),
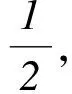
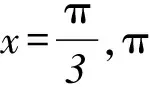

3 遞推數列

(1)求數列{an},{bn}的通項公式;
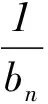

所以,an=2n-1.
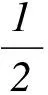
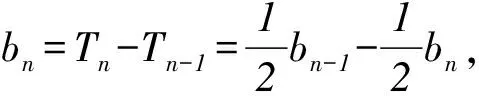
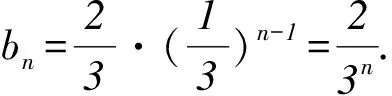
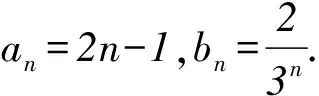
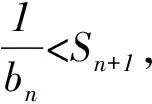

總而言之,高考數學的重點就是對學生的綜合素質進行考查,試題質樸無華,和新課標教學內容貼合,重點為知識應用型與探究性內容,對學生數學創新能力與思維能力要求較高.在備考過程中,要求學生能夠掌握并且理解數學主干知識,使數學思想方法訓練得到加強,并且積極主動地進行數學探究,使學習效率得到提高,從而取得良好成績.
猜你喜歡
趣味(語文)(2021年10期)2021-12-28 09:34:35
師道·教研(2021年2期)2021-03-28 02:20:53
趣味(作文與閱讀)(2021年10期)2021-03-08 09:22:00
意林(兒童繪本)(2020年2期)2021-01-07 02:12:06
新世紀智能(高一語文)(2020年10期)2021-01-04 00:44:12
新世紀智能(高一語文)(2020年10期)2021-01-04 00:44:10
新世紀智能(高一語文)(2020年12期)2020-06-01 08:14:28
新世紀智能(高一語文)(2020年12期)2020-06-01 08:14:26
意林(兒童繪本)(2019年10期)2019-12-23 09:03:36
兒童繪本(2018年19期)2018-10-31 21:02:34

