星座備份策略研究進展

王許煜，胡敏，趙玉龍，徐家輝

航天工程大學，北京 101400

近年來，隨著衛星技術的快速發展，各國對導航和通信等領域的需求也日益增長。然而，為了實現在全球或特定區域內提供連續、穩定的服務，僅依靠單顆衛星遠遠無法滿足，這就需要利用多顆衛星協同工作，以完成任務。衛星星座由多顆衛星組成，各衛星之間通過協同控制在空間中保持相對穩定的幾何構型，并利用多方位的信息互聯，從而實現對目標區域連續的多重覆蓋和性能保證。星座由于其巨大的發展潛力，尤其是在軍事應用中無可比擬的優勢，受到了各國越來越廣泛的關注，呈現迅猛發展的態勢。

作為一個復雜的空間系統，星座的運行管理面臨許多挑戰。星座衛星在軌運行過程中，為了消除攝動力對衛星運行軌道的影響，需要對衛星進行軌道機動以保持其軌道。此外，由于受到衛星自身壽命和可靠性的限制，以及復雜惡劣的太空環境的影響，衛星會出現短期故障(可恢復的故障)或長期故障(不可恢復的故障)[1]。所以，為了保證星座系統一直處于連續且穩定的運行狀態，需要根據其實際狀況采取不同的備份策略。星座備份策略的選取會對星座系統的可用性、連續性和完好性產生直接影響，是星座系統設計的一項重要內容。當衛星發射或運行發生故障時，星座備份是確保星座系統成功組網和穩定運行的關鍵因素[2]。

在星座備份策略研究中，替換策略的優化至關重要。當前，有關替換策略優化的研究主要集中在系統部組件層次，文獻[3]開創性地引入多個單一單元模型，為后續替換策略優化研究奠定了基礎。文獻[4-6]綜述了20世紀50年代初～80年代末有關替換策略優化和模型的發展與應用情況。文獻[7]在此基礎上對該問題進行進一步的總結，認為對于研究相對較少的多單元模型，狀態空間維數問題可能是限制其發展的原因。而由于星座系統的復雜性，關于星座建模及其備份策略的研究則相對較少。

本文歸納總結了3種不同的星座備份策略模式(即在軌備份、停泊軌道備份及地面備份)及其特點。然后，梳理了國內外星座備份策略關鍵因素的研究進展。接著，對目前星座備份策略分析的主要模型和方法進行綜述。最后，展望了星座備份策略研究的發展方向。

1 全球主要星座備份現狀分析

1.1 導航星座備份現狀分析

備份與替換策略一直是GPS星座研究的重要課題。GPS星座最初的設計是由24顆衛星組成，但為了滿足星座中有24顆衛星可以投入運行的概率達到95%[8]，自1993年滿星座運行以來，實際的運行衛星數量一直保持在27顆以上[2,9-10]。GPS星座采取的在軌備份策略是在星座中具有較高故障率的衛星附近部署一顆備份衛星，從而形成一對衛星協同工作，一旦工作衛星出現故障，備份衛星可以經過一次或兩次的軌道機動完成對故障衛星的快速更換[11]。同時GPS還采取了地面備份的策略[12]，在地面上始終有大量等待替換的備份衛星，構成多重備份。

總體來看，GPS在星座組網和運行階段均考慮了星座備份以確保發射和運行穩定，由于大部分衛星均超期服役，使GPS在星座維持上具有相當大的靈活性，并在一定程度上節省了經費。目前GPS系統在軌衛星32顆，其中31顆衛星處于運行階段，1顆衛星處于維修階段。GPS星座空間構型如圖1所示。

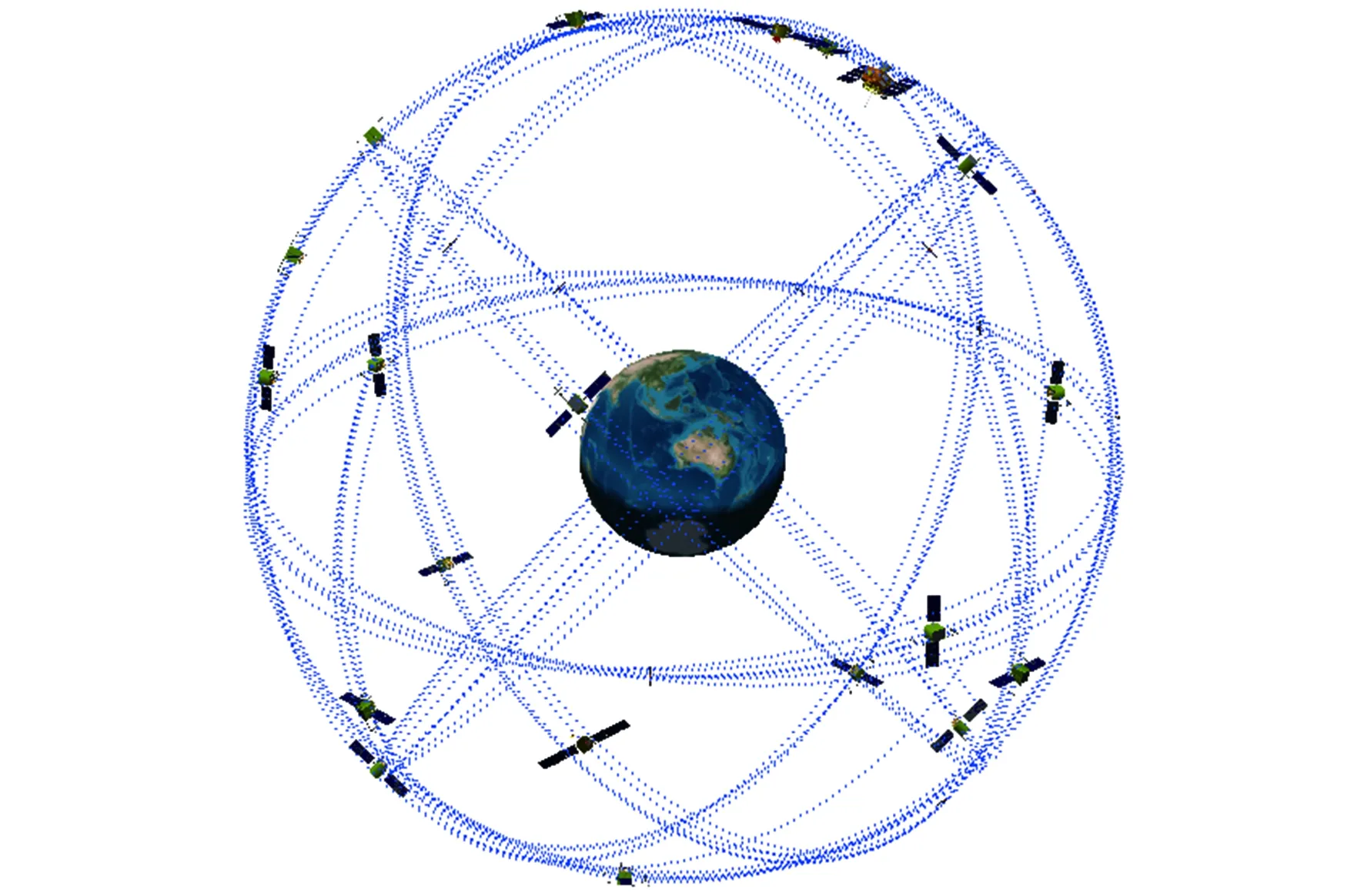
圖1 GPS星座空間構型Fig.1 GPS constellation space configuration

與GPS星座相比，俄羅斯GLONASS星座由于衛星可靠性差，壽命短，導致星座備份維持成本極為高昂。目前GLONASS星座在軌27顆衛星，其中22顆衛星處于正常工作狀態，2顆處于維修狀態，1顆處于飛行測試階段，同時還有2顆在軌備份衛星。GLONASS星座的備份衛星位于同一個軌道面上，且都停止播發導航信號，處于冷備份狀態。當星座中的工作衛星發生故障時，才啟動備份衛星[2]。

表1給出了GLONASS星座備份情況，其中備份衛星COSMOS 2424和COSMOS 2436與其軌道面中最近的在軌運行衛星COSMOS 2522和COSMOS 2534的相位差分別為2.864°和5.842°。

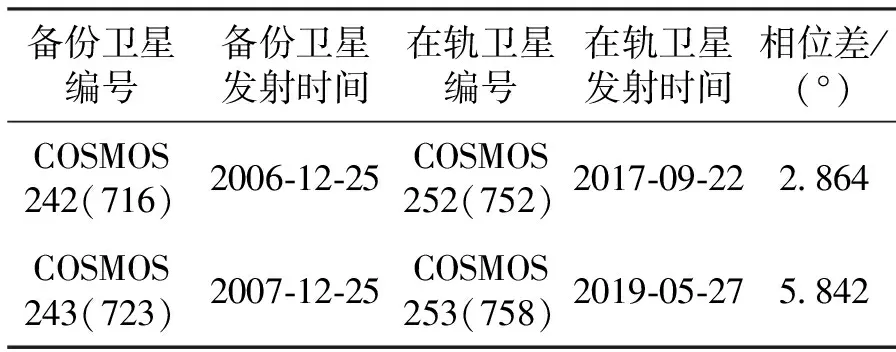
表1 GLONASS星座備份情況

Galileo星座在考慮星座備份時借鑒了GPS的經驗，在設計階段詳細研究了星座組網與可靠運行問題。Galileo星座采用3個傾角為56°的軌道面組成的Walker星座，由27顆運行衛星組成，采取在每個軌道面上部署一顆備份衛星的策略。與GLONASS星座一樣，Galileo星座的備份衛星也處于冷備份狀態，當工作衛星發生故障時，備份衛星通過移動來更換故障衛星，從而快速修復星座中的故障，而不需要等待安排新的衛星發射[13]。

綜上分析，現有導航星座GPS、GLONASS以及Galileo采取的星座備份策略如表2所示。

表2 導航星座備份策略

1.2 通信星座備份現狀分析

在商業通信星座中，通過按需發射來替換故障衛星，這可能會導致無法接受的延遲[14]，所以通信星座一般采用在軌備份或停泊軌道備份和地面備份相結合的模式。

第一代Iridium星座由6個傾角為86.4°的軌道面組成，每個軌道面上部署11個工作衛星以及1個備份衛星，其中工作衛星軌道高度為780 km，備份衛星軌道高度為648 km，略低于工作衛星軌道高度[15]。由于第一代Iridium星座的老化和升級，2019年1月銥星公司與SpaceX完成了第二代Iridium星座75顆衛星的部署，包括66顆在軌工作衛星和9顆備份衛星，同時還有6顆地面備份衛星。

GlobalStar第一代星座由48顆工作衛星和8顆備份衛星組成，工作衛星均勻部署在8個傾角為52°，高度為1 414 km的圓形軌道上，同時在每個軌道面部署1顆備份衛星，備份衛星的軌道高度為900 km，低于星座的運行軌道[16]。Globalstar星座自2016年2月全面部署以來，目前共有32顆運行衛星，包括8顆第一代衛星和24顆第二代新衛星，旨在提高星座的覆蓋范圍和可靠性[17]。

為了提供寬帶服務，OneWeb計劃生產900顆衛星，在低地球軌道(LEO)建立一個大型衛星星座，星座共有648顆衛星部署在18個高度為1 200 km，傾角為87.9°的軌道平面上，其中有600顆工作衛星以及48顆在軌備份衛星，其余衛星將用作地面備份。

SpaceX正在規劃一個由近1.2萬顆相互連接的寬帶互聯網衛星組成的巨型星座(Starlink)，該星座具有兩個子星座。第一個子星座由4 425顆衛星(包括備份星)組成，衛星分布在83個不同高度和不同傾角的軌道面上，軌道高度1 110～1 325 km，軌道傾角53°～81°，同時計劃在每個軌道面部署兩顆備份星，以便在衛星故障時補充星座。如果工作衛星沒有發生故障，則備份星將處于休眠狀態，即冷備份，并將與其他活動衛星一起保持星座構型以及規避碎片碰撞的操作。第二個子星座共有7 518顆衛星，部署在3個不同高度和不同傾角的軌道面上，軌道高度分別為345.6 km、340.8 km和335.9 km，軌道傾角分別為53°、48°和42°[18]。

2 星座備份策略模式

備份策略是指為了防止因工作衛星發生故障而導致星座無法滿足所需性能要求時，采取的星座冗余配置設計[19]。為了提供長期服務，星座必須考慮到更換個別衛星的需要[20]。備份策略通常包括3種模式：在軌備份、停泊軌道備份以及地面備份，前面兩種統稱為空間備份[11]。由于空間備份模式具有平均修復時間較小的優勢, 在星座系統備份中得到了廣泛的應用[21]。

2.1 在軌備份模式分析

在軌備份模式是將備份衛星部署在與星座標稱軌道相同的高度上，每個軌道面一般需要放置至少一顆備份衛星，但是這種備份方法需要較多的衛星，具有較高的成本。當星座中的工作衛星發生故障時，備份衛星將通過相位調整，分階段到達所需的位置，從而對故障衛星進行快速替換，只要合理使用燃料，故障衛星在幾天內就可以完成更換。在軌備份模式由于具有快速替換故障衛星的優點，所以是星座備份中最常用的一種模式。

在軌備份的另一種形式是激活備份衛星并將其作為星座的一部分使用[22]，以達到冗余備份的目的，從而有效增強星座的服務性能，使其處于最佳運行狀態，同時提高星座的魯棒性，減少故障快速替換的需求[23]。然而，冗余備份模式一旦發生故障，星座內的許多衛星可能不得不通過重新發射新衛星的方式來替換。冗余備份模式通常包括以下兩種方式：

1)單星備份。在達到服務性能要求的星座標稱構型上，給每個軌道面額外部署一顆備份星。倘若星座中的工作衛星出現故障無法提供服務，由于備份衛星處于工作狀態，所以不需要調整備份衛星的軌道相位就可以滿足服務性能的最低要求，同時也給予備份衛星充分的重構時間。

2)雙星備份。對于具有非常高可用性需求(99.9%甚至更高)的星座，采取在每個軌道面上部署兩顆備份衛星的雙星備份將會是一種更好的選擇[24]，這不僅可以提高星座備份的效率，縮短備份時間，同時在服務性能增強方面也具有積極的作用[25]。除非衛星遭受打擊，否則在同一軌道面上很難出現3顆或更多的衛星同時發生故障的情況[26]，所以，通常不考慮備份3顆衛星的方式。

2.2 停泊軌道備份模式分析

停泊軌道備份是將備份衛星部署在低于星座軌道高度的停泊軌道上。由于軌道高度差的存在以及攝動力引起的相對相位角變化，停泊軌道面會相對星座軌道面不斷漂移，在停泊軌道漂移的過程中，備份衛星可以根據實際情況對不同的軌道面進行故障衛星替換，所以一般會在停泊軌道上部署多顆備份衛星。當備份衛星軌道面調整至與星座軌道面重合時，備份衛星通過提升軌道高度，然后進行相位調整，分階段到達星座軌道上所需的位置，這樣可以消耗較少的燃料。然而，停泊軌道備份模式利用軌道漂移來調整備份星軌道面需要較長時間，特別是對于在近地軌道(LEO)的應用，如果軌道高度差異很小，則相對相位角變化速率也很小。所以，采用這種備份模式替換一顆故障衛星的時間通常約為1～2個月[22]。

文獻[24]從軌道高度和軌道傾角兩個方面討論了備份衛星停泊軌道的設計，綜合考慮了衛星控制速度、故障衛星平均修復時間以及備份星數目等因素，得到停泊軌道模型。通過分析，筆者認為在一定的軌道傾角容許漂移量內，備份衛星只需要在備份軌道內通過相位調整即可實現快速替換故障衛星，但與此同時也要綜合考慮調整軌道面的一致性所消耗的燃料。

相較于在軌備份模式，由于衛星替換時間較長，停泊軌道備份的備份效率較低。同時，部署在停泊軌道上的備份衛星一般都處于冷備份狀態，所以該備份模式達不到增強星座性能的效果。綜合上述原因，對于可靠性和可用性要求非常高的導航星座來說，這種備份模式并不適用。然而，如果星座對可用性的要求小于95%，則可以首先選擇停泊軌道備份模式[27]，如Iridium星座、GlobalStar星座等通信星座一般都會采用停泊軌道備份模式。

星座采用停泊軌道備份模式需要綜合考慮以下因素[28]：備份衛星通過軌道機動從停泊軌道轉移到星座軌道所需的ΔV，備份衛星在星座軌道內調整相位并重新定位所需的ΔV以及衛星故障與星座服務性能恢復之間的時間延遲。

2.3 地面備份模式分析

地面備份模式是將備份衛星存儲在地面上，如果星座中的工作衛星發生故障，則立即發射備份衛星以替換失效衛星。這種模式的好處是備用衛星可用于測試和改進，直至發射時為止，同時只需在地面存放少量的備份星即可達到備份的目的。然而，由于這種備份方式發射周期長，所以需要很長的時間才能實現對故障衛星的替換，一般都需要數月或者一年甚至更長的時間[29]。地面備份方式可能因為備份星發射延遲而導致星座長時間服務中斷，所以這種備份模式一般只適用于對可靠性和可用性要求不高的星座。

2.4 星座備份策略模式比較

從維持星座性能的角度看，最佳的備份模式始終是在軌備份，然而，根據星座的性能要求，在軌備份可能需要備份多顆衛星以提供更高的服務性能。特別是對于具有多個軌道面的星座，若每個軌道面至少部署一顆備份星，則需要制造和發射許多額外的衛星，導致較高的備份成本。

在停泊軌道備份模式中，一顆備份星可以對不同軌道面進行備份，如果有較多的停泊軌道，盡管軌道漂移速度慢，但仍然可以在一定程度上縮短替換故障衛星的時間。然而隨著停泊軌道的增多，需要制造和發射更多的備份星，同樣會提高成本。

當星座對服務性能要求不高時，則可以采用地面備份模式。由于所需備份衛星較少，從長遠來看，相比于其他兩種備份，地面備份具有最低的備份成本。但該模式替換故障衛星所需的時間最多。所以這種模式通常作為前兩種模式的后備模式，與前兩種模式結合使用。表3給出了3種備份模式的對比。

表3 星座備份策略模式對比

3 星座備份策略的關鍵因素

星座備份策略的研究受到許多因素的影響，包括星座運行中的各種確定性因素和隨機因素。針對現階段星座備份策略的主要模式與星座服務性能需求，本節重點論述星座備份策略中衛星故障模式、衛星可靠性、衛星可用性、星座狀態概率和星座系統可用性等5項關鍵因素。

3.1 衛星故障模式分析

在星座運行的過程中，由于受到空間環境和自身組件損耗的影響，星座中的衛星會發生故障，從而改變星座的運行狀態，影響星座的服務性能。因此必須確定星座的運行管理計劃，降低星座壽命周期內衛星故障的影響，以避免嚴重的服務中斷[30]。衛星故障可以分為以下幾種類型[31]：

1)長期故障：衛星中的單個或多個組件發生故障，且不可通過在軌維修或使用星載備份進行修復，從而導致衛星不再正常工作。一旦發生長期故障，若不及時使用備份衛星，會對星座的服務性能造成極大的影響。

2)短期故障：衛星發生故障后會暫時停止工作，通過及時的在軌維修或者使用備份組件對故障組件進行替換，可以在幾小時或幾天內恢復功能。短期故障由于其可恢復性，對星座的服務性能影響是有限的，所以并不需要使用在軌備份星或發射新衛星進行替換。

3)維護故障：為了保持星座空間構型或提高衛星性能，會對星座進行維護操作，在此期間所導致的衛星停止提供服務，雖然也會降低星座的服務性能，但通常不認定其為“故障”。由于星座一般都具有預先制定的維護計劃，所以并不會因此導致服務的中斷，仍然具有連續性。

為了更好地描述衛星運行期間的各類故障，一般都使用以下參數[25]：

1)平均故障間隔時間(Mean Time Between Failure，MTBF)：對于長期故障，由于衛星發生故障即永久失效，該參數一般指衛星實際運行壽命的平均值；而對于短期故障，該參數一般用來度量衛星相鄰故障之間的時間間隔的平均值。

2)平均維護間隔時間(Mean Time Between Maintenance，MTBM)：指星座進行維護操作的平均時間間隔。

3)平均修復時間(Mean Time To Replace，MTTR)：對于長期故障，該參數是指備份衛星替換故障衛星并進行正常工作所需要的平均時間；而對于短期故障和維護故障，一般是指修復短期故障以及維護操作所需的平均時間。

3.2 衛星可靠性建模分析

可靠性的定義為在特定的條件和時間下，產品能完成指定任務的能力[32]。衛星系統可靠度一般根據設備或分系統可靠性預計值利用系統可靠性模型計算得到[33]。衛星可靠性的提高，不僅可以保證維持星座正常布局和運行的可用衛星數量，而且可以降低衛星的中斷頻率，從而減少備份衛星發射的次數和成本[34]。但是，僅僅依靠增加單顆衛星的可靠性來滿足所需的星座可用性, 將需要采用大量的冗余度設計，包括增加衛星零部件備份或者在星座系統中部署更多的備份星，會直接導致衛星研發、制造以及發射費用的增加[35]。

傳統的衛星可靠性模型一般都采用指數模型，Ochieng 等[36]通過假設衛星的故障概率密度函數服從指數分布得到相應的壽命分布，最終得到衛星可靠性指數模型：

R(t)=e-λt

(1)

式中：λ為故障率，其數值為1/MTBF。

文獻[12,37-38]中也都采用了指數模型來描述衛星可靠性，然而傳統的衛星可靠性模型雖然有利于簡化和分析問題，但假設故障率是常數，不能準確地描述衛星早期故障、損耗累積和老化的過程。通常，由于早期故障期，在衛星早期的運行中具有較高的故障率，然后隨著衛星零部件開始損耗，故障率在衛星生命末期會迅速增加[39]。

文獻[40]介紹了用于星座可靠性和可用性分析的軟件(Operational Constellation Availability and Reliability Simulation，OSCARS)，在OSCARS中衛星可靠性模型可以通過單個概率分布或者通過不同的概率分布來表示衛星各個壽命階段(早期故障期、工作壽命期和損耗期)來建立。早期故障期可利用用戶指定的概率分布進行建模。利用Weibull分布可以建立衛星工作壽命期可靠性模型，同時該文獻指出，Weibull分布經常被用于模擬衛星故障。損耗期有4種不同的建模方法，第一種方法被描述為一個固定的截止日期，即衛星故障要么發生在指定日期之前，要么發生在指定日期，其他方法包括瑞利分布、正態分布和具有固定截止日期的正態分布。

文獻[41]通過研究衛星子系統對衛星可靠性進行分析建模，通過將一個指數分布和一個有3個參數的Weibull分布進行線性組合，提出了一個具有5個參數的故障概率密度函數，其中指數分布用來模擬一個組件的初期故障期，Weibull分布用來模擬組件的剩余壽命。該文獻指出，利用這個概率密度函數進行可靠性建模考慮了組件的實際情況，可以替代組件壽命的指數模型。組件的故障概率密度函數可以寫為：

f(x)=PIMfIM(x)+(1-PIM)fW(x)

(2)

其中：

式中：fIM(x)表示指數分布；fW(x)表示Weibull分布；PIM為早期故障概率；θIM為早期故障期的預期壽命；δ為最短壽命期；θ為比例參數；β為形狀參數。

文獻[42]借鑒了GPS星座的經驗，考慮了隨機故障和損耗故障，建立了更為準確的衛星可靠性模型：

(3)

式中：α為尺度參數；μ為均值；σ為標準差；t為衛星的使用時間。

文獻[42]分析了衛星在整個壽命周期內的可靠性變化，并與指數模型進行了比較。從圖2中可以看出，與傳統的指數模型相比，改進模型在衛星壽命期內可靠性比較穩定，超出設計壽命后可靠性急劇下降，這與衛星的實際狀態更為符合，更能描述衛星在整個壽命周期內可靠性隨時間變化的真實狀況。

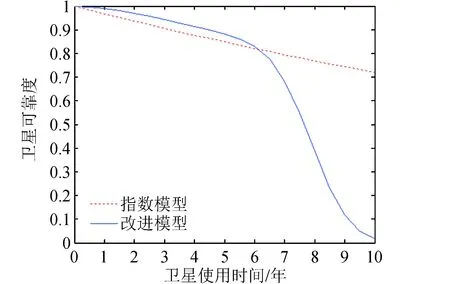
圖2 衛星的兩種可靠性模型對比情況Fig.2 Comparison of two reliability models of satellites

衛星可靠性模型的準確性關系到衛星末期可靠性和衛星剩余壽命的預測，從而影響星座備份策略的最終選取。表4給出了4種衛星可靠性建模方法的對比。

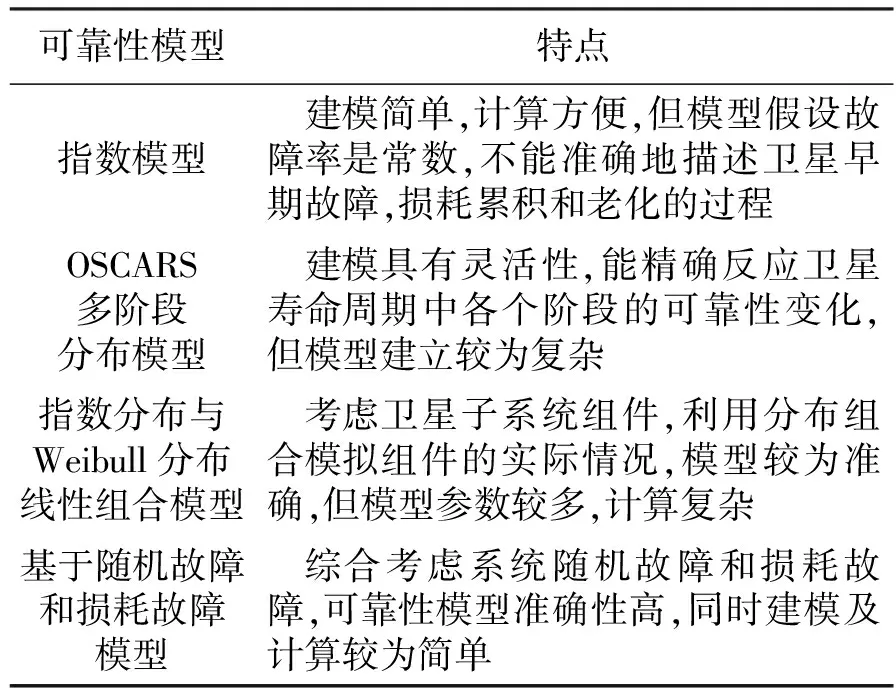
表4 衛星可靠性建模方法比較

3.3 衛星可用性研究分析

可靠性研究只考慮了單個衛星的故障率，并沒有綜合考慮衛星在軌修復或按需替換的特性，而可用性則用于表示衛星處于工作狀態的程度，是衛星可靠性和可維護性的綜合反映。衛星不同的故障模式所導致的服務中斷是影響衛星可用性的一個直接因素。

文獻[43]首先給出了單顆衛星可用性的計算方法，并在此基礎上分析了衛星處于長期故障和短期故障模式下的衛星故障率。由于長期故障和短期故障的不同特性，作者討論了短期故障下的衛星修復率，并綜合考慮星座在軌備份和地面備份策略，給出了長期故障下的衛星修復率，最終得到等效的衛星故障率λ和衛星修復率μ。

文獻[25]同樣基于衛星不同的故障模式以及星座備份策略，利用馬爾可夫狀態轉移模型對單顆衛星進行了分析，最終得到衛星的穩態可用性。然而與文獻[43]不同的是，作者還考慮了維護操作所引起的故障對衛星可用性的影響。同時文章還利用文獻數據進行了實驗分析。實驗結果表明，當平均故障間隔時間增加，處于長期故障模式下的衛星可用性提高最為顯著。通過對3種故障模式進行比較，可以得出衛星可用性最容易受長期故障模式的影響，而受維護故障模式的影響則最小。所以提高衛星處于長期故障模式下的平均故障間隔時間，對可用性的提高有著十分積極的作用。

文獻[19]針對衛星星載組件壽命周期和故障恢復時間服從以及不嚴格服從指數分布的情況，分別對衛星可用性進行建模分析。對于服從指數分布的情況，作者利用連續時間馬爾可夫鏈(Continuous Time Markov Chain，CTMC)模型，并基于 Laplace變換給出該模型的求解方法，從而得到衛星的瞬時可用性，進一步得到單顆衛星的穩態可用性。衛星可用性表示為:

(4)

式中：MTBF=1/λ；MTTR=1/μ。

而對于不嚴格服從指數分布的情況，則利用時齊半馬爾可夫過程(Semi-Markov Process，SMP)模型。模型中使用統計抽樣的方法對狀態轉移概率進行了估計，同時還進一步估算了轉移參數并獲得狀態的分布矩陣，最終計算得到單顆衛星的瞬時可用性。

3.4 星座狀態概率計算分析

文獻[42]定義了在不同時刻下星座的所有可能狀態，并根據衛星的可靠性計算出不同狀態下的星座狀態概率。由于各衛星的可靠性不同，所以不同故障衛星組合下的星座狀態概率也不同，可得：

(5)

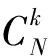
文獻[42]雖然利用衛星的可靠性計算出了星座不同故障狀態下的概率，但忽略了星座備份策略的影響。文獻[25]則在不同衛星故障模式的基礎上，采用時齊馬爾可夫鏈模型，充分考慮了星座備份策略，通過假定星座系統的衛星故障率、修復率及狀態轉移時間間隔得到相應的狀態轉移矩陣，然后根據星座狀態的初始條件求得在相應時間間隔后星座處于不同狀態的概率。馬爾可夫鏈是一種常用的星座狀態概率估計工具，在文獻[44-45]中，作者同樣都采用了馬爾可夫鏈對星座狀態概率進行建模分析。

3.5 星座系統可用性模型分析

星座系統通常選擇服務可用性作為其性能指標，主要指衛星提供的服務在目標區域內能滿足用戶需求的時間百分比[43]。星座系統可用性在實際應用中具有非常高的價值，通常是星座構型設計、分階段部署和備份策略選擇的主導因素之一[46]，其數值一般取決于星座狀態和星座的幾何構型。隨著星座運行時間的推移，衛星可靠性會隨之發生改變，一些衛星可能會因故障而停止工作，因此星座狀態概率也在發生動態變化。與此同時，星座中故障衛星的出現會導致星座的幾何構型發生改變，從而影響星座性能。因此，星座的可用性會隨著運行時間的變化而變化[42]。可用性的優化是一項極其復雜的系統工程，需要投入足夠的精力來做出決策[34]。

在一定的平均修復時間內，星座所達到的性能水平可以很好地反映整個星座生命周期內的可用性[47]。星座的服務可用性可以定義為星座狀態概率和星座值相乘之和。在文獻[40,48-49]中利用此定義給出了星座系統可用性模型：

(6)

式中：N為衛星數目；CVk(t)為t時刻下有k顆衛星故障時的星座值，反映星座的幾何特征和連續可見性，是星座性能的重要表現。

在其他文獻中，文獻[34]研究分析了單顆衛星可靠性與星座可用性之間的關系，并利用蒙特卡洛方法對星座可用性進行模擬仿真。文獻[50]基于馬爾可夫過程給出了單顆衛星可用性算法，并利用星座狀態概率對星座可用性進行了建模分析。

4 星座備份策略模型與方法研究

對星座進行備份能有效避免星座因衛星故障而發生嚴重的服務中斷。在星座備份策略研究中，采用不同的模型與方法將直接影響星座備份策略的選取與優化，針對各模型與方法的特點及其適用解決的問題，本節重點綜述目前星座備份策略分析的主要模型和方法，包括Petri網、馬爾可夫鏈以及存儲論。

4.1 Petri網模型和方法

文獻[2]利用Petri網建立了具有多約束的星座運行狀態變化模型，將星座在不同時刻所發生的事件當作Petri網模型的變遷，通過變遷來實現星座狀態的動態變化。模型綜合分析了星座運行過程中的確定性因素(如星座備份策略、星座運行邏輯)和不確定因素(如衛星故障時間、故障恢復時間)，并依據各事件發生的概率模擬仿真了星座系統的實際運行情況。最后作者利用蒙特卡洛方法分析了在不同備份策略下星座系統可用性的隨機分布情況。

Ereau等[51]利用Petri網討論了星座可用性問題。通過Petri網對星座進行建模，該模型通過一個由不同模型段的較小Petri網所組成的全局Petri網來實現。作者指出，與其他類型的模型相比，使用Petri網對衛星星座進行建模能夠更好地處理星座狀態數的組合爆炸，并且可以在不改變模型的情況下對輸入參數進行廣泛的敏感性分析。為了得到模型的定性結果，作者采用了蒙特卡羅仿真，同時指出，由于要用于問題的定量分析，Petri網必須拓展為包含時間的使用，即為隨機賦時Petri網，但是為了合理地利用時間，分析結果仍將面臨狀態空間爆炸的問題。

Petri網作為一種既具有數學分析和仿真的能力，也有直觀的圖形表達能力的建模工具，可以詳細地表達系統中的運行邏輯，反映系統的靜態布局以及動態變化，目前已成為星座模型建立的主要工具之一。但當星座衛星數量增大時，Petri網模型將發生狀態爆炸，從而提高了模型復雜度，導致計算量增大。

4.2 馬爾可夫鏈模型和方法

文獻[6]從分析的角度探討了衛星最優替換策略的確定問題。作者采用離散時間馬爾可夫決策過程進行建模，允許衛星星座在每個決策元處于有限數目的狀態，并利用馬爾可夫決策過程(隨機動態規劃)的標準策略評估算法，對系統在給定時間范圍內進行評估，以確定最優的替換策略和最小的預期總成本。同時，還對模型參數進行敏感性分析，為評估最優值如何受到模型參數變化的影響提供了一種方法。在問題分析的過程中，作者對衛星及其運行進行了若干假設，如沒有發射提前時間和只考慮地面備件，來限制Ereau和Saleman提出的星座狀態爆炸問題，但這些假設是有局限性的。此外，特別是對于大型星座而言，星座狀態數仍然非常多，例如，對于一個由9顆衛星組成的星座，其運行狀態數就達4 680個。

Kelley等[52]也使用馬爾可夫鏈模型來評估星座系統的壽命周期成本，包括衛星的獲取、補給以及運行成本，并在成本和性能兩個主要部分之間建立了適當的聯系。作者還利用全局優化技術(模擬退火和遺傳算法)對局部優化技術(單純形和復形)的性能進行了評估，以提供星座覆蓋的可用性，并通過比較發現遺傳算法的全局優化性能略好于模擬退火算法。但是同樣的，這種模型會隨著星座規模的增大而導致星座狀態爆炸，因此無法拓展到大型星座。

文獻[53]首先給出了單個衛星形式規范及其相關的連續時間馬爾可夫鏈模型，并在此基礎上對星座系統進行建模分析。然后利用概率模型檢查工具PRISM[54]對單個衛星和星座的可靠性、可用性和可維護性(RAM)進行了分析。系統的可靠性、可用性和可維護性分析在衛星的設計階段必不可少，以便實現最小的故障或增加平均故障間隔時間，從而規劃維護策略，優化可靠性和最大限度地提高可用性。

到目前為止，星座模型分析多采用馬爾可夫鏈方法。馬爾可夫鏈建模較為簡單，可以得到系統的穩態特性，具有建模便利和求解快速的優點[2]。但是由于模型建立過程中對實際問題做出了過多的假設，具有局限性。同時與Petri網一樣，隨著星座中衛星數量的增多，會導致星座狀態爆炸和計算效率下降。

4.3 存儲論模型和方法

利用庫存管理方法對衛星星座備份策略進行建模的文獻較少。文獻[55]從簡單的衛星層面分析了衛星的補給問題，并使用經典的(N,M)庫存系統解決了這個問題。模型考慮了星座系統中運行衛星的總數, 當衛星總數從M降到N時，就開始對星座進行補網發射，使系統衛星總數重新到達M。并利用衛星隨時間發射的數量成本函數，推導出一種最優策略。然而，文獻所提出的庫存模型非常簡單，并具有局限性：首先，衛星總數補給到M的過程中不允許一致的發射計劃；其次，它不能反映衛星批量發射可以節省成本的真實性，也沒有明確考慮停泊軌道的使用。這些局限性使得所提出的策略不適用于大型衛星星座。

文獻[56]利用庫存管理的方法，考慮了一組低于星座軌道高度的停泊軌道用于存儲備份衛星，并利用多級(s,Q)庫存策略對星座備份策略進行建模，提出了一種基于停泊軌道特性和所有位置政策的優化備份策略，然后在滿足系統性能要求的前提下，對系統的維護總成本進行了優化設計。該模型將衛星星座備份策略看作一個多層次的備份供應鏈系統，旨在同時考慮系統中不同級別的備份衛星，將地面備份看作供應商，停泊軌道備份看作倉庫，而在軌備份則看作零售商。在此基礎上，模型假設了隨機需求(故障)和備份交付時間，并通過拉丁超立方抽樣仿真，對所提出的分析模型的精度進行了評估。作者強調了衛星通過批量發射來節省成本的重要性以及多個停泊軌道為所有軌道面提供備份所帶來的靈活性，并說明了該多級混合策略對大型星座的價值。多級(s,Q)存儲策略補給周期示意如圖3所示，當庫存中的存儲水平下降到或低于s個可用單元時，將向其供應商發出數量為Q的訂單。

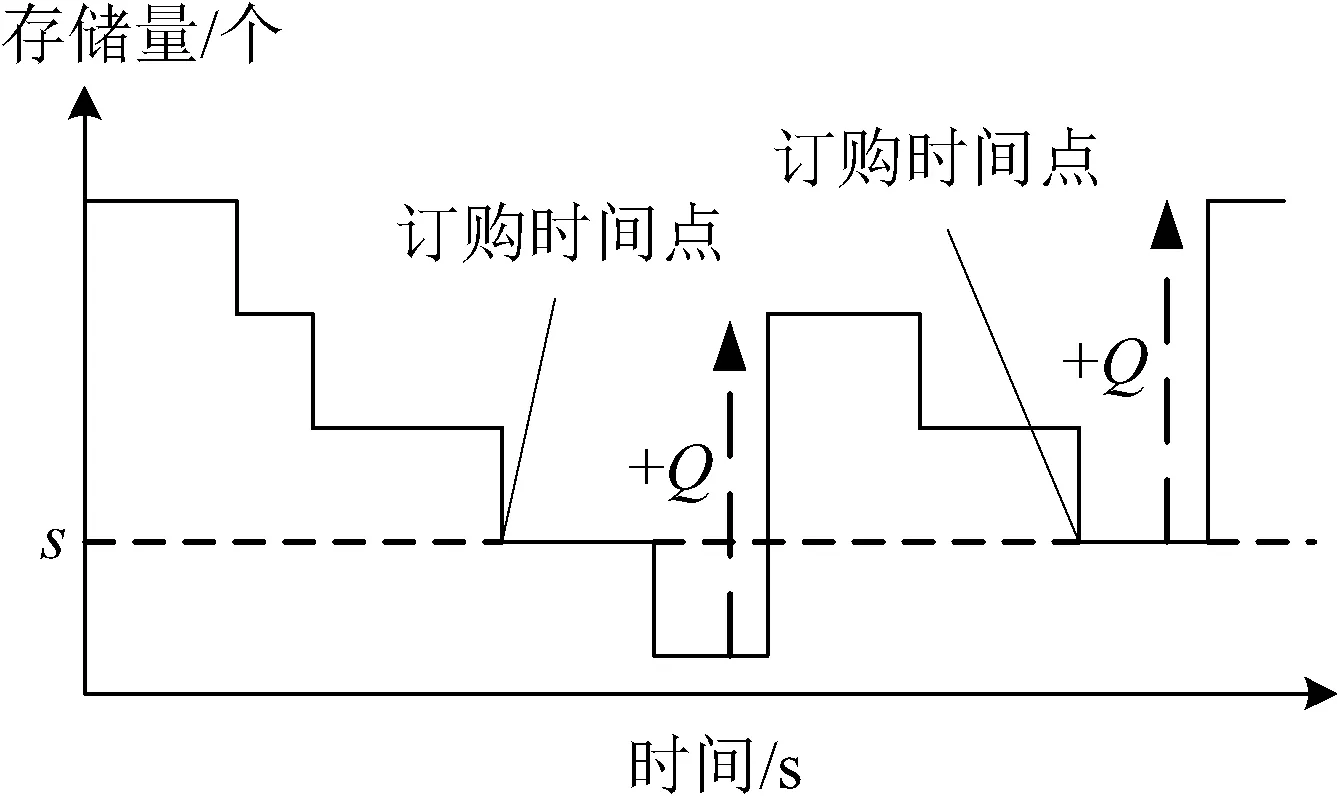
圖3 (s,Q)存儲策略補給周期示意Fig3 Illustration of (s,Q)inventory policy replenishment cycles

利用存儲論對星座備份問題進行建模可以有效解決由于星座衛星數目增大導致的星座狀態爆炸的問題，同時該模型能提高星座備份策略的靈活性，為大型的導航、通信星座的備份問題提供了參考。但由于存儲論綜合考慮了不同星座備份策略的應用，使得星座模型的建立較為復雜。

5 總結和展望

星座備份策略研究涉及多個領域，具有多重的約束條件和性能指標，是極為復雜的工程問題。為了得到理論上最優的備份替換策略，必須對多個因素進行假設分析，這為該問題提供了更多的研究方向。星座備份問題可以在以下方面開展進一步的研究：

1)目前的衛星可靠性模型通常假設服從指數分布或幾個分布的組合。然而，通過對衛星可靠性的分析，可得衛星具有早期故障這一問題。為了更準確地反映實際情況，需要觀測在軌衛星以提供準確的故障數據，從而建立更為真實可靠的模型。

2)星座模型建立的過程中，為了簡化問題假定衛星在軌狀態為可操作或不可操作。然而對于單個衛星來說，當部分組件發生故障時，衛星仍可以處于運行狀態。所以需要利用多個狀態來表示衛星在不同時期的健康狀況從而更準確的描述現實場景，并在退化狀態下對衛星進行評估以確定合理的替換時間點。

3)對地面備份進行更深入的研究分析是模型的另一個拓展。由于在星座的運行過程中，需要在衛星預期故障之前訂購備份衛星，這可能導致星座需要補網時無法及時獲得備份衛星，或者在衛星發生故障之前為存儲地面備份衛星而花費高額的費用，所以需要對替換訂單的提前時間開展深入分析。另一方面，衛星存儲在地面的過程中，衛星技術和設計的進步可以提升衛星的壽命和能力，但若對衛星進行改造將增加成本，所以需要對這種更為現實的因素開展綜合分析。

4)在星座備份策略研究中，最佳替換策略的目標函數通常單一地考慮最低預期總成本、最佳服務性能或幾何覆蓋準則等因素。而如今對單一條件的滿足已無法實現星座對不同任務的要求，必須在最優效率水平上進行權衡，這就需要對包含不同效率結果的代價目標函數開展計算研究。