超級柵板衍射強度角譜的數學探究
2020-06-23 02:20:52王春艷鄔志強王厚增
高師理科學刊 2020年5期
王春艷,鄔志強,王厚增
(齊齊哈爾大學 理學院,黑龍江 齊齊哈爾 161006)
1 引言及預備知識
聲學超表面是聲學超材料的分支,以其靈活的聲波調控特性成為超材料領域的研究熱點[1].聲超表面是由周期性亞波長元素組成的,通過合理設計周期元素的位置,超表面可以實現聲波的多種功能[2].為了控制波跡,超表面必須在不同的位置提供相應的相位剖面.這種相位分布通常是由廣義衍射定律推導出來的,從而導致了對工作頻率的固有依賴[3].因此,奇異相位使得超表面只能在窄帶內工作.作為一種新興的超表面,人工超級光柵由于具有比普通相位光柵更多的組合功能和更優越的性能而備受關注[4].超級柵板衍射強度特性的研究是至關重要的,在理論上主要用角譜方程來研究衍射特性,本文利用數學的方法研究其衍射角譜方程.


2 主要結果及證明
定理衍射強度的角譜為

證明根據規則相位光柵的原理,當平面波垂直入射到柵板時,柵板的衍射角度滿足光柵方程,其中:m(m=0,±1,±2,…)為衍射階數;θm為第m個衍射階數的衍射角;λ為入射波長;d為柵板常數,這里柵板常數d固定為孔徑尺寸a的2倍,也就是d=2a.根據聲學理論[5],當單位振幅的平面波垂直入射于相位光柵時,全柵板角譜等于光柵透射率函數t的Fourier變換,衍射強度譜是Fourier變換F(t)的平方,柵板的透射率t(x)可以結合柵欄和孔徑的透射率得到.當平面波透過相位柵板時,柵板和孔徑的相位延遲分別為,其中:n,n分別為柵板和孔徑的衍射指數;H為柵12欄高度.因此,柵板透射率函數t(x)可以表示為

其中:n=0,±1, 2,….
根據t(x)的Fourier展開,得到,其中:則第n階衍射強度的角譜為

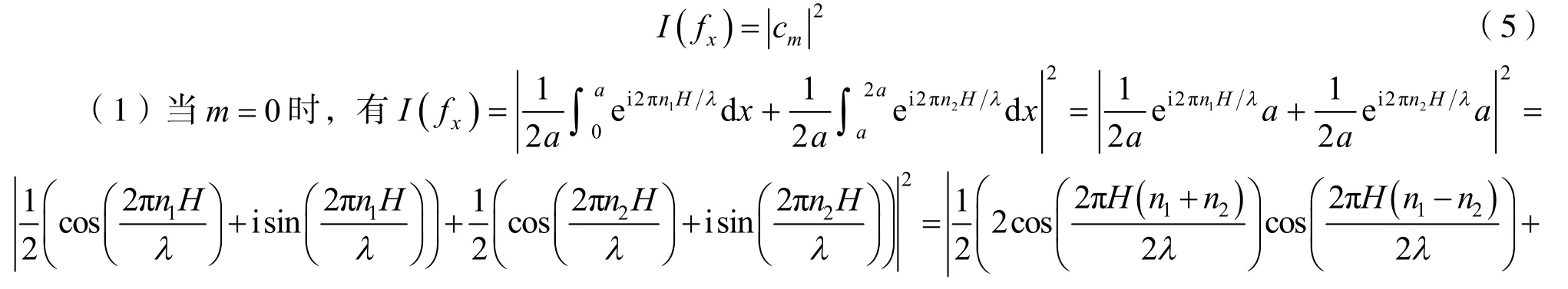

通過聲波的衍射強度的角譜方程,可以進一步研究聲波衍射的分布情況,從而設計人工超表面的分布結構.

