廣義積分的求解
2020-06-23 02:21:02高亮
高師理科學刊 2020年5期
關鍵詞:利用
高亮
(安徽國際商務職業學院 信息工程學院,安徽 合肥 231131)
廣義積分的定義與計算思維在整個數學知識構造中占據著非常重要的地位,不僅在無限函數求解上能夠帶來重要促進作用,在數理統計和微分方程等求解上也均有廣泛的應用[1].然而,廣義積分在實際應用中還存在較多問題,如概念抽象、函數形式多變和計算方法難以掌握等.如果僅通過定積分的計算思路進行求解,有可能對于大部分問題而言是行不通的,更難達到有效解決實際問題.因此,可以通過總結與深入研究特殊形式廣義積分計算方法,統籌對稱函數、可轉變函數等經常出現的積分形式,建立有效的計算體系.這樣不僅能夠幫助學生更快速地掌握解題的思路,還能夠檢驗運算過程合理性,對廣義積分求解的研究具有非常重要的實際意義.
1 廣義積分基本求法
由廣義積分的定義式可知,定積分的計算方法可以移植給廣義積分.于是,廣義積分計算中,同樣也有牛頓-萊布尼茨公式、換元積分法和分部積分法.
1.1 牛頓-萊布尼茨公式

1.2 換元積分法

1.3 分部積分法

2 廣義積分的特殊求法
對于廣義積分,一般計算方法只能夠解決部分函數計算,根據不同計算函數以及收斂情況可以相應地進行函數轉變,從而簡化計算過程,實現復雜函數積分的求解.如利用函數的對稱性、Γ函數和β函數、重要極限、留數定理、級數展開法以及含參變量積分等來計算.
2.1 利用函數的對稱性計算

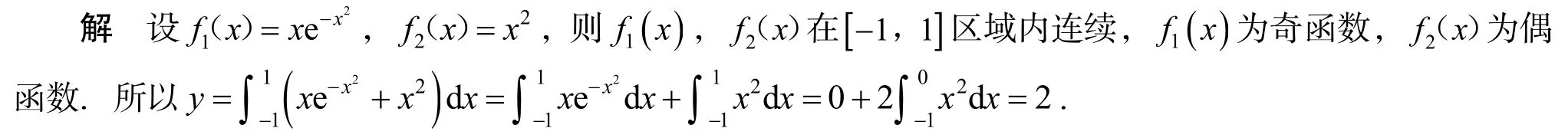
2.2 利用Γ,β函數計算

2.3 利用重要極限計算

2.4 利用留數定理計算

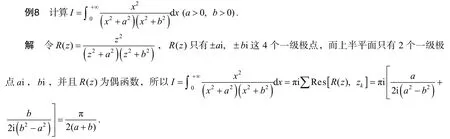
2.5 利用級數展開法計算
利用無窮級數計算廣義積分也是常用的一種技巧,可以將無窮區間上的廣義積分表示成級數形式來求積分.

2.6 利用含參變量積分計算

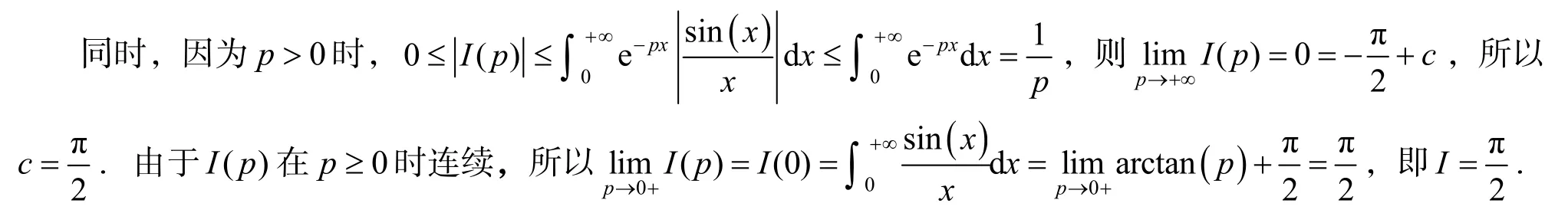
3 結語
綜上所述,廣義積分求法可以從不同的知識點、不同的角度去理解.針對不同的廣義積分,不僅可以使用換元積分求法和分部積分求法等基本方法,還可以利用函數的對稱性、Γ函數和β函數的性質、泰勒公式的展開等方法進行運算,深度挖掘與開發新方法解決廣義積分求解是當下研究熱點.然而,我們更應當學會選擇適當的方法來求解相應的廣義積分.
猜你喜歡
中等數學(2022年2期)2022-06-05 07:10:50
中學生數理化·七年級數學人教版(2021年11期)2021-12-06 05:38:48
中學生數理化(高中版.高考數學)(2021年6期)2021-07-28 06:19:08
小學生學習指導(低年級)(2020年6期)2020-07-25 02:31:36
小學生學習指導(低年級)(2019年11期)2019-11-25 07:31:44
小學生學習指導(低年級)(2018年9期)2018-09-26 05:59:44
瘋狂英語·新讀寫(2018年2期)2018-09-07 09:32:10
數學小靈通·3-4年級(2017年6期)2017-06-22 11:28:50
工業設計(2016年5期)2016-05-04 04:00:33
河北遙感(2015年4期)2015-07-18 11:05:06

