溫州市七都排水基地扇形建筑結構設計
黃顯學,范李劼,章增當,周增柱
(溫州設計集團有限公司,浙江 溫州 325000)
1 工程概況
本工程包括一棟業務綜合樓(1#樓,6層)和一棟防汛車庫物資用房(2#樓,2層),1#樓和2#樓之間通過鋼連廊連接,1#樓局部地下室(1層)作為設備用房。本工程用地面積12 898 m2,總建筑面積為11 219 m2,其中地上建筑面積10 982 m2,地下室面積237 m2,本文主要介紹1#樓結構設計。1#樓為扇形平面建筑,由弧形的6層主樓和扇形的1層裙房組成,主樓和裙房之間設變形縫分別進行結構設計。建筑效果圖見圖1。

圖1 建筑效果圖
1#樓主樓為丙類建筑,結構設計基準期50年,安全等級二級,抗震設防烈度為6度(0.05 g),設計地震分組為第一組,場地類別為Ⅳ類,特征周期0.65 s;地面粗糙度B類,50年重現期的基本風壓為0.6 kN/ m2。基礎采用φ600先張法預應力管樁,設計等級為丙級,以④-3層圓礫層作為樁端持力層。
2 結構體系及建模分析
1#樓主樓為多層建筑,采用現澆鋼筋混凝土框架結構及主次梁樓蓋體系,模型使用中國建筑科學研究院PKPMCAD工程部編制的結構分析程序《多層及高層建筑結構空間有限元分析與設計軟件SATWE》(2010-V4.3.4版)進行結構分析。
2.1 建模方向的確定及對比
1#樓主樓在建模時碰到模型方向的問題。將圓在坐標軸內分成四部分,為保持與建筑圖的一致性,模型建在坐標軸第三象限內,制圖方便;而根據高規[1]B.0.1-5條對扇形平面風荷載體型系數的規定,扇形對稱軸宜與X軸或Y軸重合,兩種方案方向差45°,見圖2。

圖2 模型方案
從體型上分析,模型第一平動會出現在圖2箭頭方向,宜將最弱軸調至X軸或Y軸,初步考慮采用第二種方案。現通過軟件將兩種方案建模后,對主要參數進行比較分析,兩種方案的參數見表1。

表1 不同方向模型計算指標對比
從表1可以得出以下結論:
1)兩種方案建模對周期基本無影響,兩個模型周期基本一致,各周期的方向角和最不利地震角相差約45°。
2)1#樓為多層框架結構建筑,對本樓而言,兩種方案建模對地震作用下位移角和位移比影響較小,“不利地震作用下最大位移角”兩個模型是一致的;抗規[2]規定框架結構6度區最大高度60 m,筆者將兩個模型樓層組裝至58.1 m,經分析得到各地震力作用下兩個模型位移角和位移比相差不大,針對高層及其他結構體型的建筑仍需進一步研究。
3)兩個模型的“風荷載作用下最大層間相對水平位移角”相差較大,尤其體現在弱軸方向,方案二Y向“風荷載作用下最大層間相對水平位移角”要比方案一小很多,SATWE僅計算X和Y兩個方向的風荷載,方案二更能體現結構薄弱面,當高層建筑由風荷載起控制作用時,應選擇方案二進行建模。
綜上所述,本次設計模型按方案二進行建模分析。
2.2 結構不規則分析
1#樓主樓存在以下幾項不規則項:1)扭轉不規則,最大位移比大于1.2;2)樓板局部不連續,2層樓面門廳大開洞,有效板寬38%小于50%。
針對上述不規則項采取的主要措施:1)對于扭轉不規則,加大兩端邊跨柱及梁截面使周期比滿足控制在0.88,并考慮偶然偏心計入雙向地震的影響,結構計算時采用空間結構計算模型并計入雙向水平地震作用下的扭轉影響;2)為削弱樓板開洞的不利影響,將2層樓板加厚,雙層雙向配筋,同時,計算中考慮彈性板,以準確分析樓板削弱處周圍構件的內力,確保洞口周邊構件的設計安全。另外,筆者使用中國建筑科學研究院PKPMCAD工程部編制的結構分析程序《復雜多層及高層建筑結構空間有限元分析與設計軟件PMSAP》(2010—V4.3.4版)進行結構指標校核,見表2。

表2 不同軟件模型計算指標對比
通過兩個不同力學模型的計算軟件分析,計算結果相近,各項指標滿足規范要求(考慮偶然偏心的地震作用下最大扭轉位移比均小于1.4),模型及計算結果合理有效,計算模型符合結構實際工作狀況,計算結果可以作為工程設計的依據。
表3為模型各樓層受剪承載力及承載力比值,表中數據顯示各樓層受剪承載力均大于其相鄰上一層受剪承載力的80%,不存在抗剪薄弱層,屬于承載力變化規則的結構;圖3為模型樓層剛度比,各層剛度比比值滿足規范限值要求。因此,2層大開洞處抗側剛度無明顯突變,對整體影響較小。

表3 樓層剛度比
說明:Ratx1,Raty1(剛度比1):X、Y方向本層塔側移剛度與上一層相應塔側移剛度70%的比值或上三層平均側移剛度80%的比值中之較小值(按抗規3.4.3;高規3.5.2-1)。
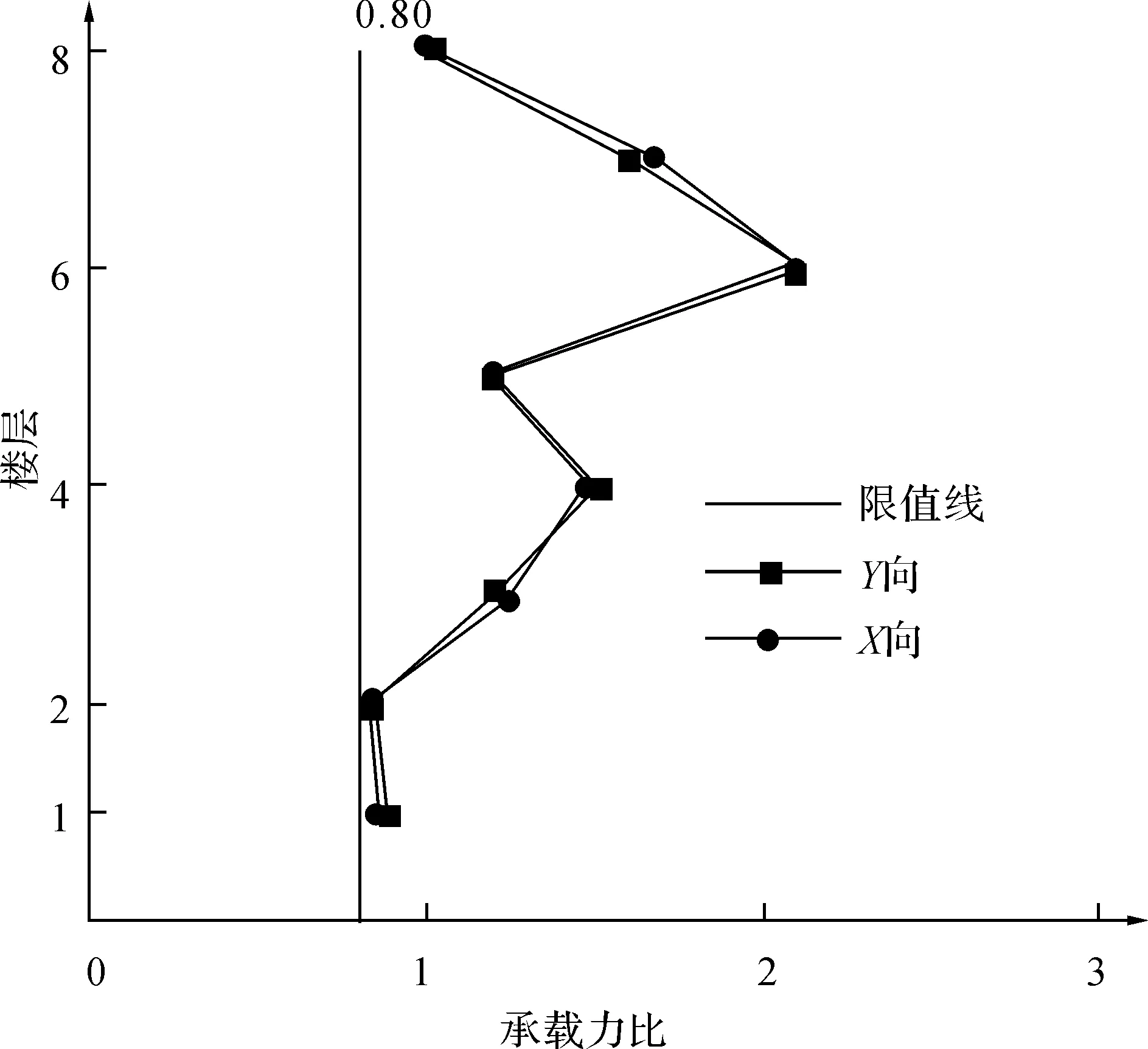
圖3 多向受剪承載力比簡圖
3 混凝土和鋼筋用量分析
分別從板、梁和柱三方面定性分析1#樓主樓混凝土和鋼筋用量:1)扇形平面內圈弧長小外圈弧長大,因此靠近外圈的房間板跨大板厚也大,本次設計一般用房外圈板厚取110 mm,內圈板厚取100 mm,板混凝土用量會較矩形平面混凝土用量大;2)扇形截面存在大量弧形梁,弧形梁軟件默認梁抗扭折減系數為1.0,有樓板的普通梁抗扭折減系數為0.4,因此為滿足弧形梁抗扭要求,建模時梁寬會加大且梁抗扭筋也會加大,梁混凝土和鋼筋用量均較矩形平面的混凝土和鋼筋用量大;3)有凹角的建筑容易聚風,在風荷載體型系數取值上,扇形平面根據高規[1],體型系數統一取到最不利值1.5,一般的矩形平面取到1.3,規范[3]規定超過45 m的矩形平面體型系數取到1.4均比1.5小,當結構受風荷載控制時扇形平面受荷載作用更大,結構梁柱混凝土及鋼筋用量均會比矩形平面用量大。
筆者將扇形截面換算成等面積矩形截面進行建模分析并進行工程量統計對比。假設扇形平面內徑為r,外徑為R:
矩形平面寬B=(R-r);
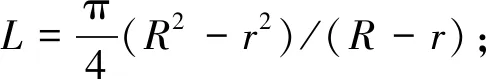
再將矩形長9等分布置柱網,柱截面和梁截面與原扇形模型一致,板厚按需要布置,矩形平面布置圖見圖4。經計算,模型指標參數和配筋滿足規范要求,對扇形模型和矩形模型分別進行結構工程量統計,結果見表4。
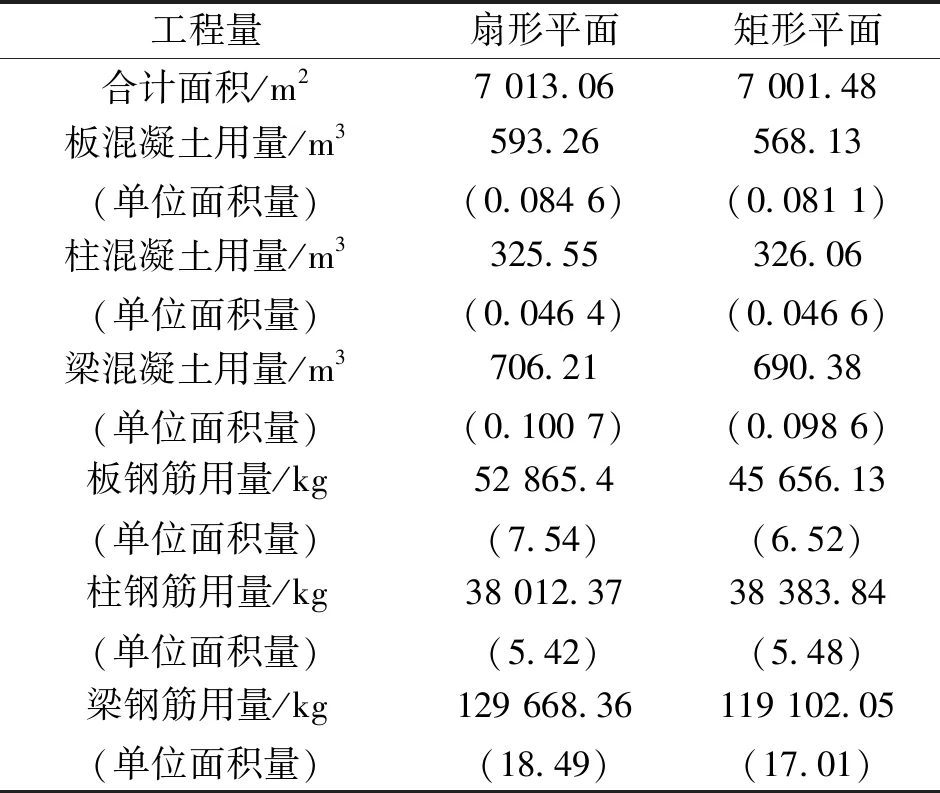
表4 工程量統計
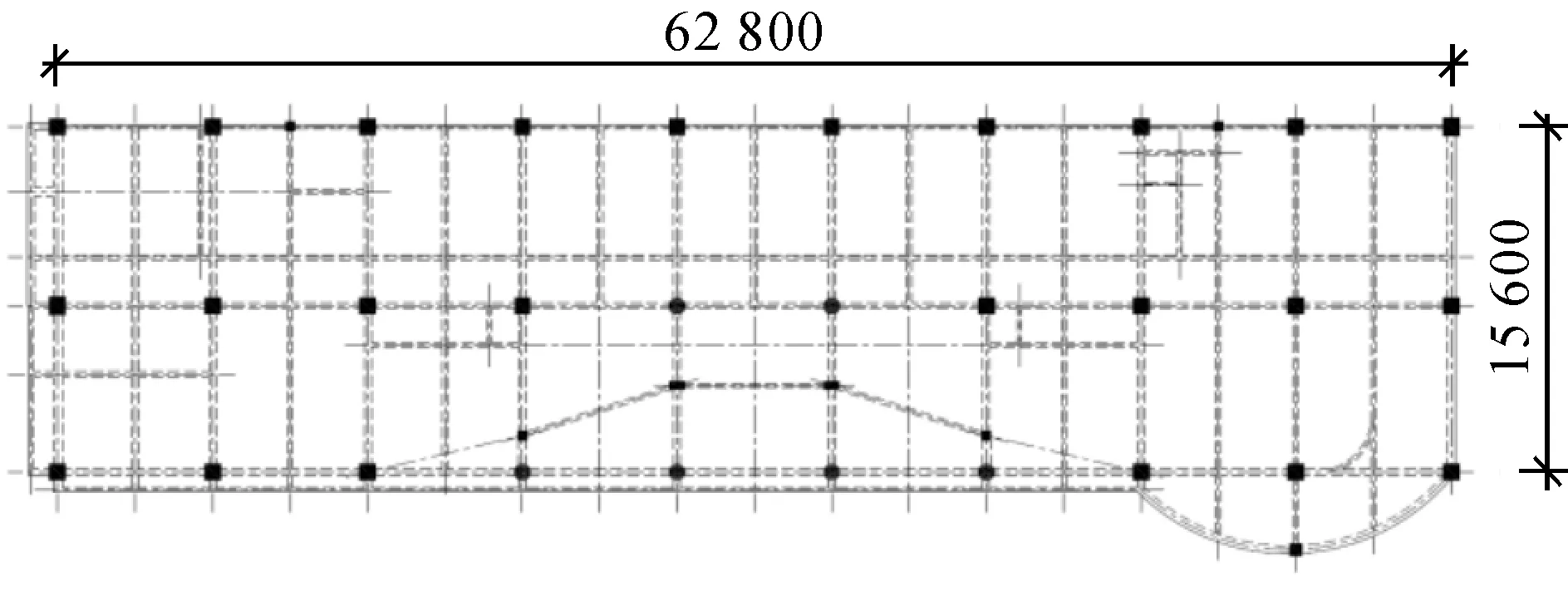
圖4 矩形平面布置圖
通過工程量統計對比,兩個模型柱截面是一致的,因此當矩形平面面積小時,柱混凝土和鋼筋含量比扇形平面微高一點;對于梁板的混凝土和鋼筋含量,矩形平面比扇形平面小,尤其鋼筋含量差距更大。模型統計結果與定性分析基本保持一致,因此在造價方面,矩形平面比扇形平面省。
4 結 語
通過對1#主樓扇形平面,多層現澆框架結構的建模和研究得出以下幾點結論:
1)扇形平面采用PKPM建模時,宜將扇形對稱軸放置在X軸或Y軸,使得風荷載作用下指標和構件受力更準確。
2)扇形平面弧長較徑向方向長,可以采用加強邊跨結構構件的方法抗扭;對于門廳大開洞,可以采取加強板并雙向雙層配筋的方法加強該樓層整體性。
3)在同等條件下,扇形平面比矩形平面的混凝土和鋼筋用量更多,費用更高,如想節省造價不宜采用扇形平面。
4)其他結構體系及高層建筑的扇形平面,需另外研究。

