獨塔雙索面混凝土斜拉橋地震響應分析

莫海洪，饒梓彪

（中交第四航務工程勘察設計院有限公司，廣東 廣州 510230）

0 引言

近年來，除了當前尚處于研究和爭論狀態的基于失效概率的地震功率譜抗震設計和虛擬激勵分析法外，基于靜態水平力加載的加速度反應譜方法和基于動力學基本規律的時間歷程分析法是當前橋梁工程抗震設計中普遍應用的兩種成熟設計方法[1-2]。反應譜方法通過分析結構本身的振動特性，將實際復雜結構抽象為一個具有有限自由度的力學模型，并基于矩陣解耦的數學方法，將多自由度系統分解為一組具有統計相關性的單自由度系統。通過理論解析技術分別計算得到每個單自由度系統的動力學響應后，再將各單自由度系統的響應結果進行統計學疊加，作為整體結構在地震作用下的最終響應結果；地震時間歷程動力分析法對計算時間間隔進行離散，并在每個離散的時間步長內對結構應用動力學基本方程進行動力響應計算[3-4]。時間歷程動力分析法是到目前為止計算地震動力響應的最完整分析方法，該方法可以在計算過程中考慮各種不同的非線性動力學效應，但由于運算過程的復雜性和計算資源的開銷巨大，因此時間歷程分析法一般只是作為反應譜分析的驗證手段[5-6]。

本文以酉水三橋為依托工程，對其動力特性及抗震性能進行了分析。如前所述，為校驗分析方法和分析結果的準確性，計算分別采用加速度反應譜分析法與時間歷程分析法進行獨立計算并比對計算結果[7]。地震響應計算主要針對橋體主墩和橋身主梁的特征截面進行地震響應分析，并將基于數值分析得到的結構響應結果與CJJ 166—2011《城市橋梁抗震設計規范》[8]中所推薦的擬靜力方法計算結果進行比較，從而全面評估橋梁在地震作用下的結構可靠性。本文研究的中間數據與所得到的結論對于其他橋梁工程的抗震評估具有一定的參考價值。

1 工程概況

酉水三橋全長417 m。其中橋體主結構為獨塔雙索面斜拉橋，橋梁主墩和主梁之間設計為固結傳力模式。橋梁主體斜拉部分的跨徑長度組合為196 m+101 m+62 m，引橋采用2×25 m 小箱梁，橋面寬度設計為29.5 m。橋梁主塔結構設計為鉆石形，橋體主梁結構設計為三室單箱預應力混凝土結構，斜拉索布置設計為扇形。主橋結構立面如圖1 所示[9]。

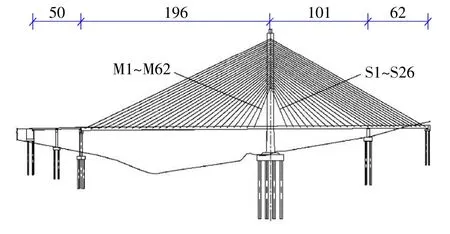
圖1 橋梁立面布置圖（m）Fig.1 Elevation layout of bridge(m)

2 抗震設防標準及結構抗震性能目標的確定

根據GB 18306—2015《中國地震動參數區劃圖》[10]及 JTG B02—2013《公路工程抗震規范》[11]中對于地震場地分類的相關規定：通過前期工程地質勘察，可以判斷工程場地土類型屬中硬土，場地類別歸屬為Ⅱ類，工程場地的地震基本烈度為6 度，對應的地震動峰值加速度為0.05g，場地特征周期值為0.35 s，綜合信息表明，工程場地屬于地震不利區。本文依托工程所處的場地在不同超越概率條件下對應的地表水平加速度峰值如表1 所示。

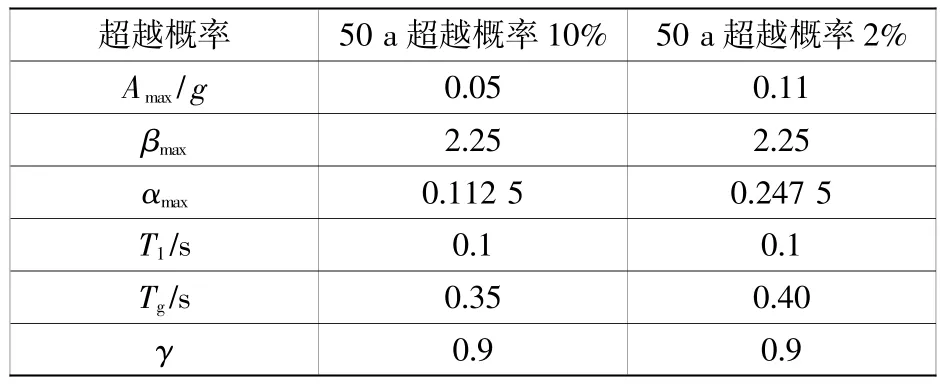
表1 工程場地地表設計地震動參數Table 1 Design ground motion parameters of engineering site

根據《城市橋梁抗震設計規范》[8]中的相應規定：對于斜拉索結構的市政類橋梁，其抗震設防級別應設置為甲級，其抗震標準應高于基本場地烈度1 度，因此考慮橋梁結構的抗震設防標準應當有所提高，見表2。

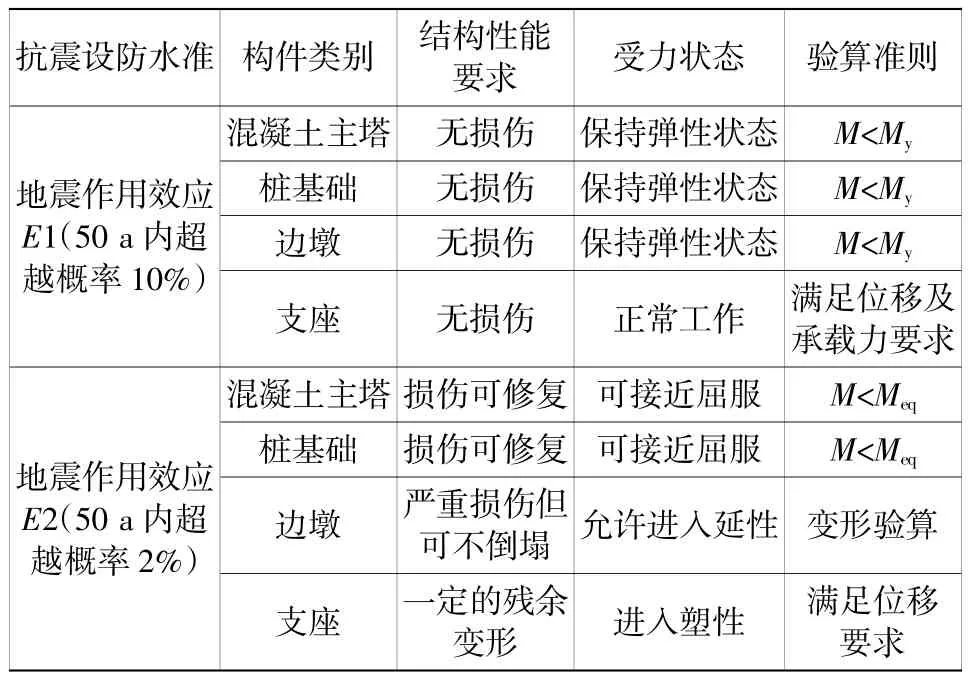
表2 橋梁主體結構的抗震設防標準與性能目標Table 2 Seismic fortification standards and performance objectives of bridge main structure

3 計算模型與動力特性

3.1 計算模型

計算分析采用MIDAS 橋梁結構專用有限元程序軟件。采用空間梁單元模擬橋梁結構的橋墩、主梁和主塔結構，采用桁架單元模擬斜拉索對主梁的連綴效應，并以此模型為基礎，開展橋梁整體結構在地震作用下的動力響應評估。

3.2 邊界條件

本橋成橋狀態結構邊界條件邊、中支點支座模擬彈性連接，考慮交界一聯橋梁剛度邊界條件影響，樁基礎采用“m”法土彈簧模擬[12-13]。

3.3 動力特性

采用多重Ritz 法對全橋動力特性進行分析，成橋狀態振型特點見表3。

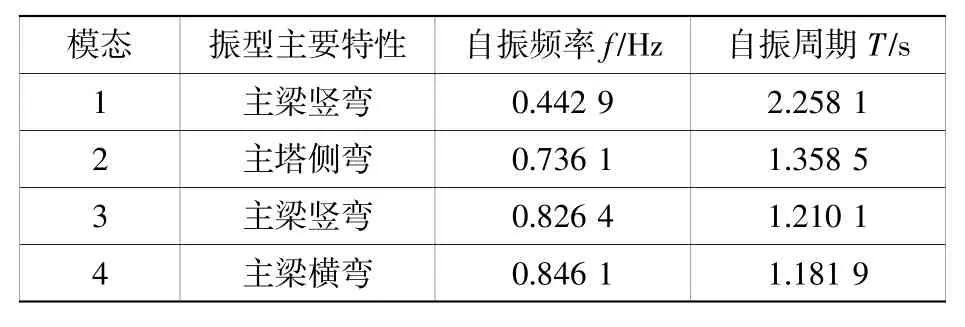
表3 成橋狀態結構動力特性Table 3 Dynamic characteristics of bridge structure

4 地震反應譜分析

4.1 結構時間歷程分析

與加速度反應譜分析類似，時間歷程分析中的地震動輸入采用水平縱向+豎向以及水平橫向+豎向兩種組合方式。

根據《城市橋梁抗震設計規范》[8]中的相關規定，在考慮豎向地震加速度的組合作用下，豎向加速度峰值取為水平向加速度峰值的2/3。為盡可能消除時間歷程計算結果的隨機性，主橋結構的地震響應計算結果取3 組隨機地震波作用結果的最大值。基于上述計算條件，橋梁主體結構在E2地震作用下的位移響應如表4 所示，橋梁主塔結構的控制截面的地震響應結果如表5 所示（僅列舉E1 地震作用下的響應結果）。

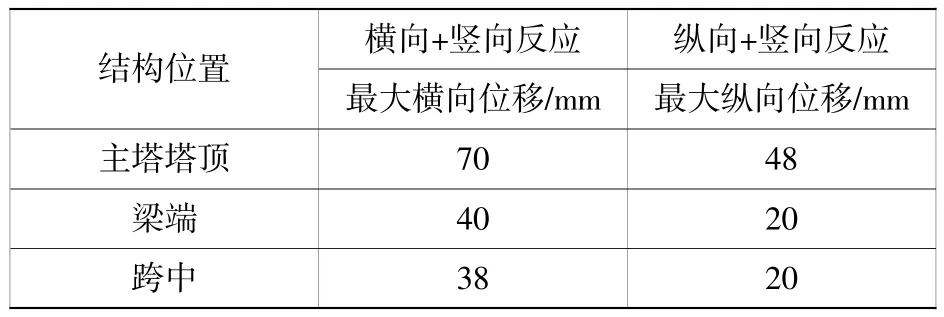
表4 橋梁控制點處地震位移響應（E2 地震作用）Table 4 Seismic displacement response at bridge control point(E2 seismic action)

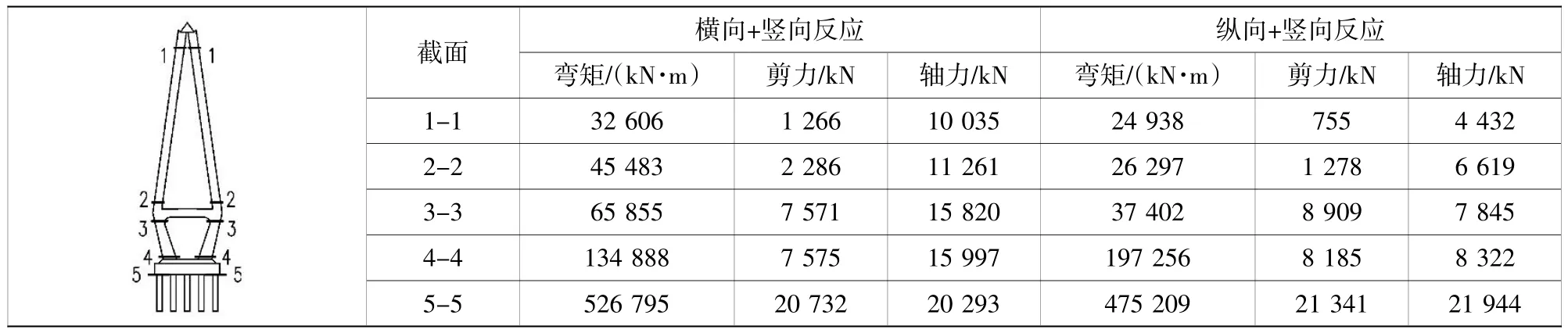
表5 主塔結構（控制截面處）地震響應（E1 地震作用）Table 5 Seismic response of main tower control section(E1 seismic action)

4.2 結構反應譜分析

根據《城市橋梁抗震設計規范》[8]中的相關規定，采用加速度反應譜進行地震響應分析時，所選用的加速度反應譜為Sa（T）=Amaxβ（T），其中：β為加速度放大系數譜，是場地周期T 的函數；βm為加速度放大系數的最大值；Tg為工程場地的特征周期，s；γ 為反應譜下降段的衰減指數，當系統阻尼比為0.05 時，該值為0.9；Amax為場地的地面加速度峰值。本文計算所采用的參數見表6。

抗震分析中通常需要考慮水平方向的地震加速度與豎直方向地震加速度的聯合作用。水平向的地震作用通常按照縱向和橫向分開考慮，因此地震激勵的輸入方式分為兩種：1）水平縱向+豎向； 2）水平橫向+豎向，不同方向地震作用結果采用SRSS 法組合。

表6 場地水平向設計反應譜特征參數（阻尼比5%）Table 6 The characteristic parameters of horizontal design response spectrum of site(damping ratio 5%)

對于地震響應分析而言，需要確保有足夠多的模態參與到計算中，從而避免遺漏重要的結構響應。通過試算可以確定前150 階振型在各自由度上的質量參與系數均達到95%以上。不同振型計算結果采用CQC 法組合。從結構反應譜分析與結構線性時程分析兩種方法計算得到的結果比對可以看到：不管是對于結構位移響應還是結構內力響應，反應譜法和時間歷程法的計算結果都較為接近，總體而言，時間歷程法計算結果在量值上偏大，兩者相對誤差不大于20%。

4.3 結構抗震驗算

通過以上分析可以看到：時間歷程分析法的計算結果相對加速度反應譜方法的計算結果略大，因此本節采用線性時程分析法的計算結果對結構抗震性能進行校驗，以判斷結構是否滿足抗震性能規定。

鋼筋混凝土截面等效屈服彎矩在實際加載過程中并無明顯的指標可供參考，在實際實施過程中通常將實際的截面彎矩-曲率曲線等效為一個彈塑性曲線。對應的等效屈服彎矩Meq計算如圖2由陰影部分面積相等求得。其中My為截面在指定軸力作用下的外層鋼筋屈服時所對應的彎矩；Meq=My為所對應的等效屈服彎矩；Mu對應指定軸力作用下的截面抗彎承載力。基于上述方法，主塔的抗震驗算結果見表7。

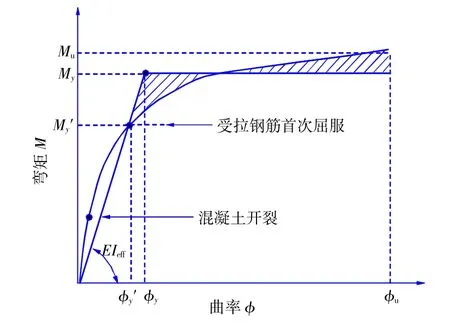
圖2 等效屈服曲率和屈服彎矩計算圖示Fig.2 Calculation diagram of equivalent yield curvature and yield moment

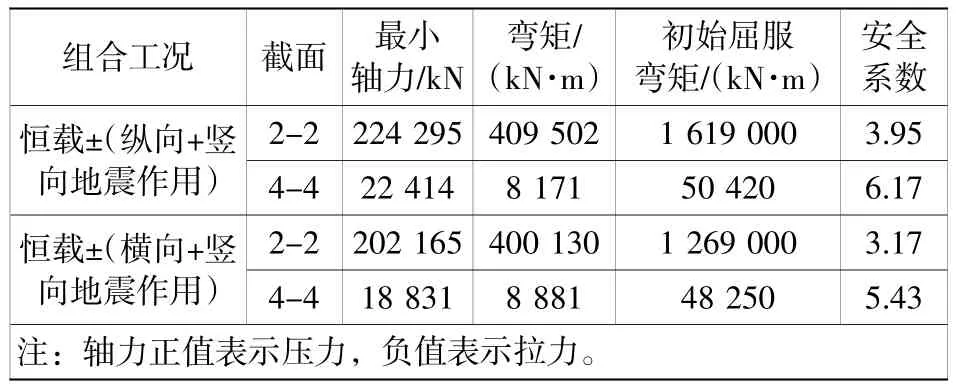
表7 最不利軸力下主塔初始屈服彎矩驗算（E2 地震作用）Table 7 Checking calculation of initial yield moment of main tower under the most unfavorable axial force(E2 seismic action)

從表中可以看到：在E2 地震荷載作用下，橋梁主塔結構最不利截面彎矩安全系數均大于1，說明橋梁主塔結構僅發生可輕微損傷，滿足抗震性能要求。

5 結語

本文以酉水三橋為依托工程，同時采用結構反應譜分析與結構線性時程分析對主塔、主梁控制截面進行了抗震分析，并以規范中的橋梁結構抗震性能目標為參考，對兩種計算方法的計算結果進行比對與分析，研究得出以下結論：

1）采用結構反應譜分析與采用線性時程分析兩種方法得到的結果之間吻合較好，主橋采用墩塔梁固結體系，結構抗震性能可靠。

2） 在50 a 內超越概率為10%的地震荷載作用下，橋梁主塔結構的最不利截面彎矩均小于截面初始屈服彎矩，因此橋梁在地震作用下保持在彈性范圍之內，可以充分滿足地震環境下的抗震性能要求。

3）在50 a 內超越概率為2%的罕遇地震荷載作用下，橋梁主塔結構最不利截面的彎矩安全系數均大于1，說明橋墩和樁基在地震作用下的損傷可修復，可以滿足罕遇地震環境下的抗震性能要求。