強降雨入滲下臨海軟土開挖邊坡穩(wěn)定性分析

黃泰坤，王元戰(zhàn)，姜金勇，賈晗，劉少增

（1.天津大學建筑工程學院，天津 300072；2.中交第一航務(wù)工程勘察設(shè)計院有限公司，天津 300222；3.南通港集團建設(shè)投資有限公司，江蘇 南通 226000）

0 引言

近年來我國頻繁遭遇強降雨等極端天氣，由此引發(fā)了較多的滑坡災害事故[1-3]。季節(jié)性集中降雨具有強度大、持時長、次數(shù)多等特點，從而導致滑坡多，災害重，產(chǎn)生嚴重的社會影響。工程中缺乏考慮強降雨對邊坡穩(wěn)定安全系數(shù)計算方法，常忽視降雨對邊坡的影響，由于未采取排水措施，常在開挖交界面處出現(xiàn)開裂、沖溝等現(xiàn)象，嚴重影響了整體邊坡的穩(wěn)定性。

在強降雨過程中，土體內(nèi)部多因素復雜的相互作用，土坡穩(wěn)定性問題引起了工程師和學者的廣泛關(guān)注。目前眾多文獻[4-10]集中于對原狀邊坡的原位浸水測試和增濕影響的室內(nèi)試驗；文獻[11-15]采用數(shù)值方法和試驗方法研究了路基邊坡在雨水入滲后的開裂變形問題；文獻[16-17]對某填溝造地工程進行了原位監(jiān)測研究，表明地表積水和降雨影響入滲可達7 m 之多，但未對其他災害現(xiàn)象進行探討。上述研究黃土邊坡、路基開挖中應(yīng)用較多，為邊坡理論和工程設(shè)計提供了大量支撐。然而針對軟土、大面積開挖在強降雨入滲作用下邊坡穩(wěn)定性及其工程應(yīng)用研究不多，其防控的設(shè)計方法與技術(shù)措施鮮有報導。

鑒于此，本文以某軟土開挖工程實際為背景，基于ABAQUS 有限元軟件平臺，建立了工程區(qū)域非飽和土滲流-應(yīng)力耦合模型，研究強降雨入滲邊坡穩(wěn)定性的影響及變形規(guī)律，為類似項目設(shè)計理論和工程措施提供一種很好的展示。

1 工程背景

某堿廠排渣場位于濱海淺灘邊上，工程竣工后經(jīng)多年堿渣堆積形成現(xiàn)有堿渣山，隨著環(huán)保的加強及港口開發(fā)的需要，急需對堿渣山搬遷治理，設(shè)計方案為開挖填埋堿渣。納渣區(qū)選址于堿渣山北側(cè)大面積淺灘區(qū)域，場地標高+3.5 m，開挖底標高為-10.0 m，設(shè)計邊坡1:3～1:4，開挖面積約70 萬m2。設(shè)計了多級馬道開挖（圖1）。開挖深度大、土質(zhì)軟、后方堆載高堿渣山，施工過程需經(jīng)強降雨期，為確保邊坡安全，對降雨入滲下軟土開挖邊坡整體穩(wěn)定性進行研究。

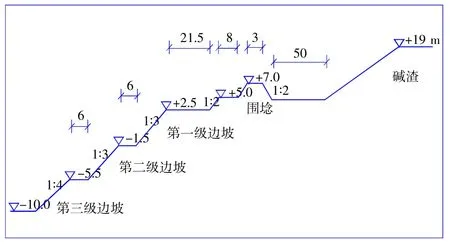
圖1 軟土開挖、后方圍埝和已堆載的堿渣斷面圖Fig.1 Cross-section of soft soil excavation,rear enclosure and loaded slag

2 有限元數(shù)值模型建模方法

2.1 本構(gòu)模型

土體本構(gòu)模型采用Mohr-Coulomb 模型。

Mohr-Coulomb 準則是根據(jù)材料發(fā)生破壞時的應(yīng)力Mohr 圓得到的，破壞線是與Mohr 圓相切的直線，Mohr-Coulomb 準則可表示為式（1）：

式中：τ 為材料的剪切強度；σ 為該點的應(yīng)力；c為材料的黏聚力；φ 為材料的內(nèi)摩擦角。

Mohr-Coulomb 準則采用應(yīng)變不變量表示時屈服面方程為式（2）～式（4）：

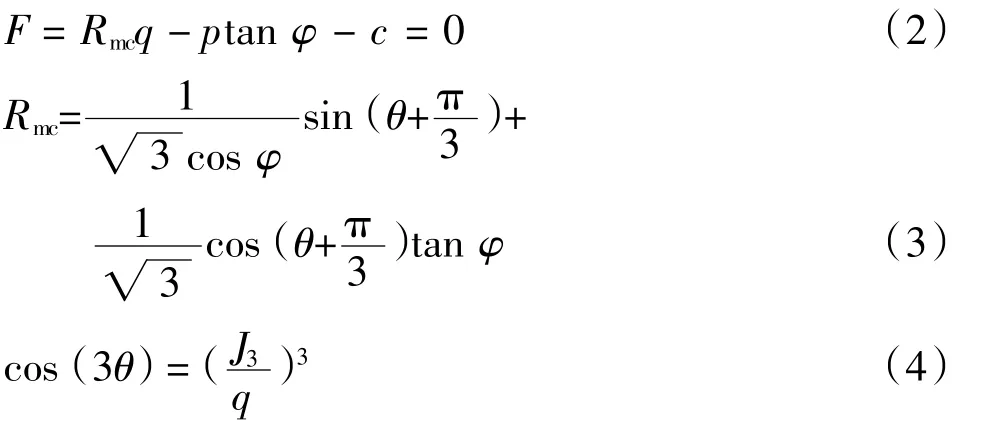
式中：p 為球應(yīng)力；q 為廣義剪應(yīng)力；φ 為巖土體材料的內(nèi)摩擦角，取值范圍為[0，90°）；c 為土體黏聚力；Rmc（θ，φ）為M-C 偏應(yīng)力系數(shù)，它決定平面內(nèi)的屈服面形狀；θ 為極偏角；J3為第三偏應(yīng)力不變量。

2.2 非飽和滲流

飽和土體采用常規(guī)達西滲流理論。非飽和土中，由于有水和氣兩種流體存在于滲流中，與飽和土的流動性質(zhì)不同。Richards[18]于1931 年忽略氣體流動阻力，將Darcy 定律推廣到非飽和土，該定律采用層流式的Darcy 定律表示，如式（5）：

式中：θw為含水率；k（θw）為某一體積下含水率 θw的非飽和土滲流系數(shù)。

在非飽和土體中，由于部分孔隙水被氣體所填充，其滲透性小于飽和透水性，同時，又由于受土體含水率、飽和度或孔隙比變化影響，因此將滲透系數(shù)表示為基質(zhì)吸力、飽和度S 和體積含水量 θw的函數(shù) k（θw）。

2.3 降雨入滲模型

降雨入滲的過程復雜，Mein 和Larson[19]采用由降雨強度q、土壤允許入滲的容量fp、土壤飽和時的滲透系數(shù)ks等3 個因子來描述降雨入滲的過程與行為：

1）q ＜ks時，地表徑流不會發(fā)生，降雨將全部入滲，此時水的入滲率保持不變。

2）fp＞q≥ks時，所有的雨水全部入滲，隨著入滲深度的增加而變小，但此時降雨強度還未達到土壤允許入滲的容量，故入滲率并不會降低，且入滲率很高。

3）q≥fp時，由于降雨強度大于土壤的入滲容量，故部分降雨并不入滲，形成地表徑流，而入滲率在降雨達到入滲容量后，將逐步下降。

所以，降雨入滲過程可以分成為2 個階段，第一階段稱為供水控制階段，第二階段稱為土壤入滲率控制階段。2 個階段的交點稱為積水點。前一階段稱為無壓入滲或自由入滲，后一階段稱為積水或有壓入滲。本文中，降雨考慮為強降雨情況（＞10 mm/h），遠大于土體滲透能力，因此，本模型中的降雨入滲為“積水模型”或有壓入滲，即第3 種情況。

2.4 強度折減法

強度折減法SSRT（Shear Strength Reduction Technique）最早由 Zienkiewicz 等[20]提出，后被許多學者廣泛采用。當假定邊坡內(nèi)所有土體抗剪強度的發(fā)揮程度相同時，這種抗剪強度折減系數(shù)相當于傳統(tǒng)意義上的邊坡整體穩(wěn)定安全系數(shù)Fs，又稱為強度儲備安全系數(shù)，與極限平衡法中所給出的穩(wěn)定安全系數(shù)在概念上是一致的。

折減后的抗剪強度參數(shù)可分別表達為式（6）、式（7）。

式中：c 和φ 為土體所能提供的抗剪強度；cm和φm為維持土體平衡所需要的或土體實際發(fā)揮的抗剪強度；Fr為強度折減系數(shù)。

計算中假定不同的強度折減系數(shù)Fr，根據(jù)折減后的強度參數(shù)進行有限元分析，觀察計算是否收斂。整個計算過程中不斷的增加Fr，當達到臨界破壞時的強度折減系數(shù)Fr就是邊坡穩(wěn)定安全系數(shù)Fs。

3 有限元數(shù)值模型建立與驗證

3.1 模型構(gòu)建

根據(jù)上述模型建立方法建立本工程有限元二維邊坡穩(wěn)定性分析模型（圖2）。其中，模型底部為固定位移約束（U1=U2=0），兩側(cè)為水平位移約束（U1=0）；模型兩側(cè)的孔壓按靜水水壓條件布置，左側(cè)水位標高為-10 m，右側(cè)水位標高為+3.5 m。圖2 中的圍埝為碾壓黏土，堿渣山為堿渣，土體自上而下分別為：淤泥質(zhì)粉質(zhì)黏土、淤泥質(zhì)黏土、淤泥、粉質(zhì)黏土、粉土、粉質(zhì)黏土和粉土，在圖2 中用不同顏色標記。土體的本構(gòu)模型采用Mohr-Coulomb 模型，孔隙水流動按擴展的非飽和達西定律考慮。

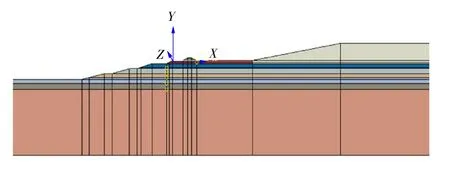
圖2 有限元模型Fig.2 Finite element model

土層分布以及土體材料參數(shù)如表1 所示。

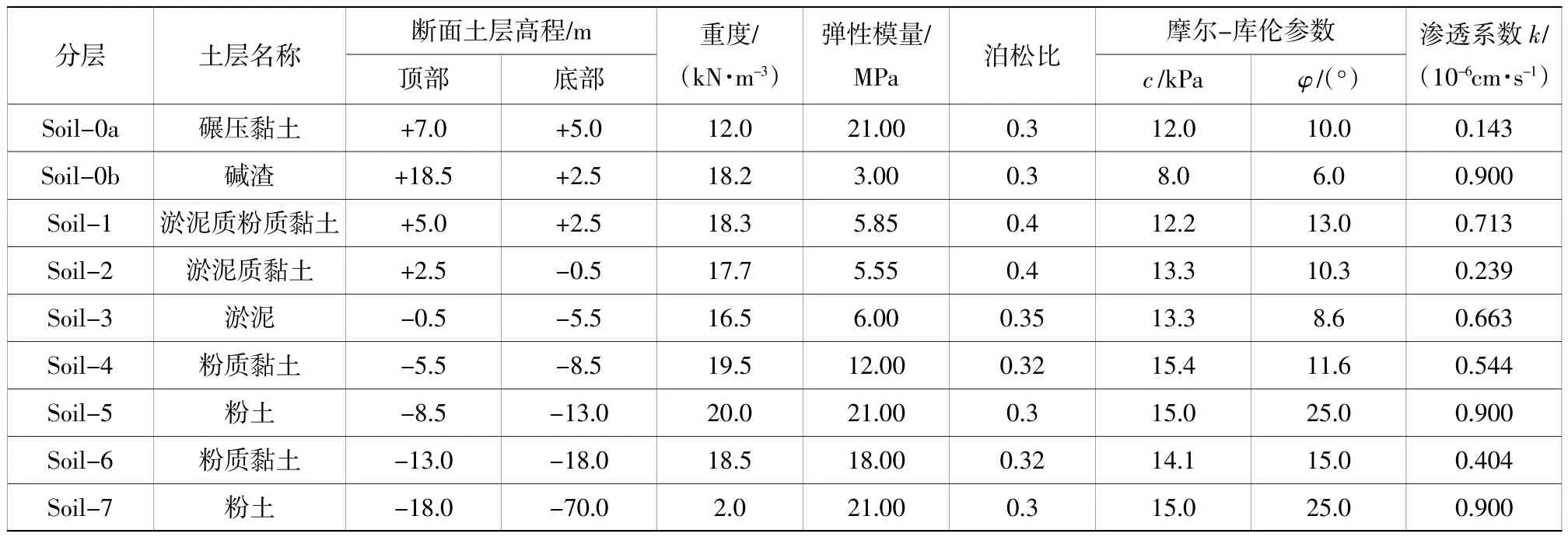
表1 土層分布及土體材料參數(shù)Table 1 Soil layer distribution and soil material parameters

3.2 模型驗證

圖3 為野外現(xiàn)場一級開挖斷面（坡肩）處的監(jiān)測水平位移與有限元計算結(jié)果對比。有限元計算結(jié)果與監(jiān)測數(shù)據(jù)相比略大，但總體上得出的計算結(jié)果和監(jiān)測數(shù)據(jù)較為接近。

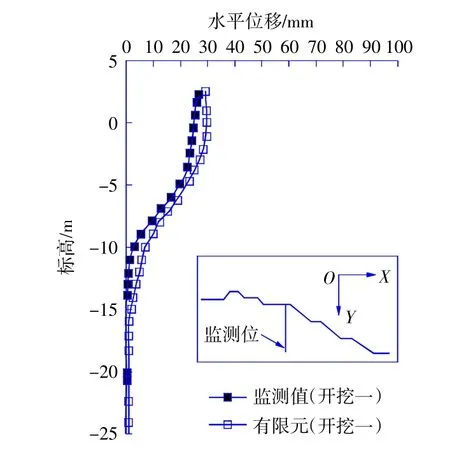
圖3 有限元計算結(jié)果與現(xiàn)場監(jiān)測數(shù)據(jù)的對比Fig.3 Comparison between the results of FEA and field monitoring date

圖4 為未考慮雨水入滲影響下，GEO-SLOPE軟件的極限平衡法邊坡穩(wěn)定性計算結(jié)果，其中，水位考慮為兩段折線，土層參數(shù)與有限元模型中的設(shè)置一致。計算結(jié)果表明，最不利邊坡安全系數(shù)為1.657，與本文建立的有限元計算結(jié)果1.70相近。

圖4 GEO-SLOPE 極限平衡法邊坡穩(wěn)定性Fig.4 Slope stability of limit equilibrium method based on GEO-SLOPE

4 有限元數(shù)值模型應(yīng)用

4.1 模型設(shè)置

基于實際開挖工程，分別研究常規(guī)不考慮強降雨影響、考慮強降雨入滲影響的開挖邊坡穩(wěn)定性。模型設(shè)計2 種工況，即工況一：不考慮雨水入滲影響；工況二：考慮強降雨入滲影響。

4.2 模擬結(jié)果

4.2.1 不考慮雨水入滲（工況一）

圖5 為開挖邊坡頂處位移與折減系數(shù)的關(guān)系曲線。從圖中可以看出，無論是哪一種失穩(wěn)準則，工況一的安全折減系數(shù)都為1.70。

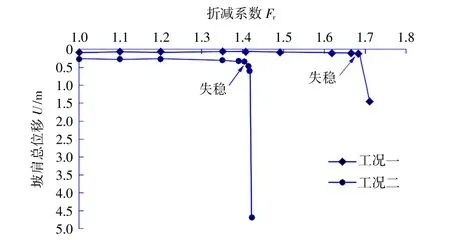
圖5 U-Fr 曲線圖Fig.5 U-Fr curve

圖6 為不考慮雨水入滲影響下的邊坡穩(wěn)定（工況一）的孔隙水壓力POR（總孔壓）、土體飽和度SAT、土體水平位移U1、豎向位移U2，以及破壞時的塑性應(yīng)變PEMAG 變化特征圖。

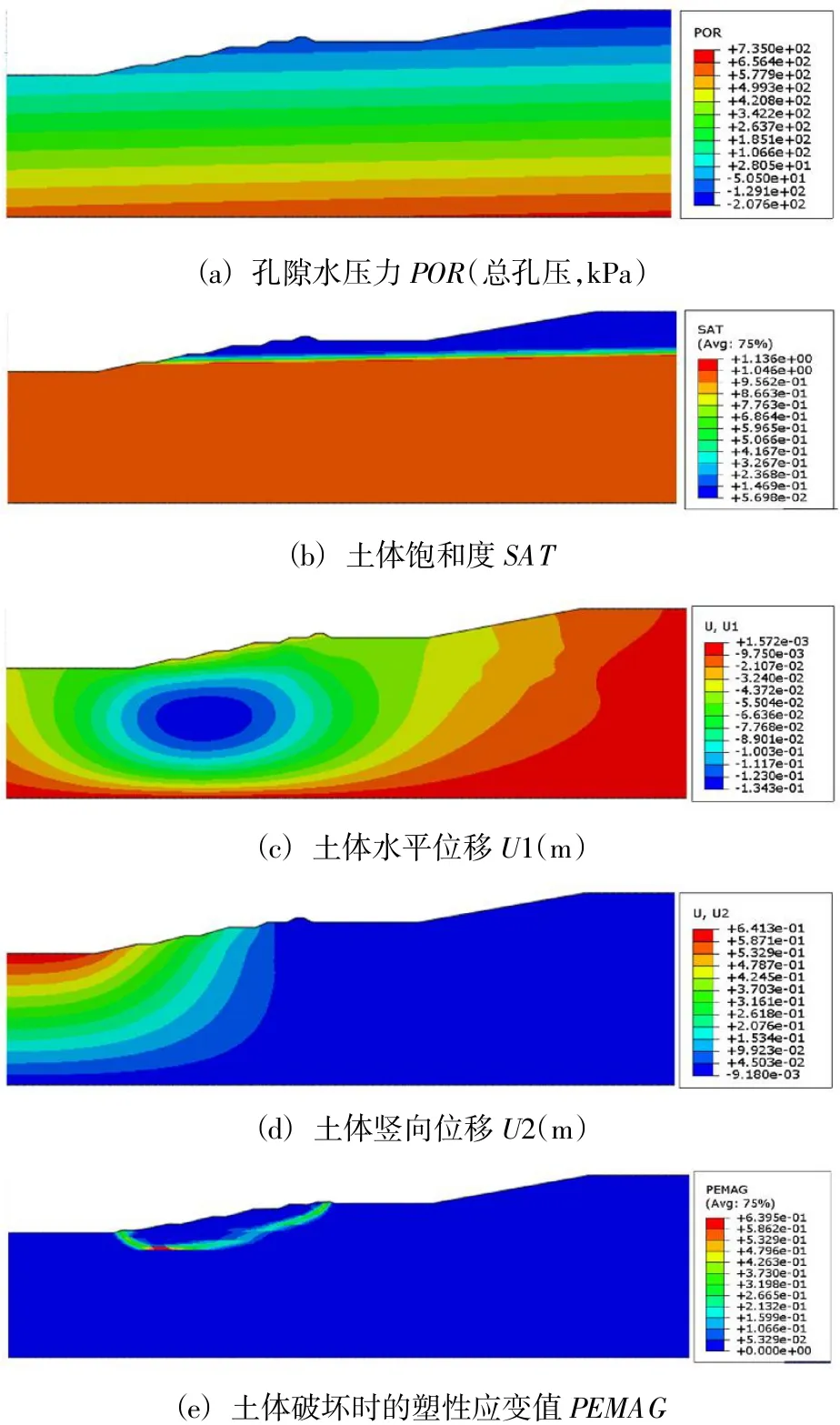
圖6 工況一邊坡響應(yīng)特征圖Fig.6 Response characteristic of slope of condition 1

如圖6 所示，未折減之前，邊坡頂處土體水平、豎向位移分別為-0.030 m、+0.067 m，在達到滑移破壞階段，二者位移分別達到-1.35 m 和-0.56 m。從破壞時塑性應(yīng)變圖可以看出，未考慮雨水入滲，滑裂面滑出點位于坡底-10 m 位置。

4.2.2 考慮強降雨入滲（工況二）

圖5 為開挖邊坡頂處位移與折減系數(shù)的關(guān)系曲線。從圖中可以看出，無論是哪一種失穩(wěn)準則，工況二的安全折減系數(shù)都為1.42。

圖7 為考慮雨水入滲影響下的邊坡穩(wěn)定（工況二）的孔隙水壓力POR（總孔壓）、土體飽和度SAT、土體水平位移U1、豎向位移U2，以及破壞時的塑性應(yīng)變PEMAG 變化特征圖。如圖所示，未折減之前，邊坡頂處土體水平、豎向位移分別為-0.250 m、+0.087 m，在達到滑移破壞階段，二者的位移分別達到-4.48 m 和-1.38 m。考慮雨水入滲，滑出點位于坡面-5.5 m 位置，較工況一有所抬高，提示坡面可能出現(xiàn)破壞情況。

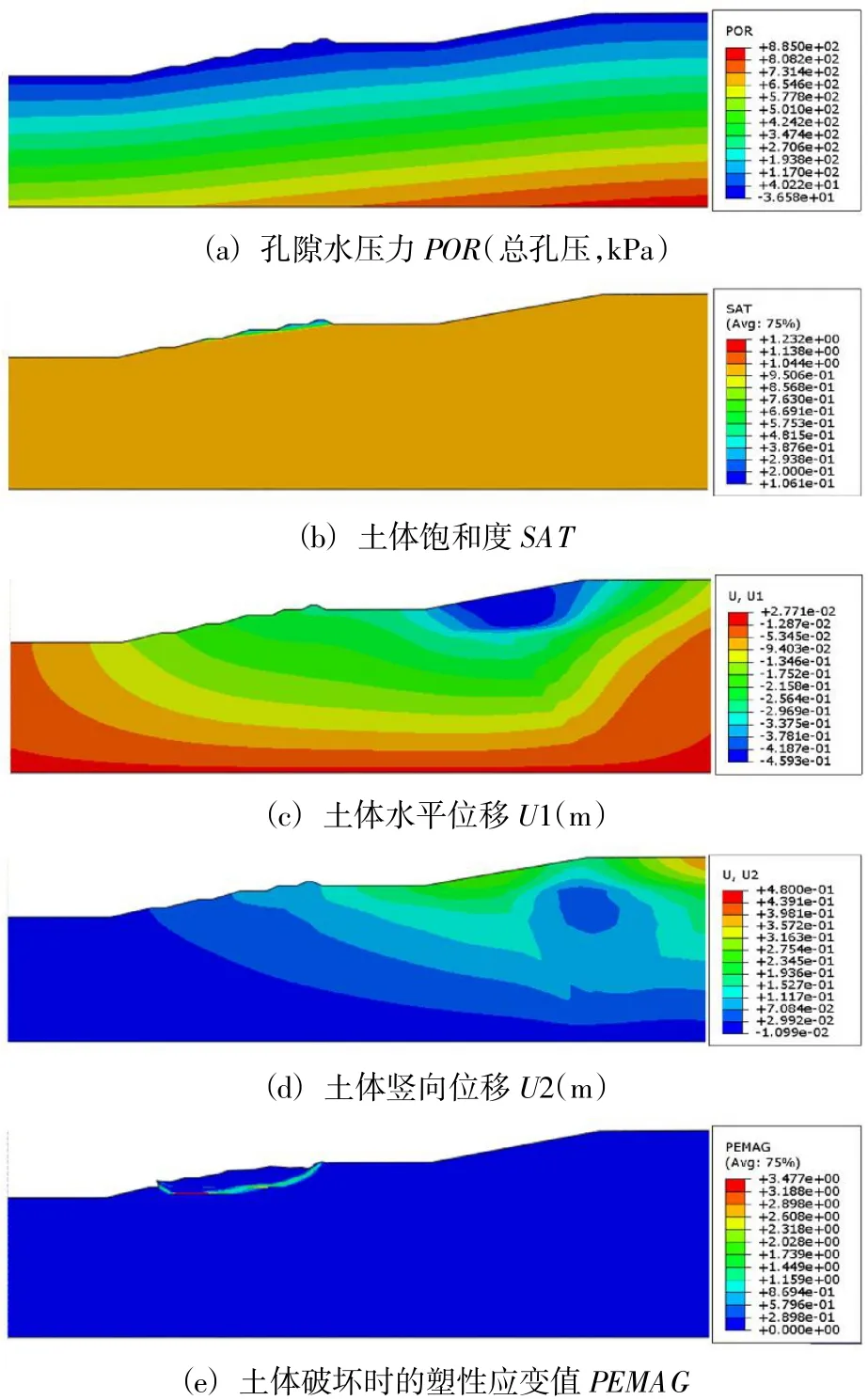
圖7 工況二邊坡響應(yīng)特征圖Fig.7 Response characteristic of slope of condition 2

4.3 計算結(jié)果討論

1）安全系數(shù)及位移

表2 為兩種計算工況下，邊坡穩(wěn)定安全系數(shù)，水平位移U1、豎向位移U2。從表中對比可以看出，隨著雨水入滲，邊坡穩(wěn)定安全系數(shù)由1.7 降至1.42，降低16.5%。水平位移由0.03 m 提高到0.25 m，大幅度增加可能的破裂寬度。需要指出的是，本文采用有效應(yīng)力法計算，得到的安全系數(shù)可直接用于指導工程設(shè)計，避免了總應(yīng)力法計算值偏低造成的設(shè)計過于保守。

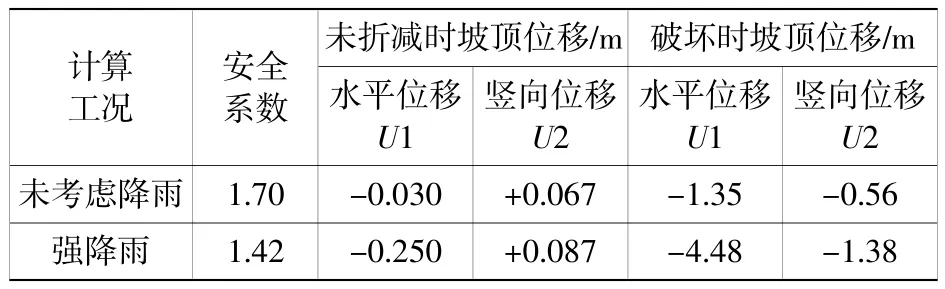
表2 不同工況下邊坡安全系數(shù)及坡頂位移Table 2 Slope safety factor and slope top displacement under different conditions

2）浸潤線

根據(jù)兩種工況對應(yīng)的邊坡孔壓（POR）、飽和度（SAT）分布圖（圖6～圖7）。由計算結(jié)果可以看出，在降雨入滲區(qū)域，孔壓會隨著降雨強度的增大而增大。同時，該部分區(qū)域的土體孔隙趨向于飽和，從而使得浸潤線往上移動。出現(xiàn)這種情況的原因是：土體滲透系數(shù)較小（0.512 4～3.24 mm/h），在強降雨（＞10 mm/h）入滲情況下，降雨強度遠大于土體滲透性，使得地表形成積水，降雨變現(xiàn)為“積水模型”或有壓入滲，入滲強度取決于土體滲透性，而不是降雨強度。

后期工程實際中經(jīng)歷了強降雨過程，并出現(xiàn)局部開裂現(xiàn)象，但未出現(xiàn)滑坡等整體穩(wěn)定問題，表明設(shè)計邊坡是合理的。研究成果為工程設(shè)計與實際施工提供了指導，也可為同類工程提供參考。

5 結(jié)語

本文基于更加真實反映土體特性的非飽和土體滲流方法，引入雨水入滲模型，分別計算了無降雨和強降雨情況下的孔隙水壓力、土體飽和度、邊坡位移、塑性應(yīng)變、安全系數(shù)等的影響，得到以下結(jié)論：

1） 無降雨情況下，邊坡強度安全系數(shù)為1.70；強降雨作用下，邊坡安全系數(shù)降至1.42，降低16.5%，忽略強降雨入滲影響的計算結(jié)果將偏于不安全。

2）強降雨工況較無降雨工況水平位移大大增加。兩種工況下，豎向位移都較小，且較為接近，表明雨水作用下，水平位移為主要變位。

3）在降雨入滲區(qū)域，孔壓會隨著降雨強度的增大而增大。同時，該部分區(qū)域的土體孔隙趨向于飽和，從而使得浸潤線往上移動。

4） 深基坑開挖過程中，特別是強降雨天氣下，建議在開挖交界面處設(shè)置防滲土工布等措施，進行防滲加固，減少雨水入滲影響。