XT260臥式冷室壓鑄機大杠再制造工藝路線優化研究

付 悅，楊 林，崔 晶

(沈陽工業大學 機械工程學院，遼寧 沈陽 110000)

0 前言

再制造工藝路線優化問題受到眾多學者的關注。如：江亞等以再制造能耗、成本、時間等多種因素為優化目標，以修復工藝與參數、資源配置等為約束前提，提出了一種基于遺傳-神經網絡的混合優化方法[1]。Li等建立了基于gert圖的再制造工藝路線模型，并就再制造生產計劃和控制策略等方面問題提出了基于混合細胞遺傳算法的再制造工藝優化方法[2]。基于此，本文以廢舊XT260臥式冷室壓鑄機大杠為研究對象，以失效特征為切入點，采用遺傳算法對其進行再制造工藝路線優化研究。

1 XT260臥式冷室壓鑄機大杠概況

壓鑄機大杠結構簡單,但其對設備剛性和穩定性有著很大的影響，長螺紋一端裝調模螺母連接尾板，短螺紋一端裝大杠螺母連接頭板。大杠在壓鑄成型過程中承受巨大的鎖模力，且在服役過程中不可避免受工況及外界因素等影響，容易出現磨損、腐蝕等失效形式而影響整機的壓鑄效果。由于大杠制造周期、加工成本及其本身的結構特點，通常對失效的大杠進行再制造修復后使用。由于廢舊大杠有很多不確定因素(如剩余壽命、失效特征等)，導致其再制造工藝路線多種多樣。修復工藝是再制造的關鍵環節，選擇合適的工藝路線并對其進行優化有利于提高生產效率、降低成本。

XT260臥式冷室壓鑄機大杠材料為42Cr，新件價格約為3 580元，主要參數信息如圖1所示。該大杠再制造工藝路線優化是對每一道工序選擇合適的機器與刀具，通過最佳設備組合達到成本與工時最小化的目標。

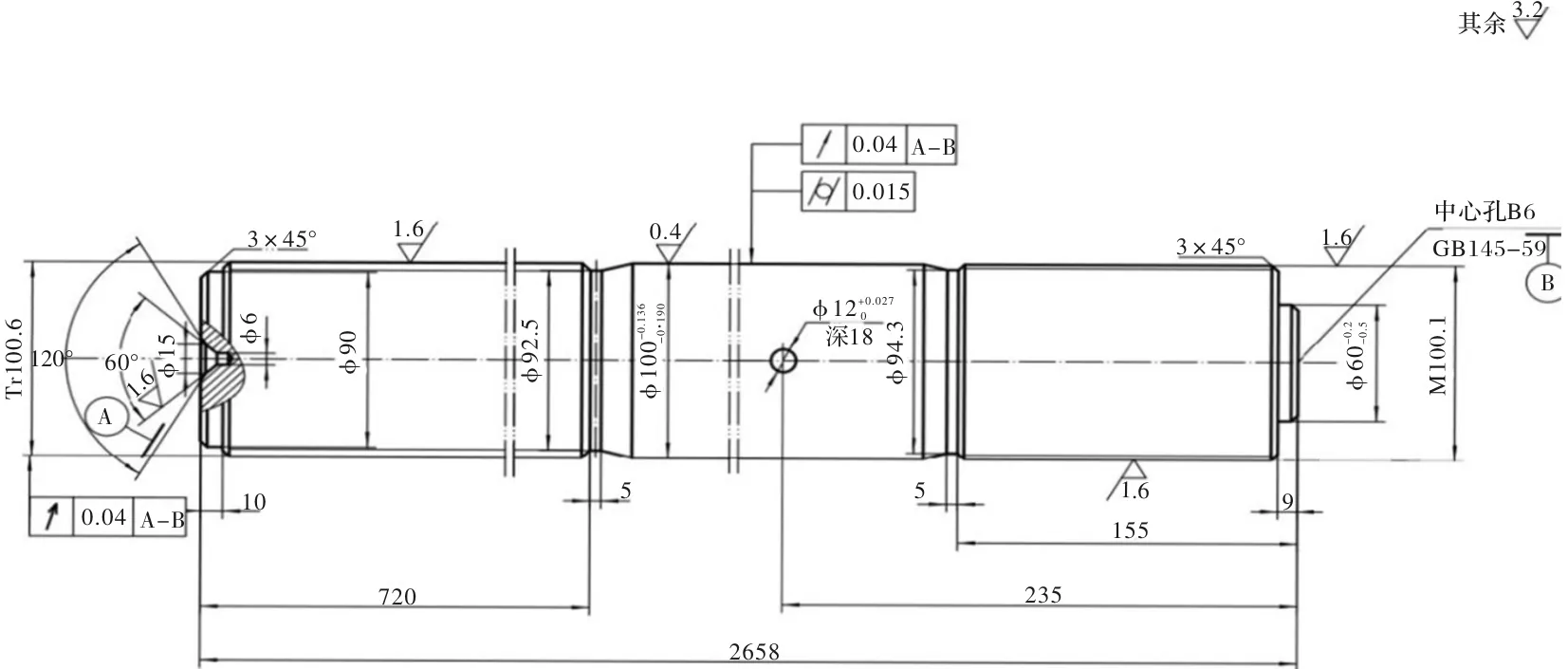
圖1 XT260臥式冷室壓鑄機大杠

2 失效特征分析

2.1 故障樹法提取失效特征

故障樹法是一種由上往下的演繹式失效分析法，并用專門的符號來表示上、下層次之間的聯系與制約[3]。廢舊XT260臥式冷室壓鑄機大杠故障樹的建立是從其表面狀況追溯到失效特征進而確定失效原因的過程。失效特征有利于選擇合適的修復工藝，為設計最佳修復方案提供依據。圖2為XT260臥式冷室壓鑄機大杠的故障樹模型，提取的失效特征為：P4、E1、E2、E3、E4、E5、E6，分別表示：變形、長螺紋磨損、表面損傷、短螺紋腐蝕、表面點蝕、長螺紋根部裂紋、局部疲勞裂紋。

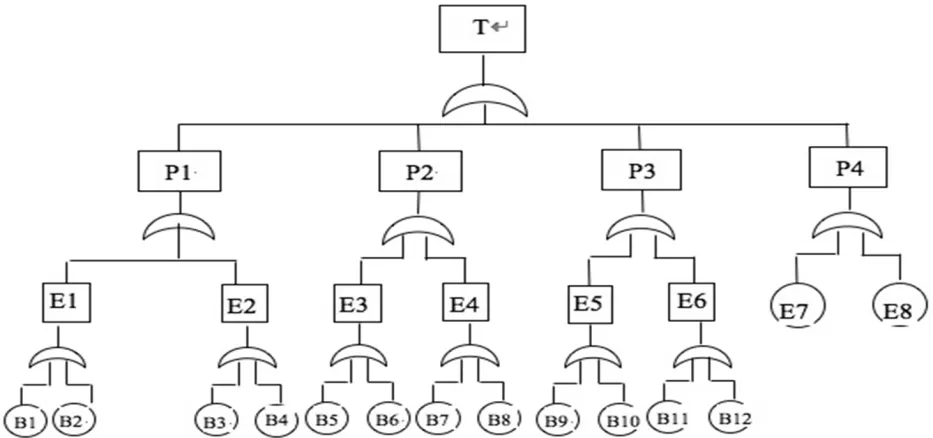
圖2 XT260臥式冷室壓鑄機大杠故障樹模型

2.2 損傷量模型獲取

損傷部位模型可通過圖3獲取，在此過程中，配準的兩模型對應點間的最大距離即為最大損傷深度，損傷深度決定鍍層厚度，影響修復工藝的選擇[4]。損傷深度將作為該大杠修復方案生成的主要參考依據。

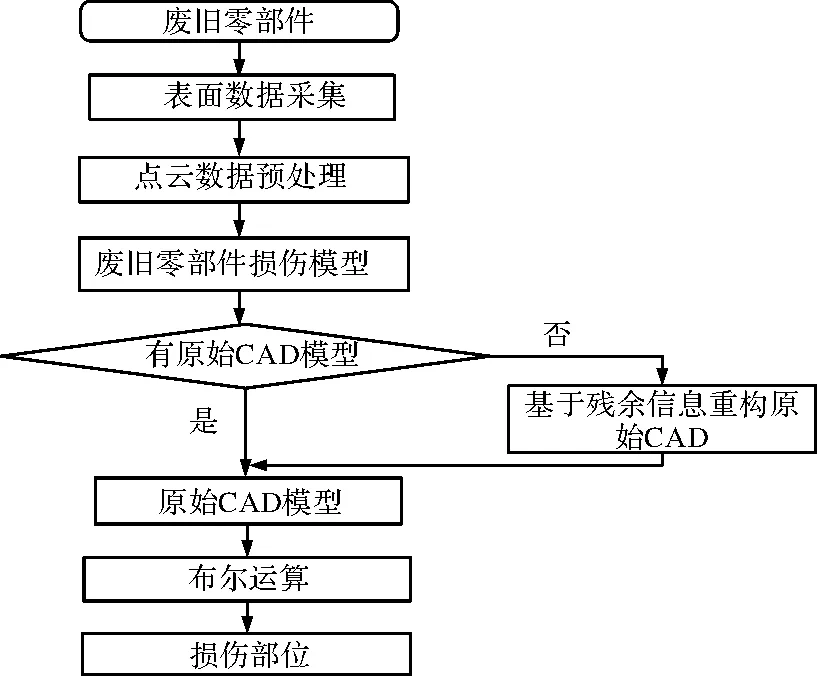
圖3 損傷量模型獲取流程圖

3 基于規則推理的再制造初始方案生成

針對廢舊零部件不同的失效形式、損傷程度等，一般會有與之相對應的修復工藝，且兩者存在一定的規則。采用規則推理的方法生成廢舊XT260臥式冷室壓鑄機大杠的再制造初始方案如表1所示，其表達形式為ifthen。

表1 大杠再制造修復方案

if失效部位=長螺紋表面

and失效特征=磨損

and磨損深度<0.5mm

then修復方案為：打磨,鍍鐵,車削,研磨,拋光

4 壓鑄機大杠再制造相關設備

壓鑄機大杠再制造過程中相關設備信息如表2和表3所示，刀具信息如表4所示。

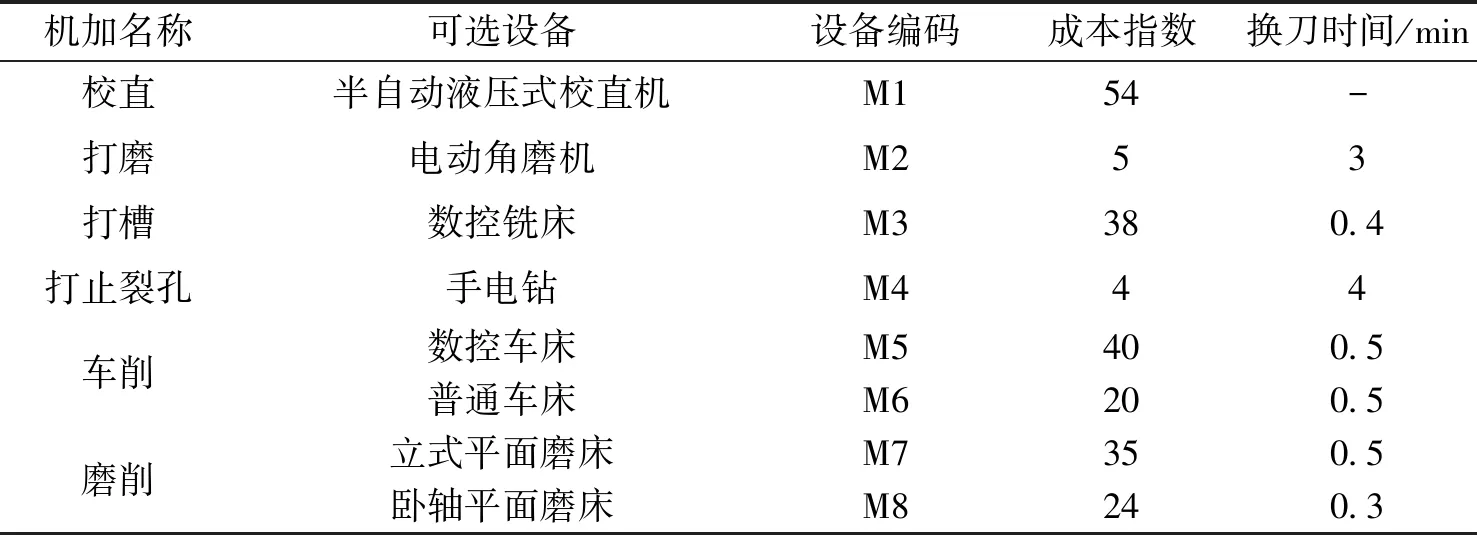
表2 機械加工設備信息

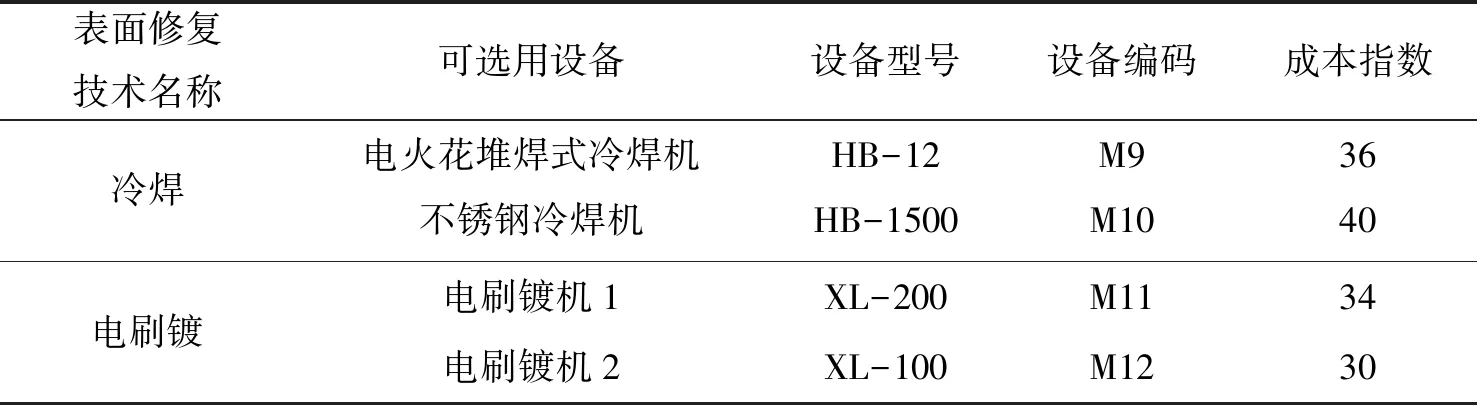
表3 表面修復設備信息

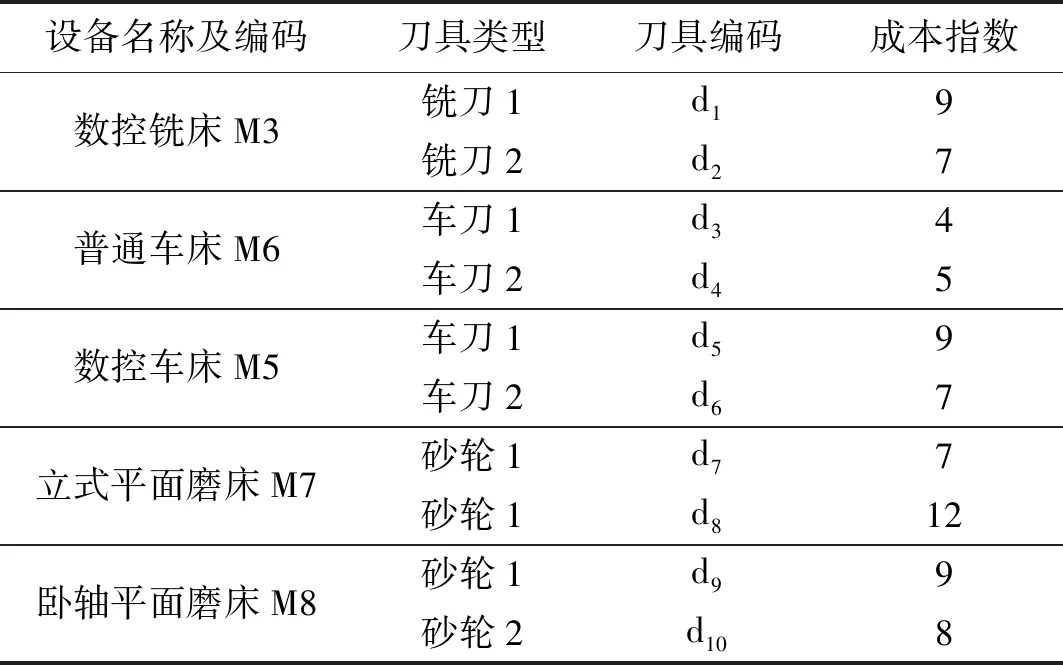
表4 刀具信息

5 基于遺傳算法的再制造工藝路線優化求解過程

5.1 約束描述

建立廢舊XT260臥式冷室壓鑄機大杠優化數學模型前，需要對其約束條件進行說明，具體如下：

(1)在優化過程中同一時刻該工件只能在一臺機器上加工且不發生中斷[5]。

(2)該工件各個失效特征間工序沒有先后約束關系，但一個具體失效特征的工序之間有先后約束關系。

(3)不同的失效特征具有相同的優先級。

5.2 構建目標函數

時間是再制造效率的直觀體現，費用直接關系到再制造產品的經濟性與企業效益。因此在構造大杠再制造優化目標函數時考慮時間和成本兩個因素[6]。

5.2.1 再制造時間函數

在不考慮裝夾、運輸等輔助時間的情況下，大杠的再制造時間函數可表示為表面工程技術加工時間(Tb)與機械加工時間(Tj)之和，即

(1)

式中，n為最大表面修復設備數量；ti為第i臺設備運用表面工程技術的加工時間。m為最大機加設備數量；tkq為第k臺機加設備切削時間；tkz為第k臺機加設備空載時間；tkh為第k臺機加設備換刀時間。

(2)

5.2.2 成本函數

大杠再制造時的成本主要考慮人工費(Cr)和設備費(Cs)，可表示為

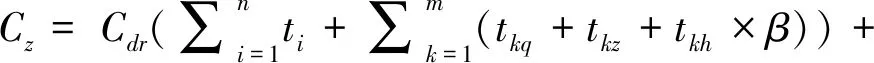
(3)

式中，Ck為第k臺設備在單位時間內的成本指數，對于具體規格的設備來說是個定值,Cdr為單位時間與人相關的成本指數，Cdr=30元/時。

5.2.3 目標函數轉化

在實際生產中成本與時間兩個目標函數往往存在沖突關系，且處理起來十分困難，不易求解。若將其先轉換為單目標優化問題再進行求解，會使得整個運算過程更加簡單直接，轉化后的數學模型可描述為

(4)

式中，w為權重系數，w1=0.35,w2=0.65，其數值通過層次分析法確定。

時間與成本兩個目標函數的量綱不同，在運算前統一規范成可以比較的形式。規范后的時間與成本目標函數可表示為

(5)

式中，Tmax、Cmax表示函數最大值，Tmin、Cmin表示函數最小值。

5.3 遺傳算法實現過程

(1)編碼。編碼的方法有很多種，但對于約束優化問題常用的是實數編碼法。實數編碼法無需特定的編碼與解碼過程，運算難度降低，執行效率提高，所以大杠再制造工藝路線優化采用實數編碼。

(2)適應度函數。大杠再制造工藝路線優化的目標函數總是非負的且是求最小值問題[7]，其適應度函數可表示為

(6)

(3)初始種群。一般群體規模在10～200之間，在運行該算法時將其設置為50。逐次以適應度值高的個體為模板并將不同的個體模板組成種群。若達到種群規模則進行下一步操作，否則在濾除的個體中選取適應度值大的來補缺[8]。

(5)交叉。根據再制造工藝路線優化特點，采用單點交叉操作，減少了不可行解的產生，使得算法效率顯著提高。交叉概率一般建議取值范圍是0.4～0.99，該算法中將其設置為0.6。

(6)變異。變異概率一般建議取值范圍是0.0001～0.1，該算法中將其設置為0.03，運行時根據該變異概率隨機的做某一規則的基因突變[10]。

(7)終止。算法迭代到500次時終止運行。

5.4 優化結果

根據初始信息、約束條件及設置參數等，通過matlab來運行該遺傳算法得到圖4。優化后的單目標函數值為72.54。其再制造成本為72.8元，時間為72.4 min ，最佳設備組合情況如表6所示。

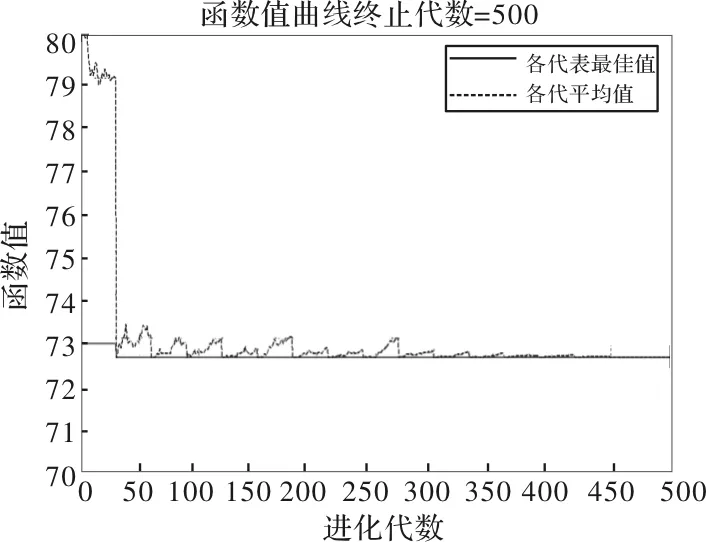
圖4 函數值與迭代次數關系圖

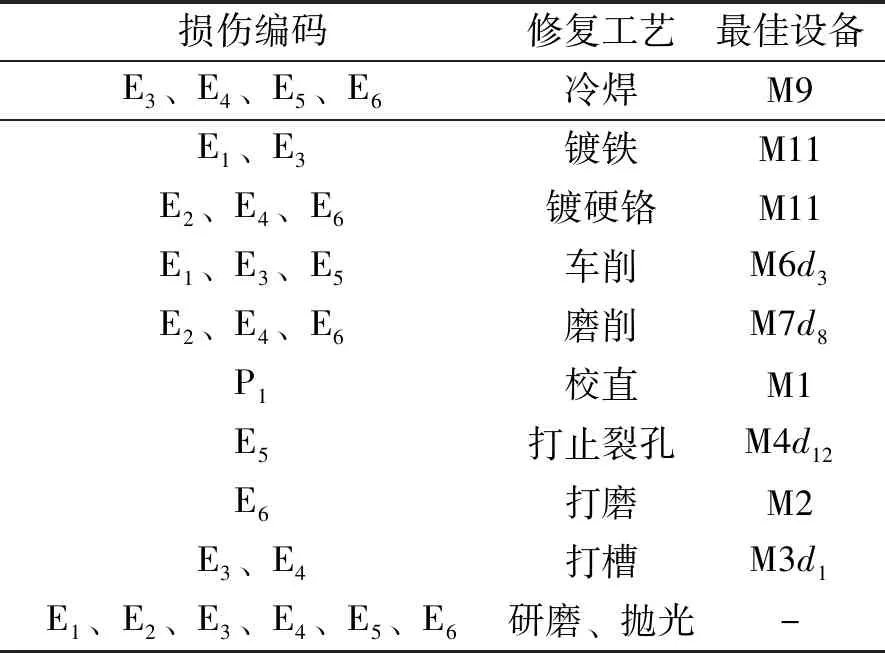
表6 最佳設備組合

6 結論

多數情況下大杠的再制造工藝路線仍由技術人員憑借經驗制定，具有強烈的主觀性缺乏科學性。因此采用遺傳算法對其進行優化研究，得到時間和成本最小化時的設備組合情況，可為車間實際生產提供些許參考。但再制造工藝路線優化是一個動態問題，在應用遺傳算法進行求解時，如何對算法中的重要步驟進行改善提高運算效率與準確度仍需進行深入研究。