多重不確定性需求下多產品訂單相似性研究

張青山， 劉巖峰，2， 徐 偉

(1. 沈陽工業大學 管理學院， 沈陽 110870； 2. 渤海大學 管理學院， 遼寧 錦州 121013)

用戶需求的不確定性，使得其對于裝備制造企業的產品需求也不相同。這種不確定性包括產品品種不確定、數量不確定、質量不確定、交貨期不確定等。由于客戶訂單的不確定性以及各種情況的發生，雖然客戶需求的產品品種不同，需求的時間、數量、質量以及交貨期等都不相同，但是這些訂單需求存在一定的相似性，如果能找到它們之間的相似性，就可以把相似性大的訂單進行并單處理或者組合處理。這樣就能有效地利用有限的資源滿足各種復雜的訂單需求，同時也可節省大量時間成本和生產成本。因此，研究不確定需求下訂單相似性十分必要，可以對出現相似性的訂單需求進行相似性智能處理，從而方便企業制定生產計劃或者修改、取消計劃，并制定出相應的訂單排產策略。

針對制造企業訂單相似性，很多學者和專家都進行了相應的工作和研究。韓文民等(2018)研究了緊急訂單下序位相似性問題[1]。張于賢等(2018)研究了多品種小批量的產品交貨期和加工工藝相似性訂單成組問題[2]。吳天行等(2017)基于巷道相似性和通道相似性研究了訂單分批問題[3-4]。陳俊等(2017)建立了產品質量屬性相似度模型和優化方法[5]。程賢福等(2017)研究了產品相似性等方面的適應性指標[6]。徐新勝等(2016)提出了解決產品結構相似性的判斷方法[7]。胡小林等(2019)研究了需求不均衡下揀選截止時間和通道的相似性[8]。禹春霞等(2019)為了滿足用戶需求，研究了用戶與候選服務商的相似性[9]。李若巖等(2019)采用模糊數學聚類法分析青海石腦油相似性[10]。施偉鋒等(2019)采用模糊C均值聚類算法分析屬性空間相似性[11]。王永泉等(2019)采用模糊聚類多層次分析法研究了零件間加工工藝相似性[12]。張青山等(2018)研究了雙渠道采購模式下裝備制造業選址生產問題[13]。韓世蓮(2016)研究了可以滿足多種客戶需求屬性的模糊系統聚類方法[14]。岳文軍(2015)采用RSCF分析法分析了訂單的相似性等特征對物流體系的影響[15]。

雖然很多學者對于產品或訂單相似性進行研究，但是沒有從需求的角度分析，研究在多重不確定需求的情況下訂單相似性問題。雖然有研究訂單的交貨期、工藝路線和數量，但是沒有將各種情況進行綜合研究。本文針對裝備制造企業多品種生產中基于多重不確定性需求的產品訂單相似性進行分析。

一、問題描述與分析

假設裝備制造企業共有N種產品，某段時間內有H個產品訂單需求，UncertainDemandh表示某一時刻的需求，包括需求到達的時間、需求的品種、需求的數量、需求的質量和需求的交貨日期等，具體可表示為UncertainDemandh=(DNh，DVh，DQh，DWh，DTh，PSh)。式中：h=1，2，…，H；DNh表示第h訂單需求到達的時間，其取值為0，1，2，…的非負整數，假設為隨機離散變量；DVh表示為第h訂單需求的產品品種，其取值為1，2，…，N，N+1的正整數，假設為隨機離散變量；DQh表示第h訂單需求的需求數量，其取值為正整數或者為批量的倍數，假設為隨機離散變量；DWh表示第h訂單需求的質量需求，假設為模糊區間需求；DTh表示訂單交貨期需求，假設交貨期需求為模糊區間需求；PSh表示訂單需求的情景，取值為：PSh=1表示正常訂單，PSh=2表示緊急訂單，PSh=3表示修改訂單。不確定需求的構成如表1所示。

表1 不確定需求的構成

二、具有多重不確定性需求的裝備制造企業多產品訂單相似性模型

對于產品的相似性.主要是考慮產品加工工藝的相似性。對于裝備制造企業來說，可以利用加工工藝的工序步驟來區分不同品種產品的相似性。對產品的細化，可以根據組件或者部件相似性來定義。產品相似性主要是由部件組成，包括組成部件的種類、部件的相似性、組件個數和產品組裝工藝。而產品組件的相似性由部件或組件的加工工藝、加工生產車間、加工時間等來定義。

1. 產品品種的相似性

設裝備制造企業的工件或組件有M個，Componentm表示第m個工件或組件。假設裝備制造企業共有Z個加工工序，則Processz表示第z個加工工序，并設ProcessNoz=z，z=1，2，…，Z，具體如表2所示。

表2 工序內容信息

設第m個工件或組件需要加工OPNumberm個工序，用OPm(g)表示第m個組件的第g個加工工序，則

OPm(g)=ProcessNoz(z=1，2，…，Z)

(1)

另外，設第m個工件或組件Componentm的加工工藝路線為Routingm，設其包括RoutingNumberm個工序，則

Routingm=OPm(1)→OPm(2)→ … →

OPm(OPNumberm)

(2)

則企業的工件或組件的內容信息構成如表3所示。

表3 工件或組件的內容信息

根據文獻[16]的工序相似性算法計算組件的相似性距離，記為Distance(m1，m2)，假設m1≠m2，表示工件或組件m2到工件或組件m1的加工工藝相似性距離。

計算工件或組件加工的步驟如下：

(1) 以m1組件為基準，對于其每一個工序i=1，2，…，RoutingNumberm1計算其在m2組件工序中的序號，用PosNumi(m1，m2)表示m1組件第i個工序OPm1(i)在m2組件工序Routingm2中的序號。如果m1組件的OPm1(i)在m2組件工序中則得到其序號，否則記為0。

(2) 對于步驟(1)中序號PosNumi(OPm1(i)，Routingm)之間的距離則有

(3)

其中：i=1，2，…，RoutingNumberm1-1

(3) 組件的相似性距離

RoutingNumberm1+1

(4)

則構建組件間相似性距離M×M方形矩陣，組件間相似性距離如表4所示。

由表4可知，以組件中距離最遠的組件與該行組件最不相似，距離最近的組件與該行組件最為相似。

表4 組件間相似性距離

假設similiar(i，j)表示組件組件i到j的相似性，則

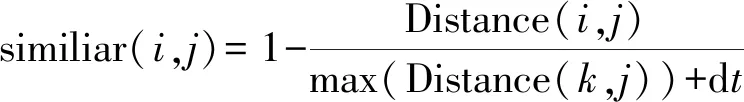
(5)

式中，dt是產品相似性偏移量。

本文采用取平均值最小的行所在的組件作為基準組件，以該組件為對比組件計算組件的相似性。假設取的平均值最小的行號為minLine，則組件相似性為similiar(minLine，j)，其中j=1，2，…，M。

2. 產品需求的聚類分析

首先，由于表1中多重不確定性需求的各項數據單位并不一致，所以需要進行歸一化處理，可以采用如下處理：

DNh取最低值為1，其他值為與該最低值的比值；DVh取最低值為1，其他值為與該最低值的比值；DQh取最低值為1，其他值為與該最低值的比值；DWh采用三角模糊進行處理，然后取模糊數最低值為1，其他值為與該最低值的比值；DTh采用梯形模糊進行處理，然后取模糊數最低值為1，其他值為與該最低值的比值；PSh以正常訂單為1，其他值為與該最低值的比值。

對UncertainDemandh進行歸一化處理。采用組件相似性為similiar(minLine，j)對產品種類DVh進行歸一化處理。到達時間DNh和交貨期DTh取最小的時間為1，其他值為與該最低值的比值。設歸一化后的矩陣UncertainDemand′={UncertainDemand′1，UncertainDemand′2，…，Uncertain-Demand′h}，其中UncertainDemand′h={DN′h，DV′h，DQ′h，DW′h，PS′h}表示第h=1，2，…，H個需求。

對于UncertainDemand′具有H個訂單需求，假設將這H個訂單需求分成type_num(2≤type_num≤H)個類別，則UncertainDemand′被分成{SK1，SK2，…，SKtype_num}的type_num個類別，U為相似分類值，并設各類別的聚類中心為{center1，center2，…，centertype_num}，設μhk為訂單需求Uncertain-Demand′h對于SKk的隸屬度，則可以將目標函數Jb表示為

(6)

dhk=d(UncertainDemand′h-centerk)=

(7)

式中：dhk表示第h個訂單需求UncertainDemand′h與SKk的歐幾里得距離；m為訂單需求的特征數；b為加權參數，其取值為1≤b≤∞。

為尋找一個最佳的分類，模糊C-均值聚類方法(FCM)要求該訂單需求對于類別的隸屬度值和為1，從而產生最小的函數值Jb，即滿足

(8)

利用式(5)、(6)來分別計算訂單需求Uncertain-Demand′h對于SKk的隸屬度μhk和type_num個聚類中心{centerk}，則有

(9)

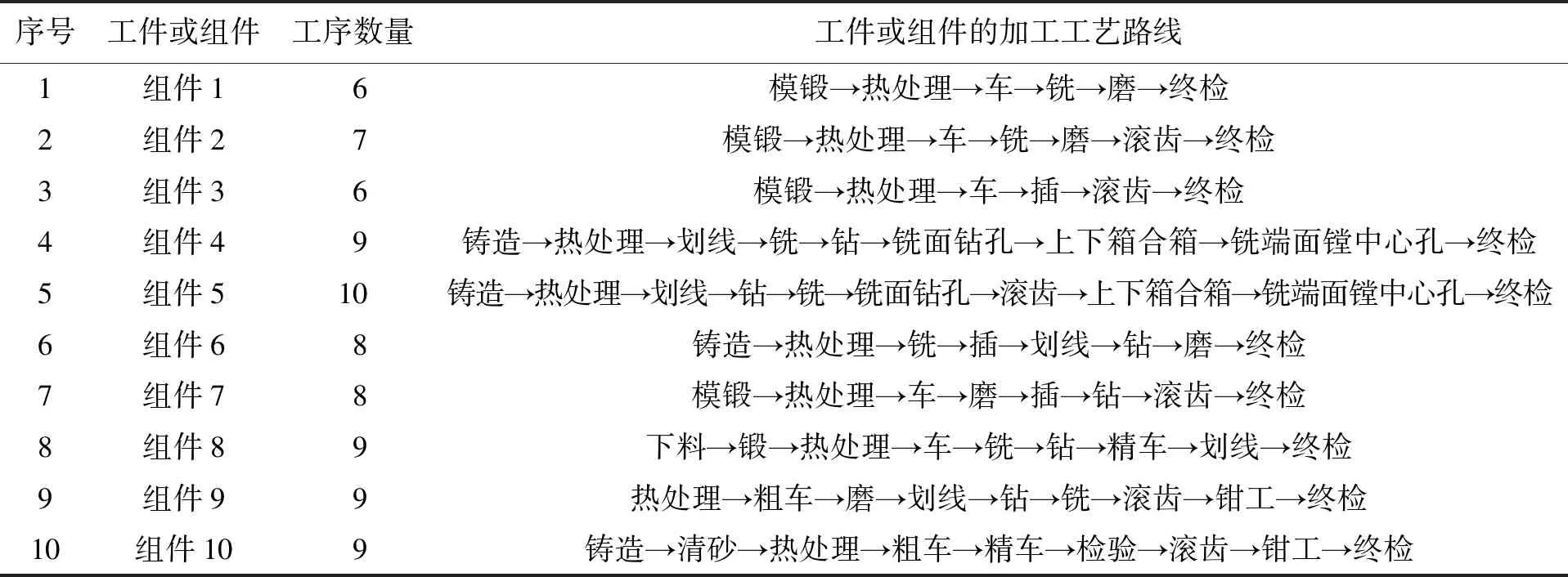
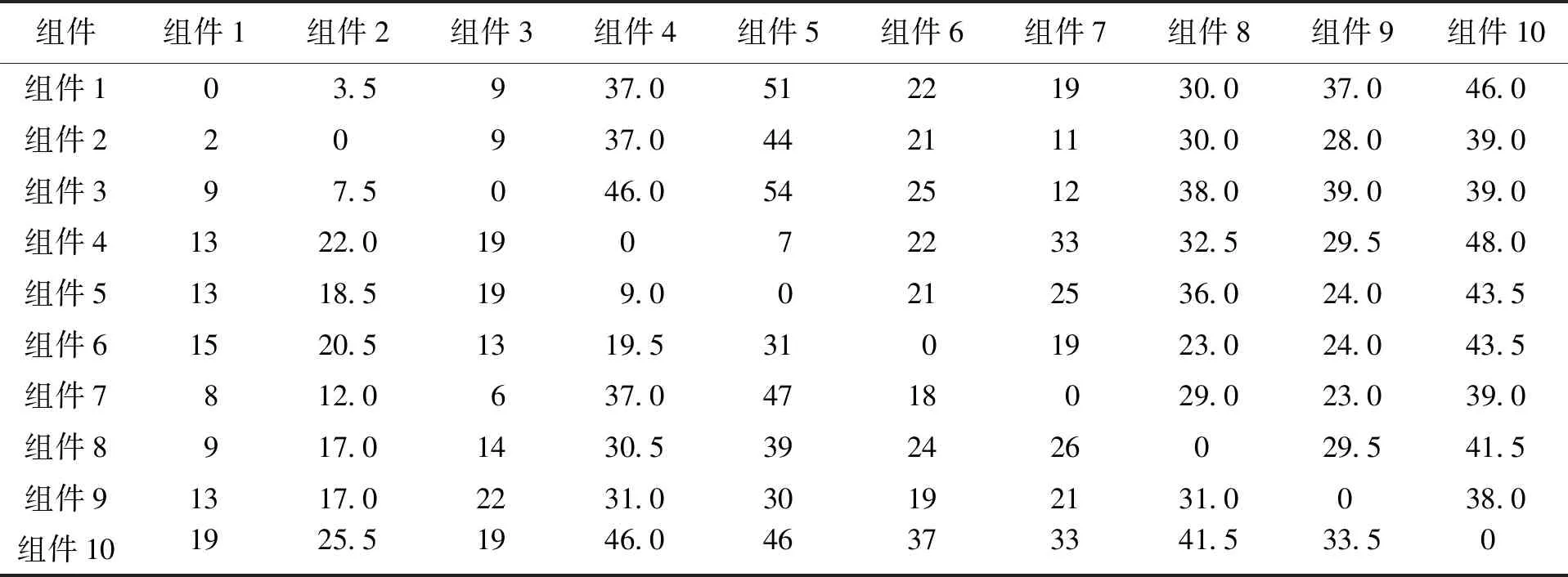
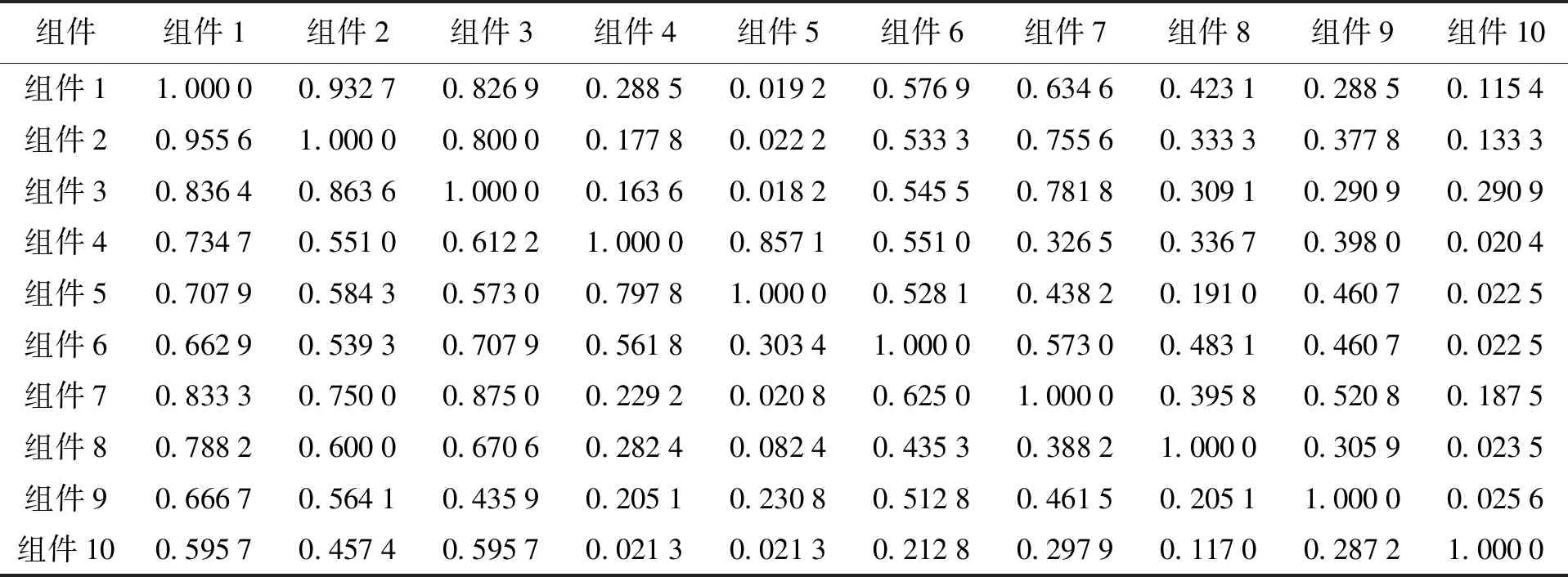
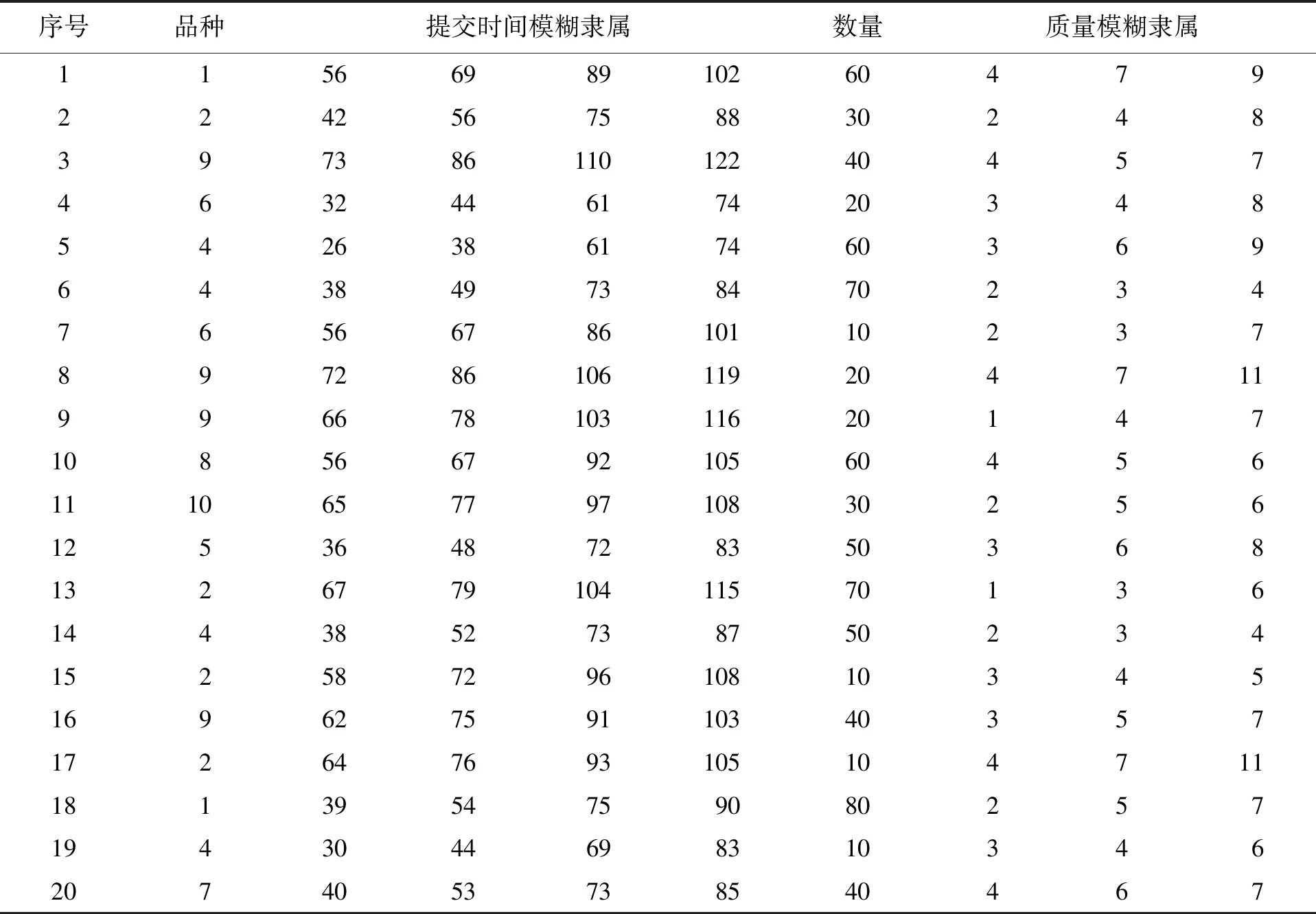
設Hk={h|2≤type_num

(10)

利用式(7)、(8)重復修改{center1，center2，…，centertype_num}、μhk和分類。當算法收斂時模糊聚類結束，從而獲得各類別的{center1，center2，…，centertype_num}以及μhk。

三、算例分析

假設某裝備制造企業工件或組件有10個，Componentm表示的是第m個工件或組件。假設裝備制造企業共有Z個加工工序，則Processz表示第z個加工工序，并設ProcessNoz=z，z=1，2，…，Z。設第m個工件或組件需要加工OPNumberm個工序，用OPm(g)表示第m個組件的第g個加工工序。工件或組件加工工藝如表5所示。

表5 工件或組件加工工藝

計算PosNumi(m1，m2)來表示m1組件第i個工序OPm1(i)在m2組件工序Routingm2中的序號，并以每個組件為基準計算每個組件的Pos-Numi(m1，m2)。表6為以m1=組件1為基準的每個組件的位置號，其他限于篇幅不一一列舉。

表6 以m1=組件1為基準的每個組件的位置號PosNumi(1，m2)

計算組件i到組件j的相似性距離，結果如表7所示。

計算組件i到j的相似性，其中產品相似性偏移量dt=1，結果如表8所示。

表7 組件間相似性距離

表8 組件間工藝相似性距離

將平均值最小的行所在的組件作為基準組件，即組件6，以其為對比組件計算組件的相似性。假設取平均值最小的行號為minLine=6，則組件相似性如表9所示。

假設某裝備制造企業的客戶需求如表10所示。進行歸一化處理，結果如表11所示。

表9 組件的工藝相似性

表10 某裝備制造企業的客戶需求

表11 某裝備制造企業的客戶需求歸一化處理

表11(續)

采用模糊C-均值聚類算法(FMC)對需求進行聚類。可以將20組需求按序號如下的方法進行聚類：第一類為2、8、9、11；第二類為1、5、6、10、13、18；第三類為3、12、14、16、20；第四類為4、7、15、17、19。

運行之后得到的目標函數值Jb=2.064 8，而且每次運行結果都不一樣。這跟初始聚類中的中心點有關系，其中某次聚類結果如圖1所示，三角形為各類的聚類中心點。

圖1 多產品訂單需求模糊C-均值聚類

四、結 語

本文根據產品組件的加工工藝過程進行相似性分析，找到相似性基準組件，并計算各組件之間的相似性。同時，針對訂單需求的多重不確定性，包括品種、數量、交貨期、質量等，采用模糊C-均值聚類算法對訂單需求進行聚類。采用算例對產品訂單需求的相似性進行分析，能夠解決現實中的訂單分組或成組生產問題。未來對相似訂單排產問題可以進行進一步研究。