基于離散元的貨艙內鐵精礦運動數值研究

李筱航，張建偉，吳文鋒，盧金樹

(浙江海洋大學船舶與海運學院，浙江舟山 316022)

國際海事組織于2011 年頒布了IMSBC 規則，其將固體散裝貨物分為A、B、C 三組，其中A 組為易流態化貨物。流態化是指散貨船在航行過程中遭遇海浪產生擺動與振動，貨物內部水分滲出，形成自由液面并發生運動，船舶復原力矩減小而穩性降低，導致事故發生。針對該類問題，周健等[1]采用PFC3D 對散裝鐵精礦流態化的宏觀情況進行了研究。SPANDONIDIS，et al[2]基于分子動力學方法對貨艙中固體顆粒的靜止角、材料屬性與運動特性間的聯系進行了研究。宋喜慶等[3]結合離散元與有限元方法，對顆粒運動特性進行了研究。李文頡等[4]通過靜傾斜實驗得出含水率和庫倫摩擦間的關系，并基于離散元法通過改變含水量，提出了船舶穩性數值評估方法。CHEN Wei，et al[5]建立了新的貨物臨界應力條件模型，為評估貨物穩定性提供了一種手段[5]。DE BLASIO[6]通過增大顆粒間作用力來模擬黏性力，在分子動力學基礎上建立了一套黏性物質顆粒的流動方法等。

目前，易流態貨物在貨艙內的運動規律研究日趨深入。為更清晰、直觀地展示艙內顆粒貨物運動情況及主要影響因素，基于離散元法，設計了共11 種計算工況，研究顆粒間摩擦系數、粒徑級配、顆粒碰撞恢復系數、貨艙橫搖幅值及裝載深度等因素對艙內鐵精礦顆粒運動的影響，以期為易流態貨物海上安全運輸提供參考。

1 數值模型建立

1.1 理論模型

根據牛頓第二定律，顆粒i 的運動方程如下：

式中：mi—顆粒i 的質量；Ii—顆粒i 的轉動慣量；—顆粒i 的加速度；—顆粒的角加速度；F—顆粒在質心處所受的合力；M—顆粒在質心處所受的合外力矩[7]。

顆粒間接觸模型采用Hertz-Mindlin (no slip)接觸模型[8]。其中，顆粒間接觸法向力Fn可由下式計算：

式中E*為等效彈性模量，R*為當量半徑，α 為接觸半徑。

利用中心差分法對式(1)進行數值積分，可得到兩次迭代時間中間點表示的更新速度為：

式中：Δt—時間步長；N—對應的時間t。

對式(3)進行積分，可得到如式(4)所示的位移等式：

將計算得到的位移帶入位移-力的關系中可以獲得新的作用，然后反復迭代計算，可獲取每一時刻顆粒受到的力和所處的位置。計算流程如圖1 所示，首先獲得初始接觸力Fi根據牛頓第二定律求出ui，然后根據位移和力的關系再得出Fi，繼而進行迭代計算。

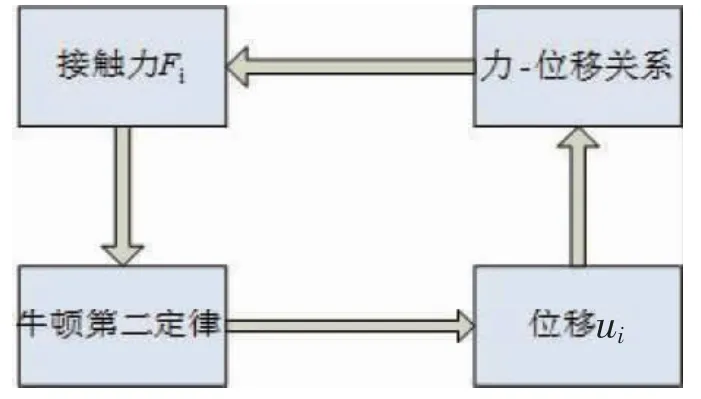
圖1 離散元方法流程圖Fig.1 Flow chart of discrete element method

1.2 模型驗證

基于文獻[1]進行本文數值模型驗證，仿真參數見表1。三維方箱做x 方向的簡諧往復運動，頻率1 Hz，振幅60 mm。仿真對比結果如圖2 所示，從顆粒整體運動表面輪廓可見，本文數值計算結果與文獻結果基本一致。可能的誤差在于：顆粒生成方式隨機，顆粒的初始狀態不能完全一致。

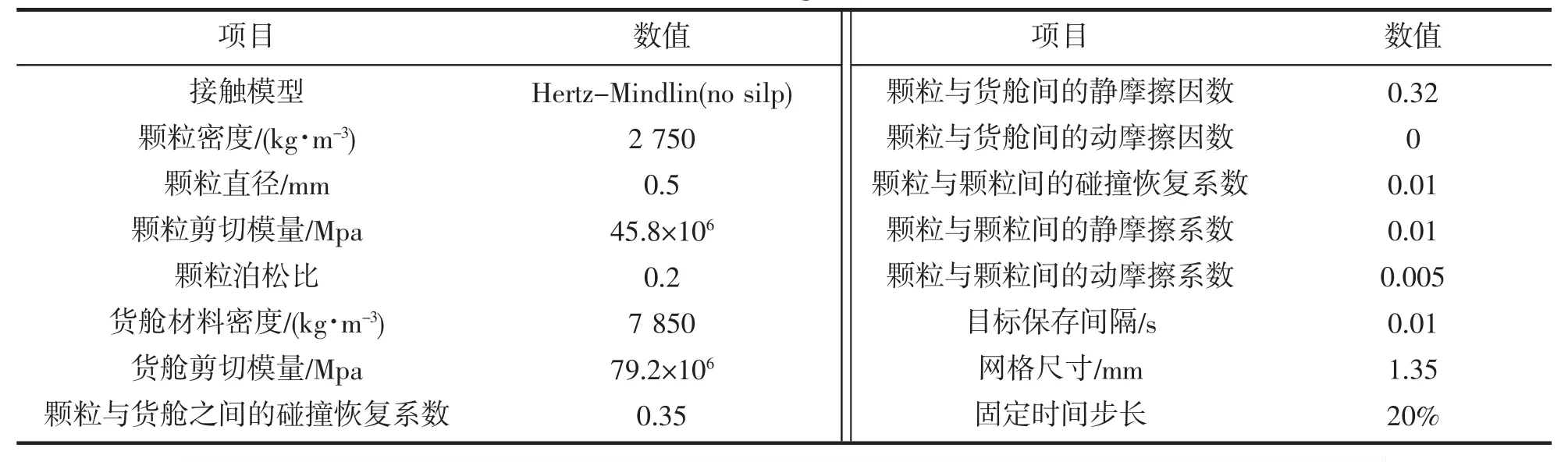
表1 模型驗證仿真參數設置Tab.1 Parameter settings of model validation

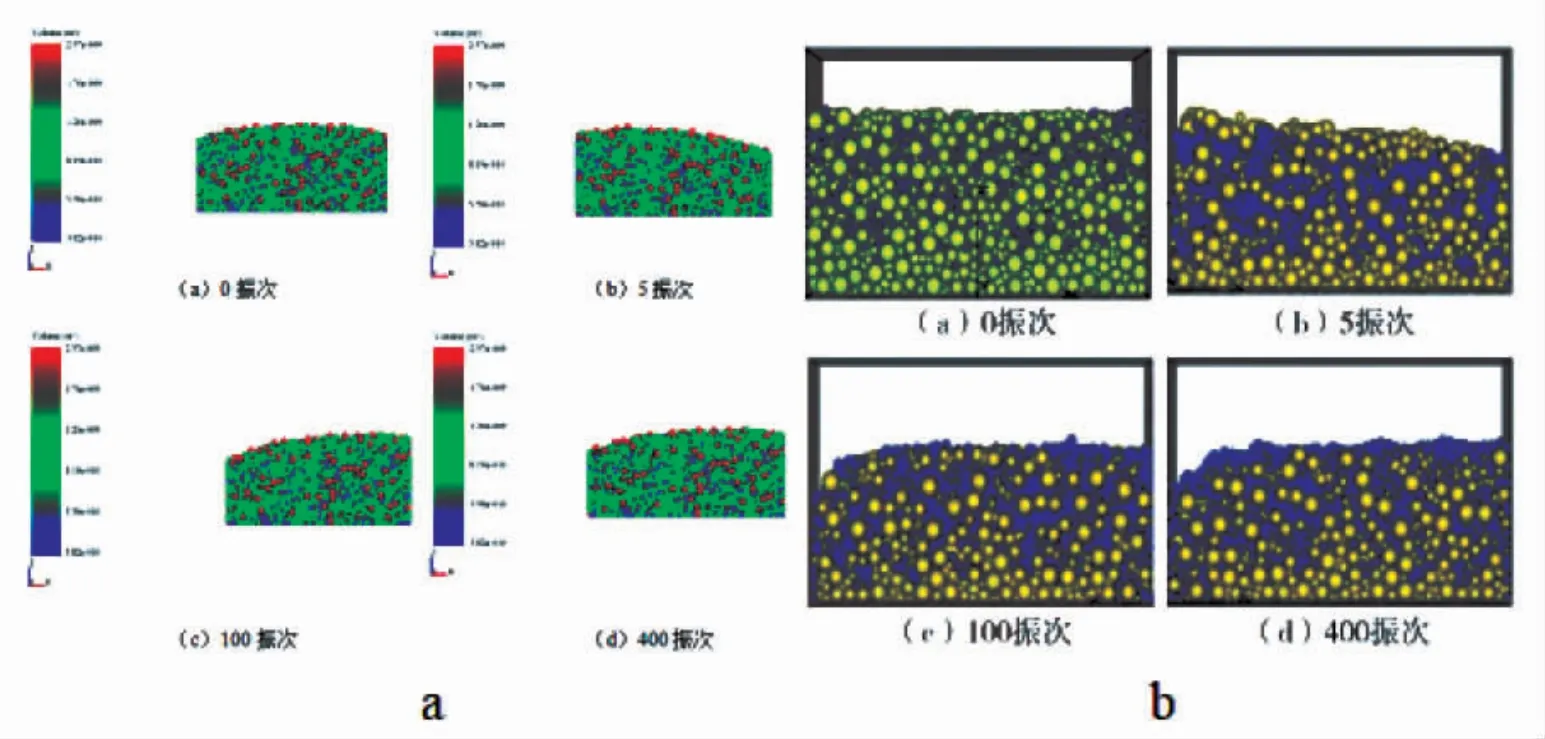
圖2 結果對比：(a)本文數值計算結果(b)文獻結果[1]Fig.2 Comparison of results：a：the present results b：results from reference[1]

2 研究方案

2.1 物理模型

以57 000 DWT 散貨船典型貨艙為原型[9]，考慮到數值模擬的局限性，考慮幾何縮尺比為1：660，實船貨艙及模型尺寸見表2 及圖3 所示。

表2 57 000 DWT 散貨船典型艙段及計算模型主尺度Tab.2 Typical sections of a 57 000 DWT bulk carrier and main dimensions of calculation model

貨艙模型如圖3 所示。

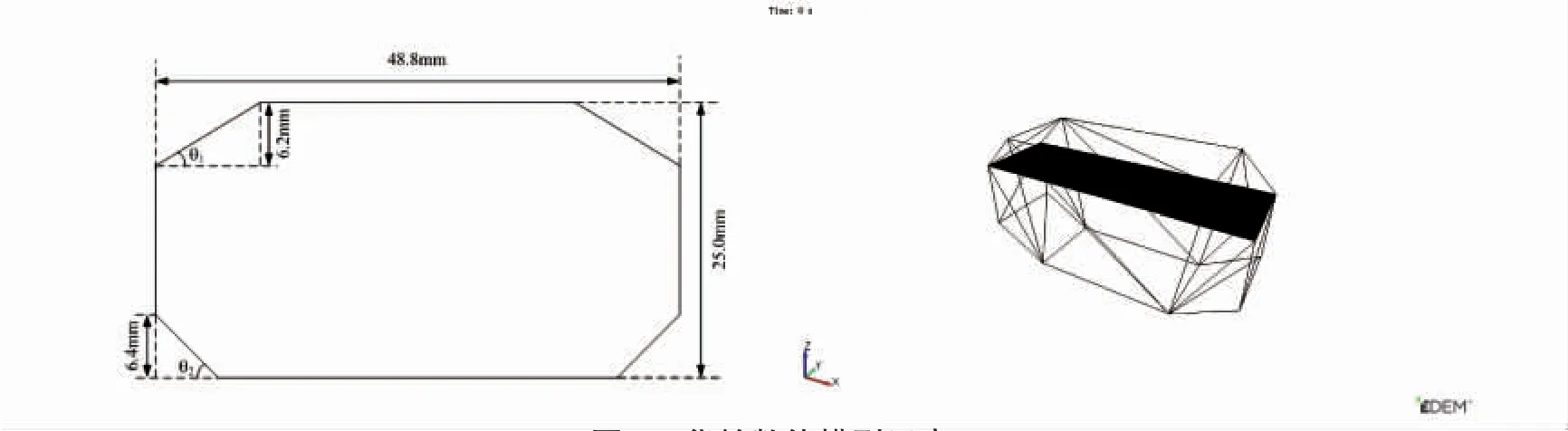
圖3 貨艙數值模型示意Fig.3 The cargo hold model

2.2 仿真工況

鐵精礦是我國主要的進口礦石貨種，也是易流態貨物海運事故高發貨種，與其他A 組貨物相比，其具有較高的比重，顆粒具有多層、微孔結構等特點[10]。鑒于數值模型驗證的可獲得性，研究選取鐵精礦作為研究對象，其顆粒屬性參數見表1。考慮到易流態化貨物的材料屬性及船舶在海上運輸的外部條件等因素，選取橫搖幅值、貨物裝載情況、摩擦系數、粒徑級配及顆粒碰撞恢復系數進行研究。具體參數如表3 所示。

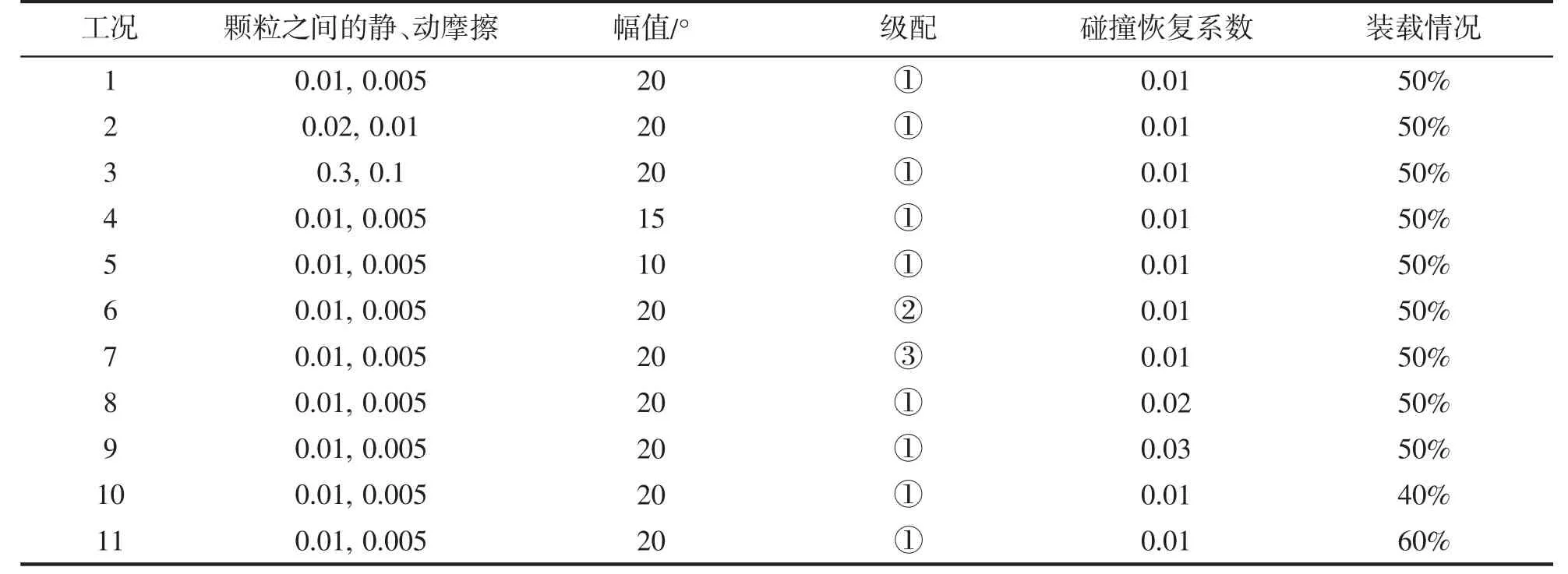
表3 計算條件設置Tab.3 Simulation conditions

利用User Defined 模塊配置粒徑級配，級配①為0.45 mm (10%)、0.6 mm (70%)、0.85 mm(20%)；級配②為0.45 mm (20%)、0.6 mm (60%)、0.85 mm (10%)；級配③為0.45 mm (10%)、0.6 mm (60%)、0.85 mm (30%)。運動形式為橫搖，由于實際運輸中顆粒運動比較緩慢，為加速顆粒運動，設定橫搖周期為1 s，搖擺中心為形心。時間步長20%，網格大小為顆粒的3 倍最小半徑，網格數為101 250 個。

3 結果分析

3.1 摩擦系數對鐵精礦顆粒運動的影響

不同摩擦系數下顆粒運動情況如圖4，可知工況1 顆粒傾斜程度最大，工況2 次之，工況3 顆粒傾斜程度最小，顆粒幾乎沒有流動。可見，顆粒庫倫摩擦系數越大，顆粒越不易發生流動。

圖4 9.75 s 時工況1(左)、2(中)、3(右)的顆粒分布情況Fig.4 Particle distribution of condition 1 (left),2 (middle) and 3 (right) at 9.75 s

顆粒法向接觸力為顆粒的法向沖擊力，其越大代表顆粒的碰撞次數越多、頻率越高、顆粒運動更劇烈，顆粒的動能是衡量顆粒運動速度的重要標志。特殊強調的一點是，當顆粒靜止不動時，也就是當時間為0時，在重力作用下，顆粒之間的法向接觸力為0.000 88 N。

工況1、2、3 顆粒法向接觸力、動能和重心偏移量對比如圖5 所示。可知摩擦系數越小，顆粒間的法向接觸力越大，顆粒的碰撞更劇烈，顆粒的法向接觸力隨著摩擦系數的增大而減少。摩擦系數改變后，顆粒的動能隨著摩擦系數的增大而減小。隨著摩擦力的增大，顆粒的重心偏移量變化越小，且在單個工況下，隨著時間的增加，在慣性的作用下顆粒難以返回初始位置，顆粒的行程會越來越大，導致貨物整體重心偏移量變大。

圖5 工況1、2、3 時法向接觸力(左)、顆粒動能(中)和重心偏移量(右)變化曲線Fig.5 Variation of normal contact force (left),particle kinetic energy (middle) and center of gravity deviation (right) under conditions 1,2 and 3

3.2 橫搖幅值對鐵精礦顆粒運動的影響

工況1、4、5 的仿真結果對比如圖6 所示，橫搖幅度越大，法向接觸力變化越明顯，峰值越大。三種工況隨著橫搖幅值的減小，顆粒動能遞減，貨物整體重心偏移量明顯減小。

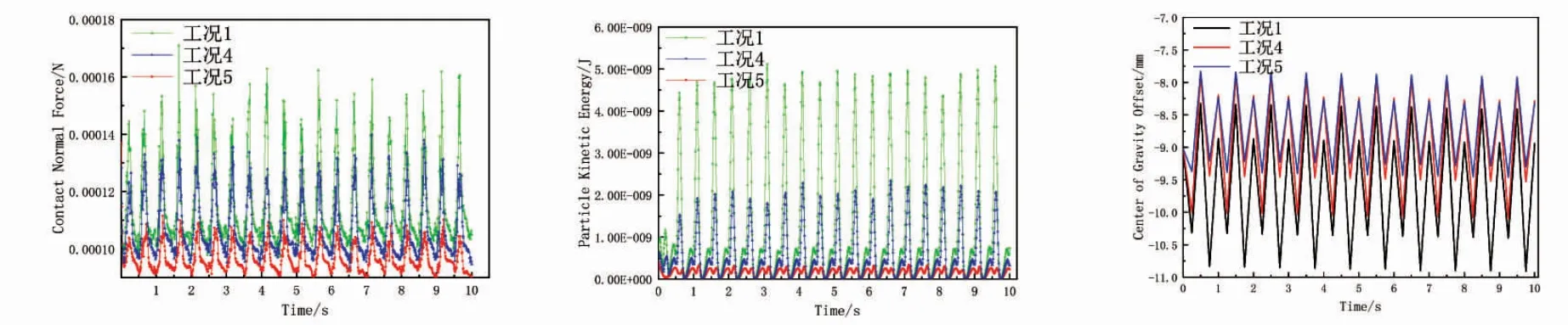
圖6 工況1、4、5 時法向接觸力(左)、顆粒動能(中)和重心偏移量(右)的變化曲線Fig.6 Variation of normal contact force (left),particle kinetic energy (middle) and center of gravity deviation (right) under conditions 1,4 and 5

3.3 粒徑級配對鐵精礦顆粒運動的影響

工況1、6、7 的數據對比如圖7。半載情況下，工況1、6 和7 分別裝載顆粒4 450 個、7 810 個和6 450個。從圖7 可以看出顆粒數量與顆粒碰撞程度成反比。工況6 與工況7 的動能峰值相差不大，工況6 的顆粒動能峰值略大，工況1 的顆粒動能峰值遠遠高于其他兩個工況。裝載深度相同的情況下，顆粒越多重心越高，但重心偏移量相差不明顯。

圖7 工況1、6、7 下法向接觸力(左)、顆粒動能(中)和重心偏移量(右)的變化曲線Fig.7 Variation of normal contact force (left),particle kinetic energy (middle) and center of gravity deviation (right) under conditions 1,6 and 7

3.4 碰撞恢復系數對鐵精礦顆粒運動的影響

工況1、8、9 的數據對比如圖8，可知顆粒法向接觸力幾乎沒有差別，并且3 種工況下的顆粒動能變化曲線完全一樣。由此可見，不同的碰撞恢復系數對顆粒的法向接觸力和動能并沒有較大影響。3 種工況的重心偏移量也基本相同。

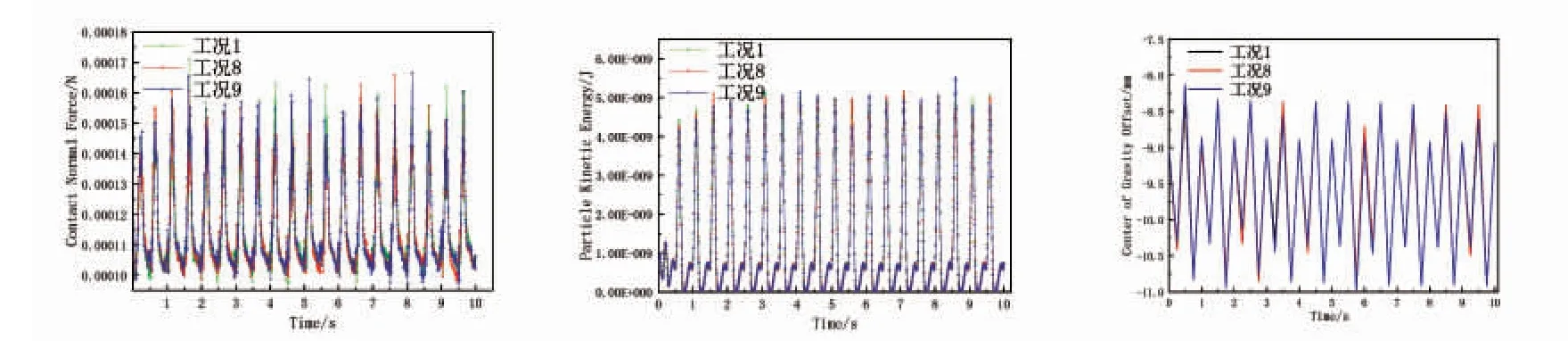
圖8 工況1、8、9 時法向接觸力(左)、顆粒動能(中)和重心偏移量(右)的變化曲線Fig.8 Variation of normal contact force (left),particle kinetic energy (middle) and center of gravity deviation (right) under conditions 1,8 and 9

3.5 貨物裝載情況對鐵精礦顆粒運動的影響

工況1、10、11 的數據對比如圖9，可知貨物裝載量與顆粒的碰撞程度成正比，工況1 和工況10 的法向接觸力峰值基本相同，但工況1 的法向接觸力變化幅度大，說明工況10 在高裝載率下顆粒碰撞較為劇烈。工況1 和工況10 的顆粒動能幾乎一樣，工況1 的顆粒動能維持在一個較低的水平。工況11 顆粒的重心偏移量變化幅度更大，工況10 的重心偏移量變化幅度最小。

圖9 工況1、10、11 法向接觸力(左)、顆粒動能(中)和重心偏移量(右)的變化曲線Fig.9 Variation of normal contact force (left),particle kinetic energy (middle) and center of gravity deviation (right) under working conditions 1,10 and 11

4 結論

本文通過與其他文獻結果進行對比驗證了模型的正確性，確定了11 種工況，對散貨船貨艙內的鐵礦石顆粒在不同工況下的運動情況進行了數值模擬，通過改變摩擦系數來代替不同含水量的影響，得出以下結論：

(1)本研究通過改變顆粒間摩擦系數來替代含水量的影響具備正確性和可行性，本文構建的鐵精礦顆粒艙內運動數值仿真模型能夠正確處理顆粒材料在艙內的運動仿真。

(2)顆粒摩擦系數增加即貨物含水量增加，則顆粒運動幅度明顯降低；單個工況下，由于慣性的作用，顆粒的運動幅度隨時間的延長不斷增加。橫搖幅值的增加會導致顆粒碰撞更加劇烈，顆粒的重心偏移量變化幅度會更大；碰撞恢復系數的改變對顆粒的運動情況幾乎沒有影響；在裝載體積一定的情況下，顆粒越少的粒徑級配，顆粒的運動幅度越大；隨著顆粒裝載的增多，顆粒的法向接觸力和動能會維持在一個更高的水平。