基于自適應參數調節和動態分組學習的水波優化算法*

林偉豪，何杰光，肖佳嘉

(廣東石油化工學院 計算機學院，廣東 茂名 525000)

鄭宇軍提出基于淺水波理論[1,2]的水波優化算法(WWO)，該算法模擬水波運動中存在的傳播、反射、碎浪等運動，且在旅行商問題和車輛路徑[3]問題得到了較好的應用。張蓓等[4]分析了WWO執行傳播和折射操作時的收斂情況，并驗證了上述兩種情況的收斂條件。杜兆宏等[5]提出自適應碎浪系數調整策略來平衡算法的全局勘探和局部開發能力。顧啟元等[6]采用雙種群進化結構維持種群多樣性并提高個體學習效率。綜上，可以看出WWO在收斂速度和收斂精度上仍具有較大的改進空間，基于此本文提出了基于自適應參數調節和動態分組學習的水波優化算法(DGLWWO)。DGLWWO以非線性變化的碎浪系數來平衡算法的搜索機制，并設計了基于正余弦因子的動態分組學習階段，主群與子群的信息交流機制使算法在進化后期仍有找到最優解的可能。

1 原始水波優化算法

1.1 傳播

(1)

λ=λ·α-(f(X)-fmin+ε)/(fmax-fmin+ε)

(2)

式中：α為波長衰減系數；fmin和fmax分別為最優和最差的水波；ε為一個很小的正數。

1.2 折射

當水波波高h遞減為零時，按式(3)執行折射操作，并將波長重置為h=hmax。

(3)

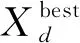
1.3 碎浪

(4)

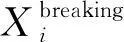
2 基于自適應參數調節和動態分組學習的水波優化算法

2.1 碎浪系數β的自適應調節

碎浪系數β控制在最優水波附近密集搜索孤立波的范圍，β越大，搜索范圍越大，全局搜索能力越強。WWO的β隨迭代次數的增加而線性遞減，無法很好地平衡算法前期的全局搜索能力和后期的局部開發能力。基于此，本文設計了正弦變化的碎浪系數β，其表示為

(5)

圖1 自適應碎浪系數

WWO和DGLWWO的碎浪系數如圖 1所示，DGLWWO在進化前期保持較大的碎浪系數，有利于支持算法的全局搜索，特別是在求解多局部最優值問題時，一定程度上提高了找到其他更優解的概率。而隨著迭代的進行，碎浪系數迅速減小，使算法能夠進行更多的局部精細開發。

2.2 基于正余弦因子的動態分組學習階段

為了解決WWO種群后期進化緩慢的問題，本文設計了基于正余弦因子的動態分組學習階段。其動態分組策略過程主要是，隨機從[2,10]內選擇分組規模M，分成Np/M個分組，當Np%M≠0時，最后一個分組規模為M+Np%M。動態分組學習階段可表示為

(6)

(7)

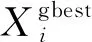
式(6)中，水波以正弦方式向組內最優個體靠近，在全局范圍內搜索，并維持種群多樣性。式(7)中，水波以余弦方式向全局最優個體靠近，進行局部開發，加快算法收斂。正弦全局搜索能夠有效彌補余弦局部開發而導致陷入局部最優的缺陷，而余弦局部開發提高了算法的尋優性能。由此可知，動態分組學習促進了個體之間的信息交流，這在避免算法早熟、提高收斂精度的同時，提高了算法的求解效率。

2.3 DGLWWO實現流程

DGLWWO的執行步驟如下：

(1)隨機生成一個規模為Np的種群，并計算每個水波的適應度值，找到最優水波；

(2)按式(1)～(5)，對每個水波執行傳播、折射、碎浪操作；

(3)動態分組，隨機選擇分組規模M，生成Np/M個分組；

(4) 按式(6)、式(7)，執行動態分組學習階段；

(5)更新每個水波的波長，并計算每個水波的適應度值，求得全局最優解；

(6)若滿足結束條件，則輸出全局最優解；否則，執行(2)。

3 仿真實驗與分析

3.1 測試函數及參數設置

為驗證DGLWWO的有效性和穩定性，選取10個標準測試函數進行測試，并與原始WWO算法[1]、LOGWWO算法[5]、ACLWWO算法[6]、S-WOA算法[7]進行對比。測試函數及其特性，結果見表1。所有算法的最大迭代次數設置為1000，每個算法獨立運行20次，問題求解空間的大小D為30。WWO、LOGWWO、S-WOA、DGLWWO的種群規模均為10，WWO、LOGWWO、DGLWWO的波長λ=0.5、波高hmax=12、碎浪系數的最大值和最小值分別為βmax=0.250和βmin=0.001、波長衰減系數α=1.0026；ACLWWO的參數來源于文獻[6]，主種群和子種群規模均為20，子種群波高為hmax=100，波長衰減系數α=1.0260。

表1 標準測試函數

3.2 基于正余弦因子的動態分組學習階段有效性驗證

為了驗證基于正余弦因子的動態分組學習階段的有效性，構造4種不同的算法進行對比性實驗，分別是DGLWWO、DGLWWO-DGL(不使用動態分組階段)、WWO和WWO+DGL(加入動態分組學習階段)。選用f5作為測試函數，f5是一種極難搜索全局最優解的病態非凸單峰函數，適合用于測試算法的收斂性。4種算法分別在f5上獨立運行20次，結果如表2所示，平均收斂曲線如圖2所示。

表2 4種算法分別在f5上的收斂性

a 動態分組學習階段的收斂過程 b 動態分組過程的穩定性

由表2可知，DGLWWO和WWO+DGL表現出更好的收斂精度，這說明動態分組學習階段有利于增強種群多樣性，提高算法的尋優能力。由圖2可以看出，DGLWWO和WWO+DGL的收斂速度明顯優于DGLWWO-DGL和WWO，雖然4種算法都較早地陷入了局部最優，但對比WWO和WWO+DGL的穩定性可知，動態分組學習階段在提高收斂精度和收斂速度的同時，能夠有效保證算法的穩定性。綜上所述，動態分組學習階段有效地避免了算法過早丟失多樣性，提高了算法的收斂精度和收斂速度。

3.3 實驗結果及分析

各算法的平均收斂曲線如圖3所示，收斂結果如表3所示。

圖3 算法平均收斂曲線情況

表3 各算法收斂結果

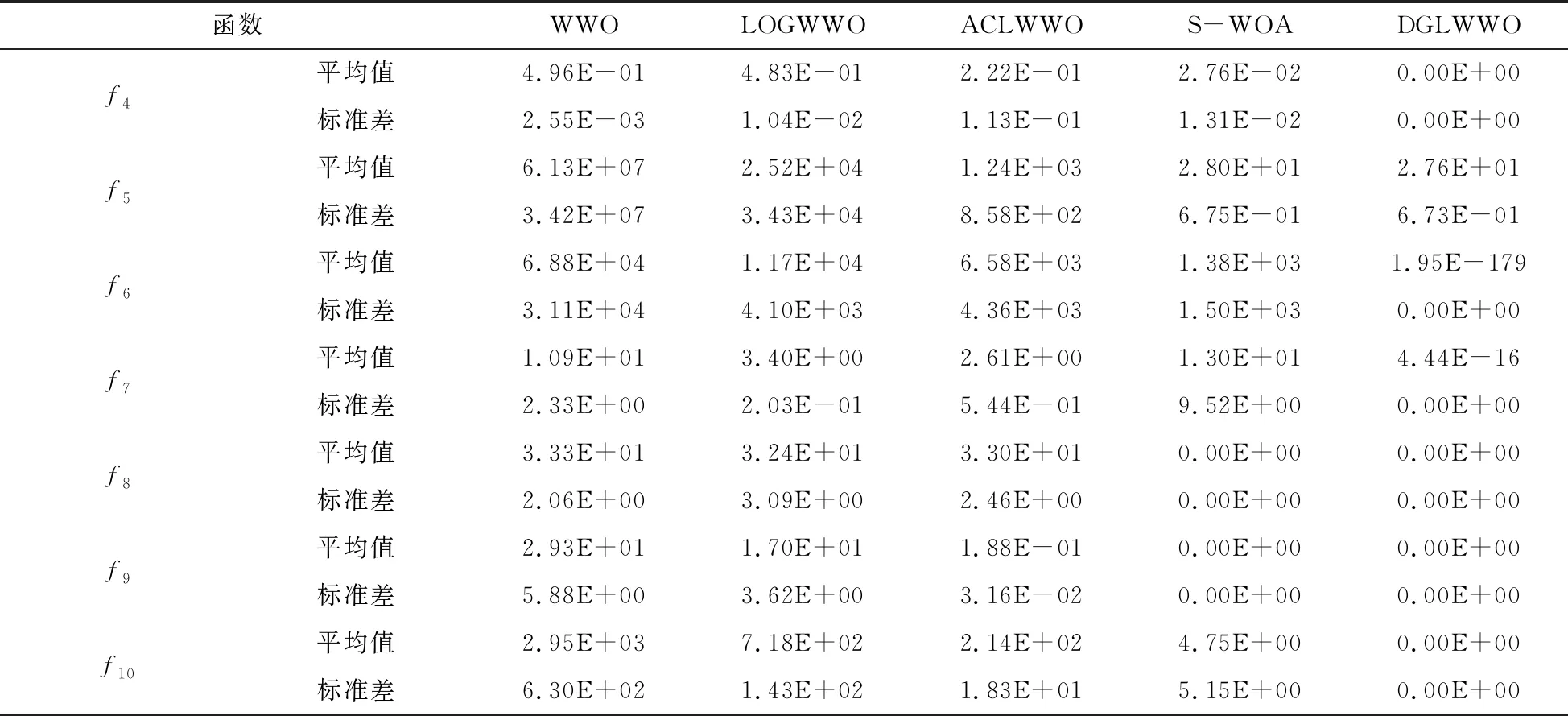
續表

由圖3可知，函數f1～f6的收斂速度明顯優于其他算法，函數f1～f3迭代200次就已尋得理論最優解；函數f4求解時能迅速收斂并找到最優解；與其他算法相比，函數f5和f7在小于200次迭代時就已尋得較好的精度，但隨之出現了進化停止的現象；函數f6在小于400次迭代時收斂速度較快，在進化后期仍能表現出較好的尋優能力，能夠進一步提升收斂精度；函數f8～f10在小于50次迭代就已求得最優解，說明DGLWWO在求解復雜問題時更具優勢。

由表3可知，DGLWWO的收斂精度均優于其他算法，其中對函數f1～f4均能求得其理論最優解；函數f5～f7雖然沒有求得最優值，但其求解精度分別至少提升了2個、176個和15個數量級，并且獲得了最小的標準差；對復雜多峰函數f8～f10均求得理論最優解。這說明，DGLWWO在收斂精度和穩定性方面表現出較好的競爭性。

綜上，基于正余弦因子的動態分組學習階段使DGLWWO在進化后期仍能保持較好的種群多樣性，仍具有找到更優解的可能，有效地協調了算法進化前期的全局探測能力和后期的局部開發能力。此外，碎浪系數的自適應調節對于提高DGLWWO的優化性能提供了一定的幫助。

4 結語

本文針對WWO存在的缺陷，提出了基于自適應參數調節和動態分組學習的水波優化算法DGLWWO。DGLWWO設計了基于正余弦因子的動態分組學習階段，主群與子群的信息交流機制和動態變化的分組策略，有效地避免了種群過早丟失多樣性，同時提高了算法后期仍能進化的概率。實驗表明，DGLWWO保持了WWO的優點，同時極大地提高了WWO的優化性能。