陶瓷/鈦合金靶抗圓柱體彈侵徹的仿真研究

張元豪,程忠慶,侯海量

(1.海軍工程大學 艦船與海洋學院,湖北 武漢 430033;2.海軍勤務學院,天津 300450)

全世界范圍內反艦導彈正不斷發展,半穿甲反艦導彈侵入船體內部爆炸,產生的高速破片會對艦船重要艙室及人員造成嚴重影響,所以艦船艙壁的抗穿甲問題引起了廣泛的關注。為提高艦船的生命力,艦船裝甲從單一的均質金屬裝甲逐步發展為復合裝甲。

陶瓷裝甲具有低密度、高硬度、高抗壓強度等特點,適合用作復合裝甲的迎彈面板,國外針對將陶瓷作為艦艇、坦克等大型戰斗設施的主體防彈材料已有大量的研究[1-3]。但是陶瓷由于自身的塑性差、斷裂強度低,不能單獨用作防護裝甲,因此需要背板剛性支撐。目前采用的陶瓷復合裝甲一般采用金屬材料作為背板,陶瓷面板用于碎裂鈍化破片[4-5],金屬背板用于吸收破片動能。

張曉晴[6]通過彈體撞擊陶瓷/金屬復合靶板實驗及理論分析模型,得到了侵徹動態過程及相關規律。王曉強等[7]通過實驗研究了10 g破片模擬彈侵徹不同厚度配比的陶瓷/船用鋼靶板的彈道極限速度,得到了彈道極限速度隨陶瓷厚度和船用鋼厚度變化的經驗公式。遲潤強等[8]利用有限元軟件對氧化鋁陶瓷/鋁合金復合裝甲的防護性能與彈靶尺寸的關系進行了研究,建立了彈道極限速度的經驗公式。孫杭其[9]討論了陶瓷/鋁合金復合裝甲的優化設計問題,對其厚度配比進行優化。匡格平[10]則采用數值模擬方法研究了陶瓷/鈦合金結構下,彈靶尺寸對剩余速度的影響以及彈丸初速度對侵深的影響,得出了經驗公式。

從研究現狀發現,目前針對陶瓷/金屬靶板的研究大多局限于陶瓷/鋼靶板,對于陶瓷/鈦合金靶板的研究鮮有報導,而鈦合金因其優異的耐腐蝕、耐高溫性能適合用于艦用復合裝甲的背板[11-15]。

本文利用有限元分析軟件ANSYS/LS-DYNA研究了7.5 g圓柱體彈侵徹不同厚度配比的陶瓷/鈦合金靶板的彈道極限速度及靶板的破壞模式,通過分析得到了彈道極限速度隨陶瓷厚度和鈦合金厚度變化的經驗公式,探討了陶瓷和鈦合金厚度配比對結構抗彈性能的影響規律。

1 有限元模擬

1.1 模型建立

利用有限元軟件ANSYS/LS-DYNA,對高速圓柱體彈侵徹陶瓷/鈦合金結構進行數值模擬研究。彈體選用長度15 mm,直徑9 mm的圓柱體彈,結構中陶瓷平面尺寸為100 mm×100 mm,鈦合金板平面尺寸為300 mm×300 mm。彈體、陶瓷以及鈦合金板均采用8節點的Solid 164三維實體單元,采用Lagrange網格建模。彈體沿長度方向劃分為15個網格,直徑方向劃分為12個網格;陶瓷和鈦合金板沿厚度方向按每毫米1層均勻劃分,面內網格在侵徹區加密,向四周稀疏過渡。數值模型采用cm-g-μs單位制。有限元模型(4 mm陶瓷+4 mm鈦合金)如圖1、圖2所示。

圖1 有限元整體模型

圖2 有限元模型剖面圖

彈體材料為35CrMnSiA 低合金超高強度鋼，采用* MAT_PLASTIC_KINEMATIC 雙線性彈塑性本構模型，模型應變率效應由Cowper-Symonds 模型描述，材料參數如表1 所示。表中，ρ為密度;μ為泊松比;σy為靜態屈服強度;E為彈性模量，Eh為硬化模量;D和N為常數，對于低碳鋼，通常取D= 40s-1，N= 5。

表1 彈體鋼的材料模型參數

SiC陶瓷采用Johnson-Holmquist_ceramics材料模型和Gruneisen狀態方程來描述,材料參數如表2所示。表中,G為剪切模量;A為無損標準強度參數,B為斷裂標準強度參數;c為應變率系數;m為斷裂強度指數,n為無損強度指數;D1為第一斷裂參數,D2為第二斷裂參數;K1,K2,K3為常數。

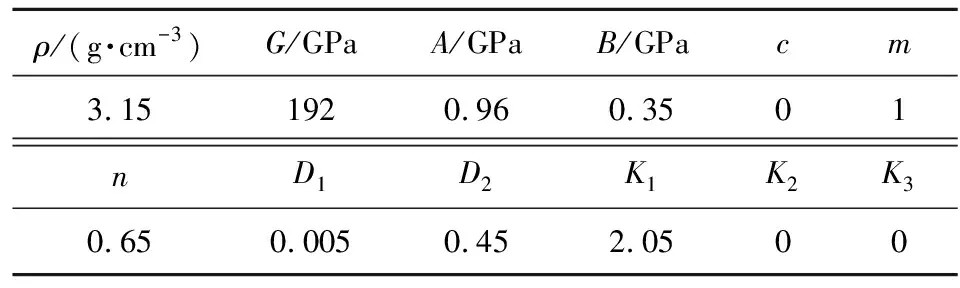
表2 SiC陶瓷的材料參數

鈦合金采用Johnson-Cook材料模型[16]和Gruneisen狀態方程來描述,材料參數如表3所示。表中,A1為靜態屈服強度;B1為應變硬化模量;n1為應變硬化指數;m1為熱軟化指數;Tm為材料的熔點,T0為參考溫度(取室溫);D1～D5為常數。

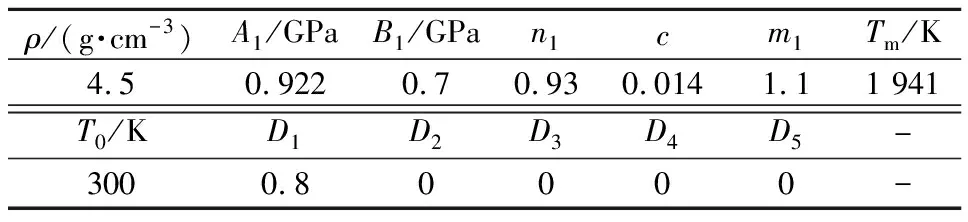
表3 鈦合金材料參數

1.2 算法驗證

文獻[17]開展了7.62 mm及12.7 mm穿甲彈侵徹陶瓷/鈦合金結構的試驗,通過以上材料模型建立相應的數值仿真,與試驗結果進行了對比,如表4所示。表中,C表示陶瓷,T表示鈦合金,字母前數字表示厚度,如10C/3T表示10 mm陶瓷+3 mm鈦合金結構。由表4可以看出,數值計算結果得到的鈦合金板穿深與試驗結果的誤差均小于10%,認為1.1節中材料模型較為合理。

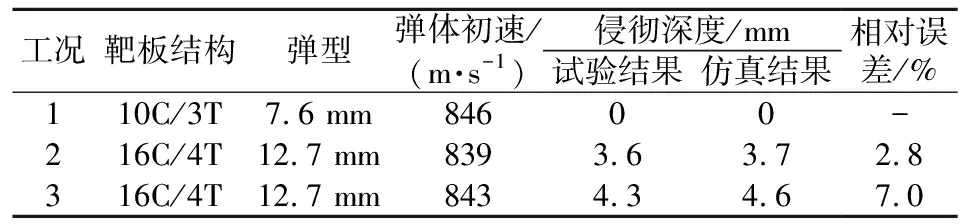
表4 數值計算結果與試驗結果對比

2 數值計算結果與分析

2.1 陶瓷和鈦合金厚度變化對結構破壞變形的影響

為研究靶板彈道極限速度及破壞模式隨陶瓷厚度和鈦合金厚度的變化關系,針對靶板結構I:3mmSiC陶瓷+鈦合金,鈦合金厚度dT分別取3 mm,4 mm;結構Ⅱ:4 mmSiC陶瓷+鈦合金,dT分別取2 mm,4 mm,6 mm,8 mm;結構Ⅲ:5 mmSiC陶瓷+鈦合金,dT取4 mm,5 mm,通過數值仿真對以上8種工況進行計算,得到了不同靶板結構下的彈道極限速度v50及彈道極限速度附近結構破壞后的變形情況,具體結果如表5所示。圖3為工況2、工況4、工況5中靶板的破壞形貌圖。

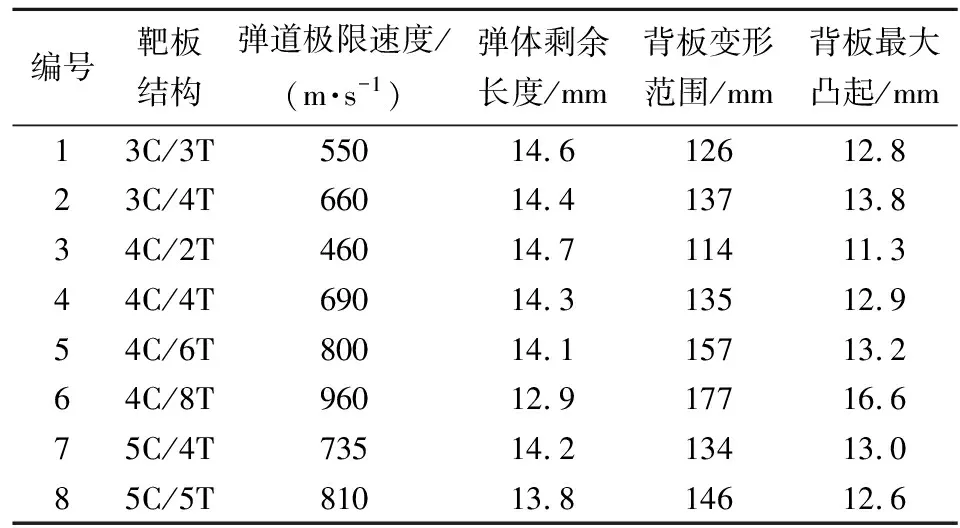
表5 不同結構在彈道極限速度侵徹下的數值計算結果

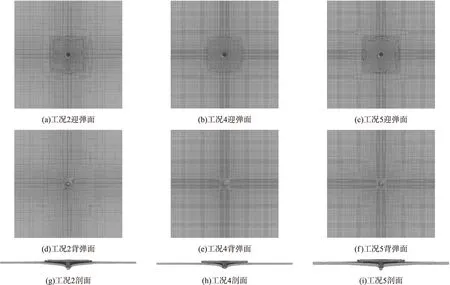
圖3 靶板破壞形貌

結合表5、圖3發現,當彈體速度接近彈道極限速度時,陶瓷/鈦合金結構的破壞變形程度基本隨著結構厚度增加而增大,并且彈道極限速度越大,靶板變形程度越大。進一步分析表5,對比工況2、工況4、工況7及工況3、工況4、工況5、工況6可以看出,增加鈦合金厚度對彈體侵蝕程度及靶板變形程度產生的影響大于增加陶瓷厚度。

觀察圖3中靶板迎彈面破壞形貌可知,由于陶瓷為非均勻性材料,彈體撞擊面板后極易在微孔洞處產生微裂紋,并在拉伸波作用下聚合擴展,最終使陶瓷面板斷裂失效,陶瓷破口尺寸大于彈體直徑,且陶瓷厚度越薄,彈體速度越高,陶瓷面板碎裂程度越嚴重;觀察靶板背彈面及剖面破壞形貌可知,當彈體速度接近彈道極限速度,鈦合金背板背彈面的破壞形貌呈現隆起-蝶形變形并伴隨細微裂紋,同時彈道極限速度越大,鈦合金靶板變形程度越大。

2.2 彈道極限速度隨陶瓷和鈦合金厚度的變化關系

表5給出了不同厚度下陶瓷/鈦合金結構的彈道極限速度,對比3C/4T,4C/4T,5C/4T結構發現,在dT保持不變的情況下,陶瓷/鈦合金結構的彈道極限速度隨陶瓷厚度dC的增加基本呈線性增長的變化趨勢,通過線性擬合,得到彈道極限速度v50隨陶瓷厚度dC的變化公式如式(1);對比4C/2T,4C/4T,4C/6T,4C/8T結構發現,在dC保持不變的情況下,陶瓷/鈦合金結構的彈道極限速度隨dT的增加同樣呈線性增長的變化趨勢,通過線性擬合,得到彈道極限速度v50隨鈦合金厚度dT的變化公式:

v50=37.5dC+545

(1)

v50=80.5dT+325

(2)

通過式(1)、式(2)可分別計算得到不同陶瓷厚度與4 mm鈦合金板組合結構、4 mm陶瓷與不同厚度鈦合金板組合結構的彈道極限速度。圖4、圖5分別為彈道極限速度隨陶瓷厚度、鈦合金厚度變化的擬合曲線,對比仿真結果與擬合結果可知,最大相對誤差的絕對值為6.9%,因此用式(1)、式(2)來計算陶瓷厚度、鈦合金厚度變化引起的彈道極限速度變化是可靠的。

由圖4、圖5顯示的彈道極限速度隨靶板厚度變化的規律并結合式(1)、式(2)對于彈道極限速度的預測公式,可知陶瓷與鈦合金厚度變化對彈道極限速度的影響有所差別:式(1)表示在鈦合金厚度保持不變的情況下,增加1 mm陶瓷,結構的彈道極限速度隨之增加37.5 m/s;式(2)表示在陶瓷厚度保持不變的情況下,增加1 mm鈦合金,結構的彈道極限速度隨之增加80.5 m/s。因此當陶瓷和鈦合金同時發生厚度變化時,彈道極限速度隨之變化的公式表達為

v50=37.5dC+80.5dT+P

(3)

式中:P根據仿真結果擬合得到,P=161.3。

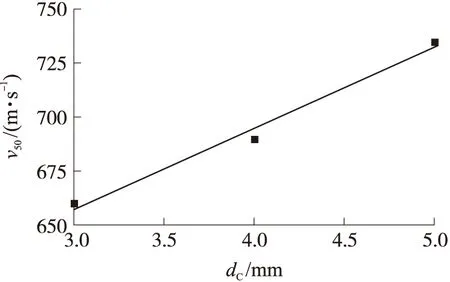
圖4 彈道極限速度隨陶瓷厚度的變化擬合曲線

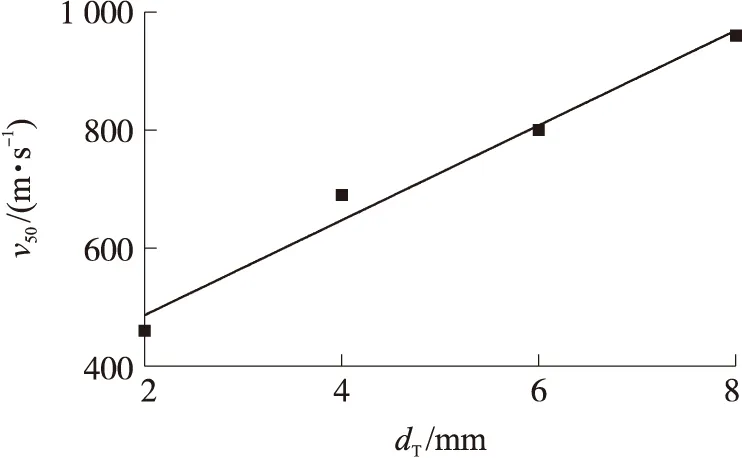
圖5 彈道極限速度隨鈦合金厚度的變化擬合曲線

綜上所述,得到7.5 g圓柱體彈侵徹下,任意厚度陶瓷/鈦合金結構的彈道極限速度計算公式:

v50=37.5dC+80.5dT+161.3

(4)

為驗證擬合公式的準確性,對靶板結構3C/5T,3C/6T,4C/5T,4C/7T,5C/3T,5C/6T進行數值模擬計算,對比了6種結構在仿真計算下及擬合公式計算下的彈道極限速度,結果如表6所示。

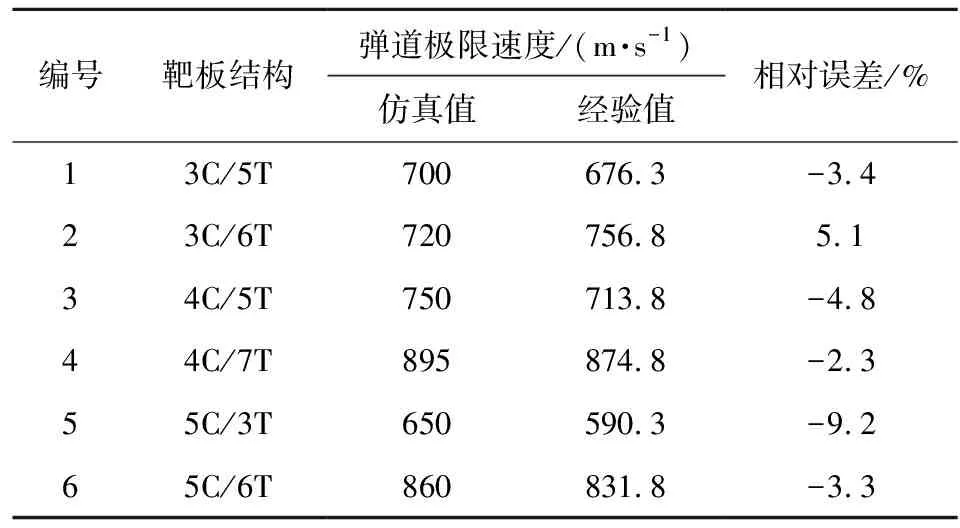
表6 數值計算結果與擬合公式計算結果的對比

表6中以仿真結果為基準,擬合公式得到的彈道極限速度與仿真值的相對誤差絕對值均小于10%,因此該擬合公式能合理預測陶瓷/鈦合金結構的彈道極限速度。

2.3 陶瓷/鈦合金厚度比對結構抗侵徹性能的影響

陶瓷/鈦合金厚度比變化會影響彈體侵蝕程度、鈦合金靶板的變形程度,進而影響陶瓷/鈦合金結構的抗彈性能。為研究陶瓷/鈦合金厚度比對結構抗侵徹性能的影響規律,定義彈體初速為1 000 m/s,選取陶瓷厚度為3 mm,4 mm,5 mm,6 mm,鈦合金厚度由1 mm,依次增加1 mm,直至7 mm,通過對以上工況進行數值模擬計算,得到不同靶板結構下彈體的剩余速度及單位面密度吸能,具體結果如表7所示。

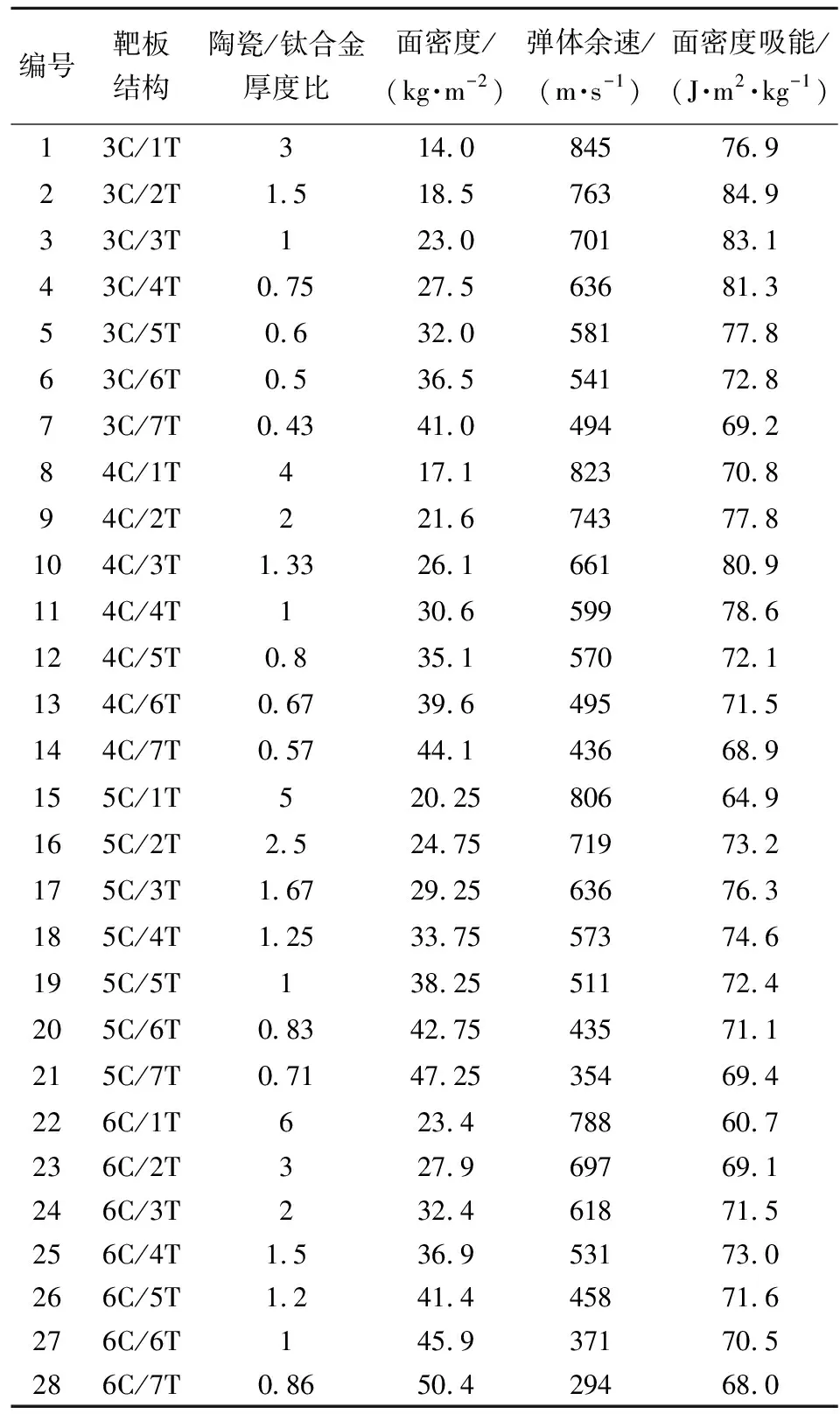
表7 不同陶瓷/鈦合金厚度比時結構抗侵徹數值計算結果

根據表7中的數據繪制靶板單位面密度吸能EA隨陶瓷/鈦合金厚度比的變化曲線,如圖6所示。觀察圖6發現,陶瓷/鈦合金結構的單位面密度吸能隨陶瓷/鈦合金厚度比的增大先增大后減小;在各陶瓷厚度下,結構單位面密度吸能分別在陶瓷/鈦合金厚度比為1.5,1.33,1.67,1.5時出現峰值。因此認為當陶瓷/鈦合金厚度比在1～2之間時,結構抗彈性能較好。

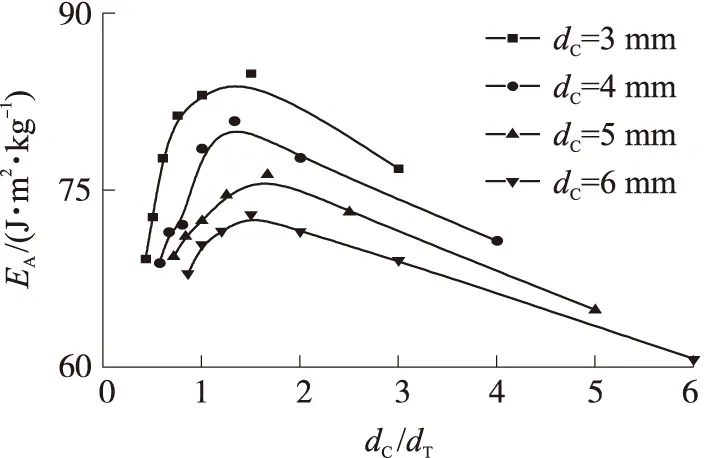
圖6 單位面密度吸能隨陶瓷/鈦合金厚度比的變化曲線

由圖6可知,當陶瓷/鈦合金厚度比較小時,結構的單位面密度吸能隨厚度比的增大而增大,這是由于陶瓷厚度太小,無法充分碎裂、侵蝕彈體,彈體破壞吸能較小,分散沖擊載荷作用較弱,且鈦合金背板受撞擊時彈速仍然較高,背板無法充分變形,導致吸能也較小。隨著厚度比的增大,單位面密度吸能達到一個極大值,此后單位面密度吸能隨厚度比的增大而減小,原因是背板厚度太小,無法對陶瓷面板形成有力支撐,陶瓷過早失效同樣無法充分碎裂彈體。

3 結論

本文利用有限元分析軟件ANSYS/LS-DYNA進行數值模擬,研究了7.5 g圓柱體彈侵徹不同厚度配比的陶瓷/鈦合金靶板的彈道極限速度及靶板的破壞模式,探討了陶瓷和鈦合金厚度配比對結構抗彈性能的影響規律,得到如下主要結論:

①陶瓷/鈦合金結構的破壞變形程度基本隨著結構彈道極限速度的增大而增大,并且增加鈦合金厚度對彈體侵蝕程度及靶板變形程度產生的影響大于增加陶瓷厚度。

②得到了7.5 g圓柱體彈侵徹任意厚度陶瓷/鈦合金靶板的彈道極限速度擬合公式,將仿真計算結果與擬合公式計算結果進行對比,認為該擬合公式能合理預測陶瓷/鈦合金結構的彈道極限速度。

③結構的單位面密度吸能基本隨陶瓷/鈦合金厚度比的增大呈先增大后減小的趨勢,當陶瓷/鈦合金厚度比在1～2之間時,結構抗彈性能較好。

本文得到的結論為艦船舷側防彈所需要的陶瓷和鈦合金厚度提供了參考,下一步將繼續開展相關試驗研究。