三維實李代數的分類
2020-07-06 04:30:36胡建華栗菲菲
上海理工大學學報 2020年3期
胡建華, 栗菲菲, 劉 靜
(上海理工大學 理學院,上海 200093)
李代數的分類問題是李代數結構理論的核心內容。經典的李代數理論[1-3]利用根系理論完整地給出了特征為0的代數閉域上的有限維半單李代數分類。但對于特征為或非代數閉域上的李代數分類還有許多未解決的問題。而對于這些李代數的研究,總是從低維開始的。文獻[4-7]利用同構定理研究了低維的可解李代數和冪零李代數分類問題。實數域是特征為0的數域,但它是非代數閉域,因此,實李代數的結構與復李代數的完全不同。本文研究三維實李代數的分類問題,利用同構定理,根據導代數的維數[8-10]給出三維實李代數的完整分類。
1 基礎知識

定理1[1]令和是2個維 李代數,,若它們存在一組對應基,其對應的結構常數相等,則和同構。
同構的2個李代數,它們的導代數的維數相同。
文獻[1,3]在同構意義下給出了一維、二維實李代數的分類。一維實李代數只有一類,,是交換李代數,滿足,記為。二維實李代數有兩類。一類是交換的,滿足,記為;另一類是非交換的,滿足,記為。
現根據導代數的維數分別討論三維實李代數在同構意義下的分類。
2 三維實李代數的分類
2.1 導代數維數為0和1

2.2 導代數維數為2





2.3 導代數維數為3


最后,將以上關于三維實李代數的討論總結為定理2。
定理2 在同構意義下,3維實李代數有如下8類:
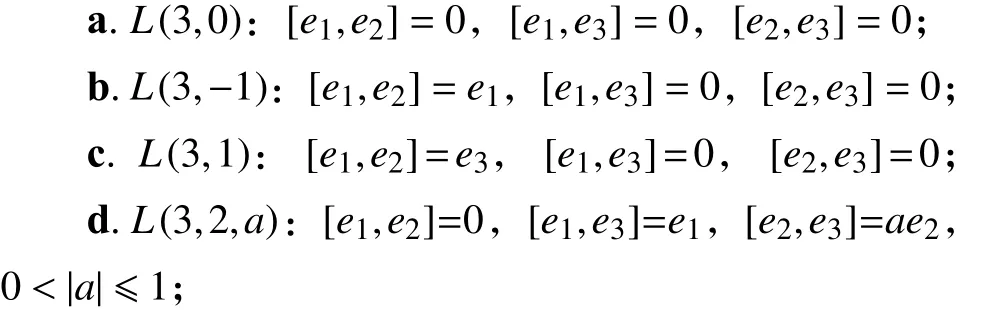

猜你喜歡
新少年(2022年9期)2022-09-17 07:10:54
數學小靈通(1-2年級)(2021年4期)2021-06-09 06:25:56
小天使·一年級語數英綜合(2020年6期)2020-12-16 02:56:41
瘋狂英語·新策略(2019年10期)2019-12-13 08:43:28
當代陜西(2019年10期)2019-06-03 10:12:04
中學生數理化·七年級數學人教版(2019年4期)2019-05-20 10:06:32
中學生數理化·七年級數學人教版(2018年6期)2018-06-26 08:36:06
初中生世界·七年級(2017年9期)2017-10-13 22:27:46
數學小靈通·3-4年級(2017年9期)2017-10-13 08:10:54
北極光(2014年8期)2015-03-30 02:50:51

