基于復合巖體的邊坡錨桿支護數值模擬

湯振山

（中鐵開發投資集團有限公司，云南 昆明 650000）

0 引言

錨桿支護是巖土工程支護必不可少的支護手段[1]，廣泛應用于工程基坑、采礦巷道、公路地鐵隧道等巖土工程實踐。錨桿支護強度是否合理不僅影響著工程的安全生產，還對工程成本的節約有著重要影響[2]，因此，準確確定錨桿支護效果，進而為支護參數的確定提供依據，具有重要意義。

長期以來，對于錨桿支護效果的數值計算，一般采用有限單元法，它以桁架、梁等桿單元形式模擬加固錨件，反映其剛度貢獻和對巖體的預壓作用[3]。但由于有限元法采用的是位移協調模型，錨桿單元必須布置于單元的邊上，而且錨桿單元的節點與巖體單元的節點必須重合。而模擬計算時因支護錨桿的幾何參數(如長度、傾角、傾向等)受有限元網格的制約，一般很難完全仿真各種錨桿復雜的幾何布局。致使錨桿支護的有限元模擬計算難度較大且計算效果不理想。

鑒于此，本文引入錨桿支護下復合巖體強度參數的定義，采用Abaqus 大型有限元分析軟件，對開州湖特大橋3#主塔基坑錨桿支護效果開展數值模擬研究，以期為錨桿支護下巖土工程巖體的模擬計算及有關工程實際提供參考。

1 工況概述

開州湖特大橋位于貴州省貴陽市開陽縣境內，橫跨洛旺河峽谷，甕安岸位于甕安縣米坪鄉大坪村內，開陽岸位于開陽縣馮三鎮墮秧村內。新建開州湖特大橋的3#主塔基礎為左、右分離式的基礎形式，承臺中心里程為K35+525，兩承臺間距17.45m。主塔承臺厚7m，平面尺寸為20.5m×20.5m。3#主塔區域石方占比較大，由地勘報告可知邊坡開挖巖層多為中風化白云質灰巖。

基坑以巖質邊坡為主，最高側分三級坡，每級坡高10m，邊坡采用錨噴支護——全粘結錨桿+掛網噴射砼支護，錨桿豎向間距為2m，水平間距為2m，錨桿長度為3m，鉆孔直徑為70mm，采用M30 水泥漿灌注。邊坡掛網采用6.5mm 鋼筋網，每2m 設置一道16mm 加勁鋼筋，坡面噴射混凝土分2 層噴射，每層厚度5cm（共厚10cm）。基坑邊坡支護形式如圖1所示。

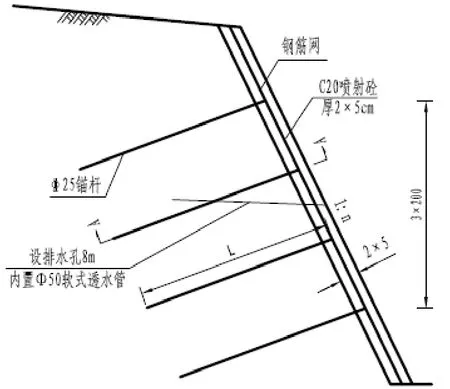
圖1 基坑邊坡支護形式示意

2 理論基礎

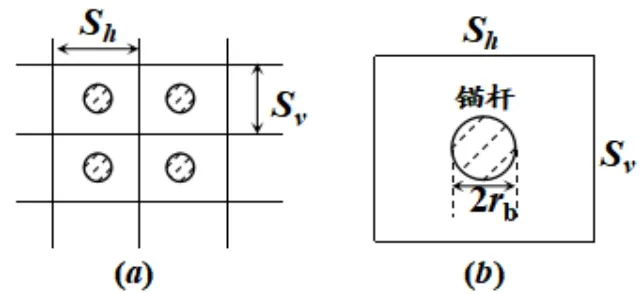
由于采用常規桁架單元等方式對加固錨桿進行直接模擬的效果不理想，為此，本文采用均勻化方法將錨桿與邊坡巖體等效成均質的復合巖體，并引入能夠反映基坑邊坡支護參數的錨桿密度因子來描述復合巖體的等效強度，錨桿密度因子定義為(錨桿為螺紋錨桿)[4]

式中，β為錨桿強度因子，無量綱標量；Sv為錨桿豎向間距，2m；Sh為錨桿水平排距，2m；rb為錨桿半徑，0.0125m；L為去剛量化單位長度，L=1m；φ為邊坡巖體內摩擦角，度。

應當指出：錨桿密度因子β在文獻[5-7]中均被錯誤地定義為量綱是m-1的參量。因此本文在其基礎上乘以單位長度L(即1m)加以修正，使其無量綱化。

基于均勻化方法對錨桿支護后復合邊坡巖體的等效強度進行定義，其中，等效彈性模量E*定義為

式中，Eb為錨桿彈性模量，為200GPa；E為邊坡巖體彈性模量，GPa。

而復合巖體的等效內聚力C*和等效內摩擦力φ*分別為

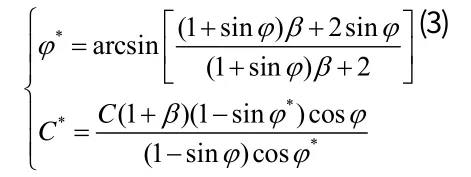
式中，C為基坑邊坡巖體黏聚力，MPa。

如表1所列，為開州湖特大橋3#主塔基坑邊坡巖體有關參數，將其帶入式(1)～(3)可分別得到錨桿支護作用下的復合巖體彈性模量、黏聚力和內摩擦角，匯入表1末行。

表1 材料屬性

此外，復合巖體在基坑邊坡的深度應與錨桿長度相等，即為3m，如圖5所示。

3 數值模擬分析

本文數值模擬分析采用Abaqus 軟件進行，該軟件是目前國內外通用大型有限元計算分析軟件之一[8]，由美國Abaqus 公司于1978年推出，在全球工業界內，現已被公認為是一套解題能力最強、分析結果最可靠的軟件[9]。模擬計算主要包括以下幾個步驟。

3.1 建模與材料定義

根據開州湖特大橋3#主塔基坑鉆探、地質資料及埋深等因素，在綜合考慮計算復雜程度及計算機存儲空間的前提下，以橋梁中心線為對稱軸建立寬×高=30m×45m 的二維對稱模型(如圖3所示)，用以模擬錨桿支護對基坑邊坡穩定性的影響。為使模擬分析具有可比性，本文采用兩種形式對基坑邊坡錨桿支護的效果進行模擬計算：①利用常規桁架單元模擬加固錨桿(下文稱之為“模擬方法I”)；②采用錨桿密度因子換算成復合圍巖強度參數的方法模擬加固錨桿(下文簡稱為“模擬方法II”)。模型巖體破壞遵循Mohr-Coulomb 準則，模擬輸入的巖體材料基本參數如表1所列。

3.2 邊界條件與施加載荷

模型頂部邊界為地表，無需施加荷載，底邊界設置豎直方向位移為0，左邊界設置水平方向位移為0，右邊界設置對稱約束，模型尺寸及邊界條件如圖3所示。

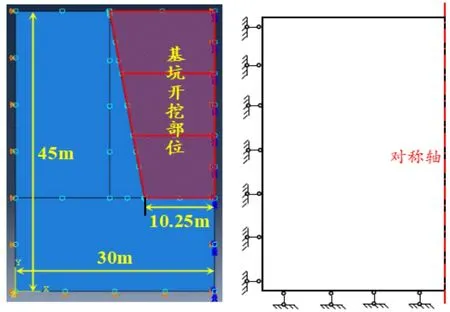
圖3 模型尺寸及邊界條件

3.3 網格劃分

采用4 節點雙線性4 邊形平面應變單元將模型劃分為5772 個單元，同時，為了兼顧計算精度與計算機存儲空間，對基坑邊坡周邊的單元進行細化，單元劃分整體呈內密外疏的輻射狀，輻射基數為5。

3.4 模擬計算

模擬計算過程大致分成以下3個基本步驟：

①初始地應力平衡

由于模型為規則的矩形，簡單添加關鍵詞即可實現[10]，重力加速度取9.8N/Kg，側壓系數取為1.0。由圖4可知，原巖應力施加后模型內的位移很小，其數量級為10-6。也就是說，原巖應力在模型內引起的位移很小，符合計算要求，可進行后續計算。

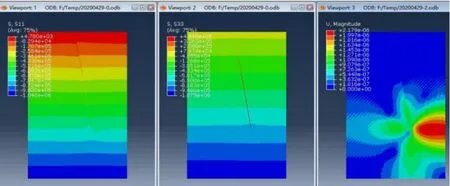
圖4 地應力平衡結果

②基坑開挖

按照工序，通過建立3個開挖塊的幾何集合，依次采用單元生死技術實現基坑的開挖。

③基坑支護模擬

基坑開挖后，采用前述兩種方式對基坑邊坡錨桿支護分別進行模擬計算，模擬形式如圖5所示。

圖5 兩種錨桿模擬形式

3.5 計算結果分析

如圖6所示，分別為開州湖特大橋的3#主塔基坑邊坡在無支護、錨桿支護模擬方法I 和錨桿支護模擬方法II 條件下模型水平位移分布的情況。分析該圖可知，錨桿支護對于模型整體的位移分布具有一定的改善效果，但就基坑坡面的水平位移而言，錨桿模擬方法I 與無支護條件下的情況幾乎完全一致，支護效果幾無體現。

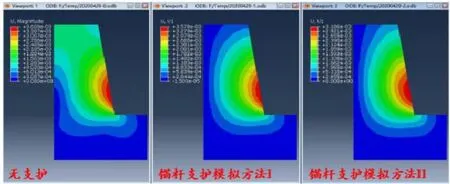
圖6 不同條件下模型水平位移分布

為定量分析各條件下基坑坡面的水平位移分布情況，沿坡面從坡肩到坡趾均勻地取100 個節點，將不同計算條件下各節點的水平位移繪制成曲線，如圖7所示。

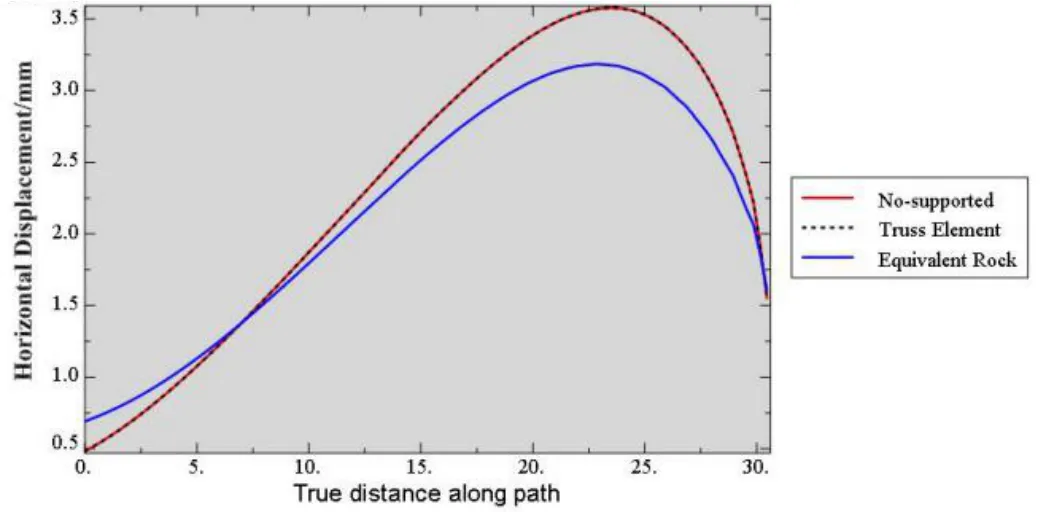
圖7 不同算法的坡面節點水平位移分布

由圖7可知，采用桁架單元直接“嵌入錨桿”的模擬方法I 的計算結果幾乎和無支護下的結果完全一致(經多次細化錨桿單元處理后，情況不變)，也即是說，錨桿的支護效果幾乎完全未模擬出來；而采用“復合巖體”的模擬方法II 的計算效果較好。

4 結論

通過引入并修正能夠反映基坑邊坡錨桿支護參數的錨桿密度因子，采用均勻化方法得到錨桿支護后復合巖體的等效強度參數，對于相關理論研究和工程設計具有一定參考意義。

常規的桁架單元用于模擬加固錨桿時，需考慮錨桿單元與巖體單元的匹配問題，模擬計算較復雜且模擬效果很差；而本文給出的“復合巖體”的計算模型，考慮了對邊坡巖體彈性模量、黏聚力及內摩擦角等基本參數的增強，方法簡單便捷且模擬效果較好。