城市地下綜合管廊通風縮尺模型的相似性研究
徐元寶
(山西省城鄉規劃設計研究院工程設計中心,030010)
1 城市地下綜合管廊通風系統縮尺模型建立
根據相似理論要求,需要對城市地下綜合管廊的通風系統進行新的界定,在了解原型以及模型各邊界條件及其物理參數的基礎上,采用Fluent 軟件構建模型,該模型能夠分別模擬不同工況,并通過計算的方法做出相似性判斷,這樣才能為指導后續研究提供必要的支持[1]。
1.1 案例簡介
選擇本地區某綜合管道任意一段的通風區間為原型。該案例的區間總長度為200m,長寬均為3m,艙室兩側布置電纜,墻壁上各有5 條回路,采用平行布置方法,上下相鄰電纜之間的間距為0.5m;在進風口位置布設風機,該風機能夠持續地向綜合管廊內提供風力,以艙室內部為風道,流動到排風口后將風力傳送到外側;電纜在送電期間會產生一定的熱量而影響空氣溫度,但因為墻壁以及空間結構傳導的影響,部分熱量會通過墻壁面直接發散到土壤中。
1.2 控制方程的構建
根據相似理論的相關內容可知,為了保障縮尺模型與原型具有一致性,則設計人員必須考慮兩個重要的相似條件,分別為:(1)幾何相似條件。所構建的縮尺模型應該嚴格按照原型的尺寸遵照特定比例縮小,這樣才能滿足幾何相似的要求,本次研究中將采用了1:5 的方法縮小原型。(2)運動相似性。確保縮尺模型所處環境相同,這樣模型的仿真結果才能對原型的管理、建設有益。對模型的相似參數進行推導,期間原型與模型之間的控制方程要確保具有一致性。之后在描述方程流動轉熱過程中,控制方程需要充分考慮不同工況下的要求,所以本文本文提出了一種連續方程控制模式,其關系式為:
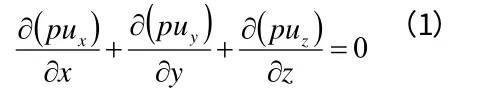
在方程式(1)中,xuyuzu分別代表在X 軸、Y 軸、Z 軸上的速度,其單位為m/s;p為密度,單位為kg/m3;?為導熱系數,單位為W/(m·°C)。
1.3 邊界條件參數比例的確定
Gr 準則可以用于判斷自然對流的條件,在該案例中,本文考慮到浮升力等因素會帶來氣流變化,在強制對流條件下適當忽視Gr 對地下綜合管廊的影響,并在其他外部條件基本相同的情況下,通過Fluent 軟件做數值運算,判斷假設的正確性。
2 數值仿真計算
2.1 模型簡化
考慮到本案例管廊的具體情況,采用模型簡化方法能夠進一步降低數據分析難度,所以在簡化模型期間,可以針對模型做出以下判斷:
(1)該模型具有良好的穩定性,尤其是當放熱量與散熱量實現平衡的情況下,其溫度場的分布會隨著時間的變化而發生改變。(2)電纜支架受空間因素的影響小,所以在模型分析期間可以忽略電纜以及電纜支架幾何結構的影響。
在此基礎上,結合原型的數據構建縮尺模型,則幾何結構與原型結構之間的參數對比結果如表1所示。

表1 幾何數據的對比結果(單位:m)
2.2 邊界條件的實現
通過數據計算的方法能夠描述流體流動的傳熱過程,并確定其中數據預算的要求,要注意確保運算過程的控制方向滿足相似理論中所提到的控制方程[2]。
所以在數據運算環節,本文采用湍流模型以及空氣模型的要求,在考慮地下綜合管廊通風特性的基礎上,評價受熱、浮生力等因素對傳熱的影響,所以本文縮尺模型中空氣的關鍵物理參數為:密度1.225kg/m3,比熱容1006.4J/(kg·°C),導熱系數0.0219W/(m·°C)。其中邊界條件的設計要求為:在進出風口的設計上,采用了機械通風+自然通風的方法,其中進風口為速度進邊界條件,排風口為壓力出邊界條件。
3 實驗內容與方法
3.1 實驗測量內容與測量設備
為了能夠有效模擬地下綜合管廊通風縮尺模型的相關指標,判斷任意端面的平均風速等數據,在模型的基礎上設置了6 個斷面,采用全壓差測量方法檢測每個斷面的狀態。
所采用的測量設備包括壓差傳感器、風速傳感器等,測量數據依靠數據采集模塊提取,其采集軟件為LABVIEW。
3.2 縮尺模型的平均風速
在不同類型鍛煉中,地下綜合管廊艙室在任意環境下的通風風速會發生明顯變化,根據模型的仿真結果可以發現,在進、排風口位置,考慮到此處兩端的斷面小,風速大;而艙室內部的斷面大、風速相對較小,這種情況會導致艙室內部壓力呈現出不同的變化趨勢。
所以為了可以了解縮尺模型在進出風口位置的局部阻力以及艙室沿程阻力特性,將需要進一步判斷各個區段的范圍區間,根據不同時間段的風速監測結果發現,平均風速的偏差值波動區間為6%-10%,而因為風速的穩定性與準確性正相關,因此選擇偏差更小的斷面進行沿程阻力判斷。最后的判斷結果顯示,在管線面積占比最大的情況下,其有效通風面積越小,反之亦然;相同流量條件下,發現其他斷面的監測結果也發現,其他斷面的平均風速與頻率基本相同,最終的監測結果如圖1所示。
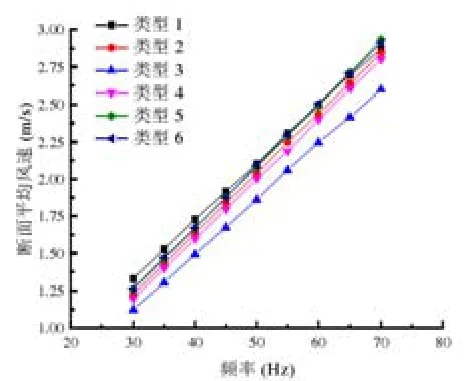
圖1 不同斷面下測量的平均風速
根據圖1的相關資料可發現,除了斷面3 之外,其他五個斷面的風速基本相同。
3.2 熱力相似性分析結果
在熱力相似性分析結果中,各個斷面的平均溫度使用Fluent 軟件來計算每個斷面的溫度變化,所以在本次研究中,通過直接從軟件計算中調用平均溫度結果,并分析縮尺模型與原型之間的相似性,這種方法能夠進一步降低數據處理難度。
在本次研究中發現,縮尺模型與原型之間的溫度分布基本相同,其中從進風口到排風口位置,空氣因為電纜的加熱效果會造成斷面平均溫度的變化。因此可判斷縮尺模型與原型之間的對應關系式基本相同的,縮尺模型的誤差得到了有效控制。因此本文將采用公式(2)來計算其中的相對誤差。
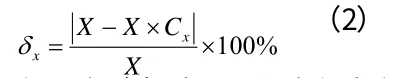
在公式(2)中,X 代表任意參數,包括阻力系數、溫度、速度等;Cx為對應參數的比例系數。
之后對原型與縮尺模型的溫度分布云圖來判斷兩者溫度場的相似性,通過云圖的比較結果可發現,原型與縮尺模型之間沿著流動方向,其空氣溫度逐漸升高,并且在同一對應的斷面上,兩者之間的云圖表現基本相同,并且靠近電纜位置的溫度更高,證明該縮尺模型是科學有效的。
結束語本文介紹的縮尺模型方法具有可行性,概模型的仿真結果與原型基本相同,因此認為該縮尺模型具有極高的相似性,能夠為未來城市地下綜合管廊通風設計提供支持,值得進一步推廣。

