差分進化算法在數字PID參數整定中的應用
孟亞男,馮 兼
(吉林化工學院 信息與控制工程學院,吉林 吉林 132022)
在工業(yè)過程控制中,PID控制策略應用十分廣泛,它關系到控制系統(tǒng)性能的優(yōu)劣[1].而PID控制系統(tǒng)最核心的部分,就是其控制參數.自PID算法問世以來,最普遍的問題就是如何優(yōu)化整定其控制參數.根據發(fā)展階段可以劃分為常規(guī)整定和智能整定兩大方法,在工業(yè)生產中常用的有經驗法(試湊法)、衰減曲線法和響應曲線法.在實際生產中,大多數都是根據經驗來進行整定.這難免會費時費力,造成一定程度上的浪費,降低生產效率.針對上述問題,介紹一種利用差分進化算法優(yōu)化整定PID控制參數的方法,仿真結果表明,該方法提高了參數的整定速度和準確度,基本達到了控制的要求.
1 數字式PID控制原理
數字PID是利用計算機軟件程序來模擬PID控制算法,數字控制屬于采樣控制,需要對連續(xù)型PID算法做離散化處理.理論上滿足采樣周期足夠短,則離散型控制算法便可以近似處理為連續(xù)型控制算法,使控制過程更加靈活實用.經離散化處理后,連續(xù)型PID算法各部分可分別用式(1)、(2)、(3)近似替代.
t≈kT,
(1)
(2)
(3)
則離散PID表達可寫成式(4)形式:
(4)
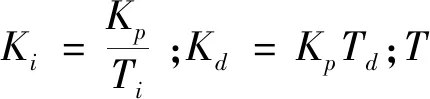
數字PID主要分為增量式算法和位置式算法,理論上二者是相同的,但當進行數字量化處理后,二者的實現過程會有所差異.以增量式為例,雖然可以降低誤動作的影響,但由于模型的限制,可能會引起較為嚴重的方法誤差,積累到一定程度時會使系統(tǒng)輸出嚴重偏離期望值.綜合考慮,本文選用位置型PID算法,方框圖如圖1所示.

圖1 位置式PID控制系統(tǒng)方框圖
2 差分進化算法
2.1 基本原理
差分進化算法(DE)屬于全局優(yōu)化算法范疇,其進化流程與遺傳算法相似,都是以種群進化為基礎的并行搜索算法[2],圖2為DE算法基本流程圖[3].一般需要先給定初始種群,計算群體個體適應度,進行初始化操作,再利用變異、交叉和選擇等方式不斷迭代更新種群,淘汰劣質個體,保留優(yōu)質個體,有利于逼近全局最優(yōu)解.
差分進化算法結構簡單且易于實現,特別在復雜系統(tǒng)的參數優(yōu)化問題上,DE算法的表現尤為突出,已經在工業(yè)控制等諸多領域得到了應用,實際效果較為滿意.
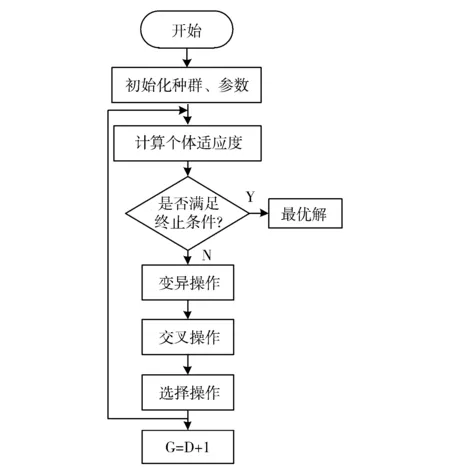
圖2 差分進化算法基本流程圖
2.2 參數設置
DE算法參數較少,易于理解與實現,主要包括種群規(guī)模M、變異算子F和交叉算子CR.變異算子F控制個體向量的擾動程度,決定全局尋優(yōu)的能力,一般為F=0.3~0.6;交叉算子CR反映了個體間信息交換的程度,一般為CR=0.6~0.9;種群規(guī)模M控制種群的多樣性和收斂速率,一般為M=20~50.三個主要的參數沒有固定取值,各個參數的選擇要根據算法的優(yōu)化目標適當選擇[3].
3 基于差分進化算法的PID整定
3.1 目標函數的選取
將“快速—無超調”的性能指標作為系統(tǒng)優(yōu)化整定的目標,在許多參數優(yōu)化的系統(tǒng)中,性能指標函數一般都是以系統(tǒng)的e(t)為泛函的積分形式所建立的[4].根據所要達到的性能指標,選擇合適的目標函數尤為重要.參考了IAE準則,選用式(5)作為性能指標.
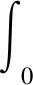
(5)
上式中,以誤差絕對值隨時間的積分為基礎,同時又引入了系統(tǒng)輸入的平方項,由于要求所優(yōu)化整定的系統(tǒng)無超調,采用懲罰功能,即當r(t)-y(t)=e(t)<0時進行優(yōu)化,將超調量作為最優(yōu)控制指標的一項,則式(5)可改寫為式(6)[5-7].
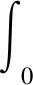
(6)
式中,e(t)為系統(tǒng)誤差;u(t)為控制器輸出;w1、w2和w3為權值.
3.2 Matlab實現差分進化算法PID整定
基于以上原理,利用Matlab編寫M函數文件進行實驗.被控對象的選擇如式(7)所示,令系統(tǒng)采樣時間Ts=0.001 s,將式(7)轉化成式(8)的差分方程形式;考慮到“快速—無超調”的控制要求,采用PID控制方案[8],輸入階躍響應yd=1,群體規(guī)模M=50,令F=1.7,CR=0.8.預先設置Kp∈[0,10],Ki∈[0,1],Kd∈[0,2],有利于全局最優(yōu)解的搜尋,降低盲目性,w1=0.999,w2=0.001,w3=10.取進化代數G為50.
(7)
y(k)=-den(2)*y_1-den(3)*y_2+num(2)*u_61+num(3)*u_62,
(8)
vi,G+1=ab,G+F·(ar1,G-ar2,G),
(9)
變異算子的程序實現:從種群中隨機取個體ar1,G、ar2,G和ar3,G,且b≠r1≠r2≠r3,以任意整數ri表示個體序號;則變異過程可寫成式(9)形式.最優(yōu)個體用ab,G表示,產生的新個體用vi,G+1表示.則Matlab程序實現如下:
for i=1:N
a=ai(i,:);
n1=1;n2=1;n3=1;n4=1;
while(n1==n2||n1==n3||n2==n3||n1==i||n2==i||n3==i||n4==i ||n1==n4||n2==n4||n3==n4 )
n1=ceil(size * rand(1));n2=ceil(size * rand(1));
n3=ceil(size * rand(1));n4=ceil(size * rand(1));
end
v(i,:)=BestS+F*(ai(n1,:)-ai(n2,:));
(10)
交叉算子的程序實現:交叉操作是為了維持群體的多樣性,有利于最優(yōu)解的搜索.具體操作參考式(10),式中rand∈[0,1],則Matlab程序實現如下:
for j=1:1:CL
tempr=rand(1);
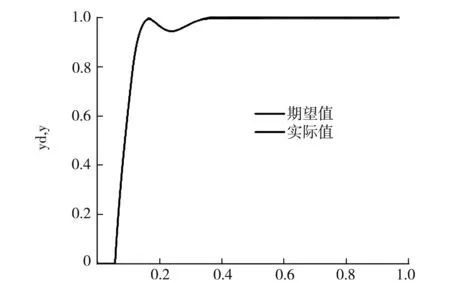
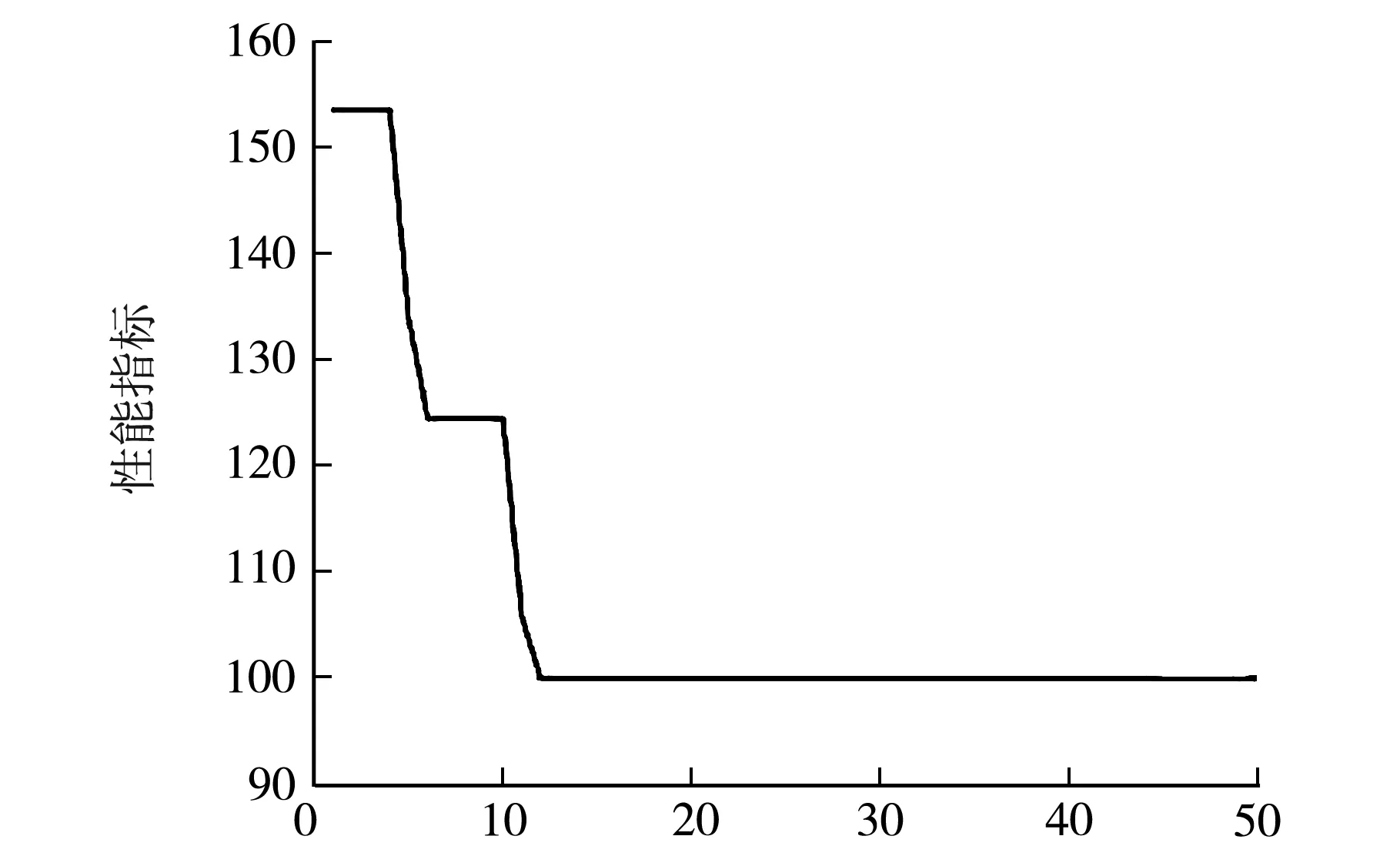
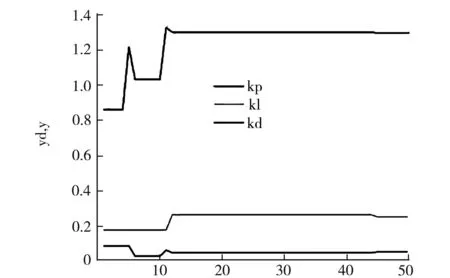
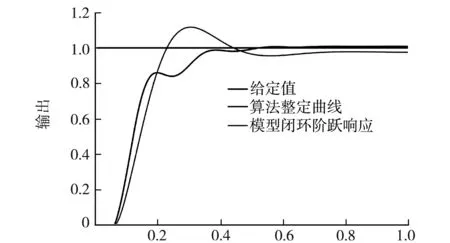
if(tempr u(i,j)=v(i,j); else u(i,j)=ai(i,j); end end (11) 選擇算子的程序實現:根據式(11)可知,分別將ui,G和ai,G代入適應度函數求取適應值進行比較,保留較小的個體[9-11],則Matlab程序實現如下: if(Model_1(u(i,:),BsJ) ai(i,:)=u(i,:); end 經過差分進化算法優(yōu)化整定后,得到實驗結果Kp=1.298 2,Ki=0.251 5,Kd=0.052 0,性能指標J=99.897 6,并在Simulink環(huán)境搭建控制器模型進行仿真,圖3為DE算法整定后的PID響應曲線,其上升時間約為0.35 s,調節(jié)時間約為0.486 s;圖4和圖5分別為性能指標函數J和控制參數的優(yōu)化趨勢曲線,從曲線可以得知,在進化代數為15之后趨于平穩(wěn);圖6為Simulink仿真曲線,未經優(yōu)化整定的曲線具有較大超調,約為11.72%,上升時間約為0.228 s,系統(tǒng)余差約為0.031.從仿真曲線中可以看出,采用差分進化算法進行參數整定,系統(tǒng)的各項性能指標較好,且基本達到了“快速—無超調”的目標,仿真結果較為理想. t/s圖3 算法整定后PID響應曲線 t/s圖4 性能指標函數J優(yōu)化趨勢 t/s圖5 Kp、Ki、Kd優(yōu)化整定趨勢 t/s圖6 Simulink仿真對比曲線 選用二階滯后傳遞函數作為被控對象,在Matlab中編寫DE算法進行PID參數的優(yōu)化整定,并將優(yōu)化后的數據應用在Simulink模型中,實現了基于差分進化算法整定PID參數的實驗與仿真.結果表明,DE算法的收斂速度快、搜索精度高,提高了系統(tǒng)參數整定速度和準確度,基本能達到預期指標.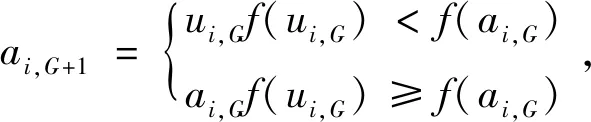
3.3 仿真結果
4 結 論

