正態(tài)分布產(chǎn)品的Bayes可靠性抽樣檢驗(yàn)方案
王燕飛
(吉林化工學(xué)院 理學(xué)院,吉林 吉林 132022)
可靠性抽樣檢驗(yàn)是通過檢查產(chǎn)品的樣本質(zhì)量來評(píng)價(jià)整批產(chǎn)品質(zhì)量.隨著科技進(jìn)步,產(chǎn)品的可靠性越來越高,應(yīng)用經(jīng)典統(tǒng)計(jì)方法制定的可靠性抽樣檢驗(yàn)方案的抽樣量較大.因此,人們?cè)絹碓街匾晳?yīng)用Bayes統(tǒng)計(jì)方法制定可靠性抽樣檢驗(yàn)方案,以便充分利用產(chǎn)品的各類可靠性信息,從而有效地降低可靠性試驗(yàn)的抽樣量.
在實(shí)際生產(chǎn)生活中,很多產(chǎn)品的性能指標(biāo)都服從正態(tài)分布,非常普遍.但關(guān)于正態(tài)分布產(chǎn)品的可靠性抽樣檢驗(yàn)的研究成果卻較少.馮文哲、劉琦基于0—1損失函數(shù)和兩類風(fēng)險(xiǎn)約束條件,研究了正態(tài)型指標(biāo)的復(fù)雜假設(shè)的Bayes可靠性驗(yàn)證試驗(yàn)設(shè)計(jì)[1].張碩云等對(duì)于正態(tài)型指標(biāo)的簡單假設(shè),利用Bayes方法基于兩類風(fēng)險(xiǎn)確定了樣本量[2].很多產(chǎn)品的指標(biāo)是要求在規(guī)格上限與規(guī)格下限范圍之間鑒定為合格,否則認(rèn)為不合格.關(guān)于正態(tài)型產(chǎn)品的雙側(cè)規(guī)格限情形的可靠性抽樣檢驗(yàn)問題,國家標(biāo)準(zhǔn)GB8053—87[3]沒有明確方案.國際標(biāo)準(zhǔn)ISO3951:1989(E)和國家標(biāo)準(zhǔn)GB6378—86只有圖方法,沒有數(shù)值方法.美軍標(biāo)MIL-STD-414和美國標(biāo)ANSI/ASqCZI 1.9也僅是得到近似的抽樣方案設(shè)計(jì).呂建華、吳啟光利用經(jīng)典統(tǒng)計(jì)方法,探討了綜合雙側(cè)規(guī)格限下方差未知的正態(tài)分布產(chǎn)品的可靠性抽樣檢驗(yàn)方案[3].
事實(shí)上,正態(tài)型產(chǎn)品的指標(biāo)值多數(shù)都為正值.這一信息往往被忽視.針對(duì)正態(tài)分布指標(biāo)的雙側(cè)規(guī)格限情形,研究了在總體方差已知,總體指標(biāo)的均值為正的前提下,根據(jù)Bayes理論,確定最大熵先驗(yàn)分布,并求得后驗(yàn)分布.利用生產(chǎn)方和使用方的兩類風(fēng)險(xiǎn)約束條件,確定最小抽檢樣本量,從而制定更加合理有效的抽樣檢驗(yàn)方案.最后通過實(shí)例說明其效果優(yōu)于經(jīng)典統(tǒng)計(jì)方法確定的抽樣檢驗(yàn)方案.
1 基于最大熵先驗(yàn)的正態(tài)指標(biāo)的可靠性抽樣檢驗(yàn)設(shè)計(jì)模型(MENBR)
假設(shè)產(chǎn)品的某性能指標(biāo)X服從正態(tài)分布N(μ,σ2).其中σ2已知,指標(biāo)均值μ>0.為了檢驗(yàn)該指標(biāo)均值是否達(dá)標(biāo),抽取樣本X1,X2,…,Xn,其觀察值為x1,x2,…,xn.
產(chǎn)品的生產(chǎn)方和使用方根據(jù)產(chǎn)品性能的可靠性要求,共同協(xié)商建立如下統(tǒng)計(jì)假設(shè):
H0:L≤μ≤U,H1:μ>U或0<μ 其中L為指標(biāo)值的規(guī)格下限,U為指標(biāo)值的規(guī)格上限.即產(chǎn)品指標(biāo)均值滿足L≤μ≤U時(shí)認(rèn)為合格,否則認(rèn)為不合格. 根據(jù)Bayes理論,為了對(duì)產(chǎn)品指標(biāo)進(jìn)行檢驗(yàn),需要利用指標(biāo)值的后驗(yàn)分布[4].首先依據(jù)一些先驗(yàn)信息確定μ的先驗(yàn)分布.根據(jù)以往歷史數(shù)據(jù)資料,容易得到μ的樣本均值,近似估計(jì)總體均值.若E(μ)=θ(μ>0),則除此之外沒有其他信息可用.那么在這樣的前提條件下,確定最“無信息”的先驗(yàn)分布是非常合理的,即最大熵先驗(yàn)[5]. 證明:根據(jù)文獻(xiàn)[4],可知,若滿足條件 Eπ[gk(μ)]=θk(k=1,2,…,m), 其中g(shù)k(·),μk(k=1,2,…,m)分別表示已知的函數(shù)和已知的常數(shù).則此時(shí)μ的最大熵先驗(yàn)分布為 其中π0(μ)為μ的無信息先驗(yàn). 當(dāng)λ1≥0時(shí),π(θ)=0.無意義;當(dāng)λ1<0時(shí),π(θ)=-λ1eλ1θ. 下面利用μ的先驗(yàn)分布及總體分布確定μ的后驗(yàn)分布,得到如下定理2. (1) 故T的邊緣分布為 則μ的后驗(yàn)分布為 對(duì)產(chǎn)品指標(biāo)進(jìn)行可靠性抽樣檢驗(yàn),對(duì)于生產(chǎn)方最關(guān)心的是:由抽樣得到批產(chǎn)品沒有通過檢驗(yàn),而產(chǎn)品的性能指標(biāo)值卻是合格時(shí)的風(fēng)險(xiǎn).換言之,在抽樣檢驗(yàn)統(tǒng)計(jì)量T∈W(W為檢驗(yàn)的拒絕域)時(shí)μ∈[L,U]的概率.則生產(chǎn)方所承擔(dān)的最大風(fēng)險(xiǎn)即為后驗(yàn)概率 對(duì)于使用方而言,最關(guān)心的是通過抽樣批產(chǎn)品通過檢驗(yàn),但產(chǎn)品指標(biāo)卻是不合格時(shí)的風(fēng)險(xiǎn).或者說,在抽樣檢驗(yàn)統(tǒng)計(jì)量T?W(W為檢驗(yàn)的拒絕域)時(shí)μ∈(-∞,L)∪(U,+∞)的概率.則使用方所承擔(dān)的最大風(fēng)險(xiǎn)即為后驗(yàn)概率 通常,生產(chǎn)方和使用方的最大風(fēng)險(xiǎn)分別限定在給定數(shù)值α和β值以內(nèi).由此可知,可靠性抽樣檢驗(yàn)方案的制定,就是求解方程組 (2) 從而確定最小抽檢樣本量.將方程組(2)稱為基于最大熵先驗(yàn)的正態(tài)指標(biāo)的可靠性抽樣檢驗(yàn)設(shè)計(jì)模型(MENBR). 對(duì)于模型MENBR,拒絕域W的確定尤為關(guān)鍵.根據(jù)Bayes假設(shè)檢驗(yàn)理論,當(dāng)后驗(yàn)概率 P(μ∈Θ1|T=t)≥P(μ∈Θ0|T=t) (3) 時(shí)拒絕原假設(shè)H0. 將后驗(yàn)分布(1)代入(3)中,化簡得: (4) 即當(dāng)T滿足(4)式時(shí),拒絕原假設(shè)H0,則此時(shí)的T的范圍即為拒絕域W. 為了求解拒絕域W,可以利用Matlab編程.具體編程步驟如下: 建立函數(shù) 2.編制兩個(gè)子程序: 子程序1: 子程序2: 3.運(yùn)行子程序1和子程序2,可以分別得到臨界點(diǎn)C1和C2. 通過Matlab程序搜尋結(jié)果可得到,T的拒絕域W=(0,C1)∪(C2,+∞). 下面將拒絕域W=(0,C1)∪(C2,+∞)代入方程組(2),即可得到最小檢驗(yàn)樣本量n, 從而確定模型的Bayes抽樣檢驗(yàn)方案(n,C1,C2). 假設(shè)某種產(chǎn)品的指標(biāo)值為X,且X~N(μ,σ2).根據(jù)歷史數(shù)據(jù)得到,該產(chǎn)品指標(biāo)的總體方差為σ2=16,利用平均指標(biāo)的數(shù)據(jù)求得的期望為E(μ)=350=θ.若生產(chǎn)方和使用方協(xié)商確定產(chǎn)品的規(guī)格下限和規(guī)格上限分別為L=346,U=355.通常,生產(chǎn)方承受最大風(fēng)險(xiǎn)限定值為α=0.05,使用方承受最大風(fēng)險(xiǎn)限定值為β=0.10.則利用Matlab搜尋得到拒絕域W的臨界值為346.7和354.8.故T的拒絕域?yàn)閃=(0,346.7)∪(354.8,+∞),將其代入方程組(2),得: 從而確定最小檢驗(yàn)樣本量為44. 即得到模型的Bayes抽樣檢驗(yàn)方案(44,346.7,354.8).這比經(jīng)典統(tǒng)計(jì)方法確定的最小抽檢驗(yàn)本量68要小得多.并且較之經(jīng)典統(tǒng)計(jì)方法,該方法更加簡便易行. 本文針對(duì)正態(tài)分布型產(chǎn)品的指標(biāo)值為正,且總體方差已知,平均指標(biāo)值為已知常數(shù)的情況,利用最大熵原理確定指標(biāo)值的先驗(yàn)分布,根據(jù)Bayes理論確定可靠性抽樣檢驗(yàn)方案.在求解過程中,運(yùn)用Matlab軟件編程搜索拒絕域的臨界值,并由生產(chǎn)方和使用方的最大承擔(dān)風(fēng)險(xiǎn)確定最小抽樣樣本量.這種確定可靠性鑒定試驗(yàn)方案的方法,對(duì)于正態(tài)型分布產(chǎn)品的雙側(cè)規(guī)格限情況,有較大突破,避免了傳統(tǒng)的經(jīng)典統(tǒng)計(jì)方法的繁瑣計(jì)算.最終得到的最小抽樣檢驗(yàn)量也更加節(jié)約經(jīng)濟(jì),效果很好.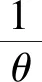
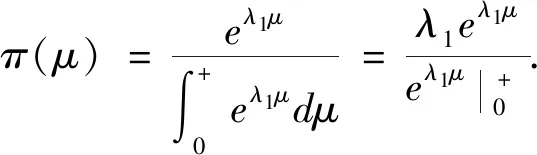
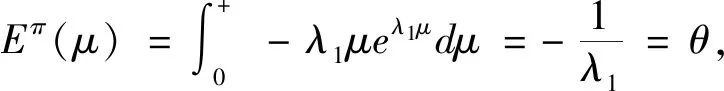
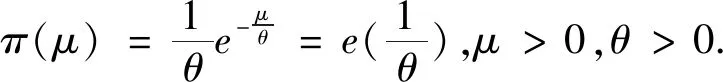
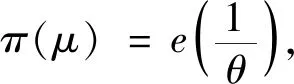
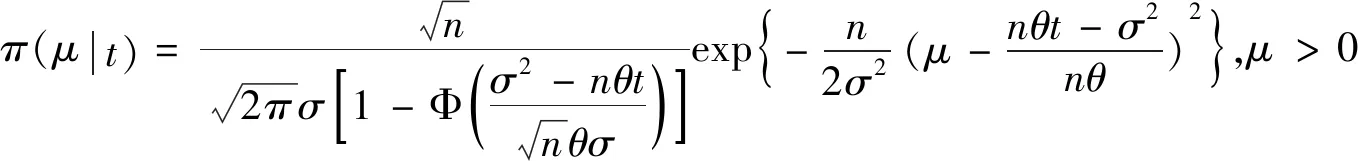
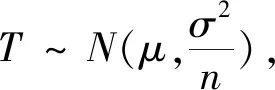
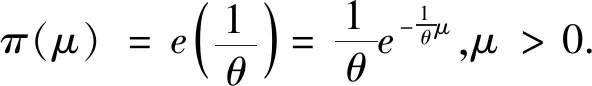
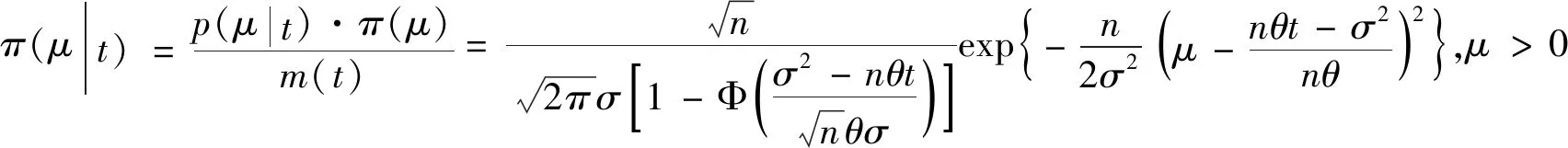
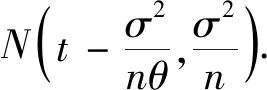

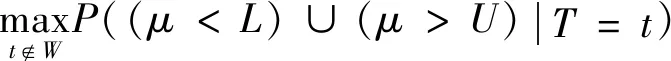
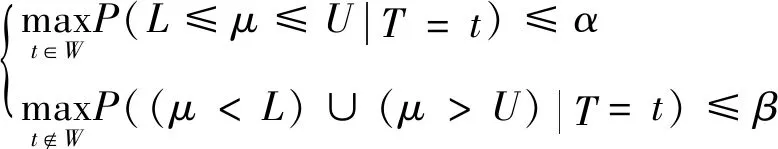
2 模型的求解
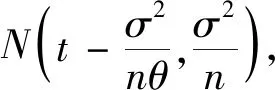
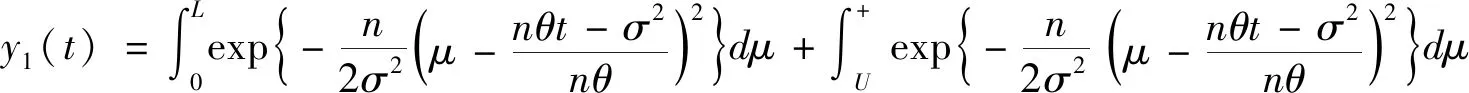
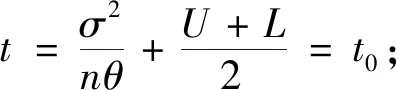
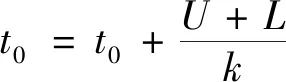
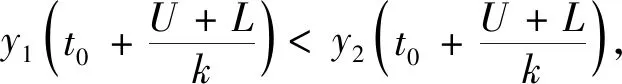
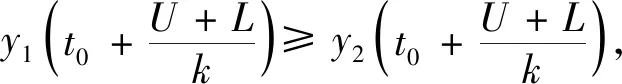
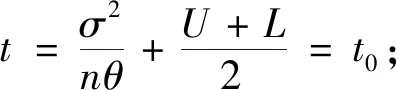
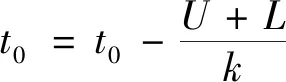
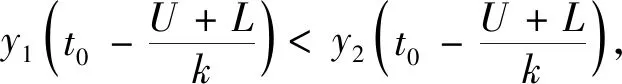
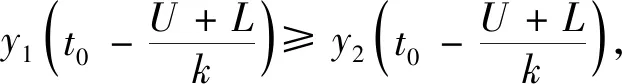
3 算 例
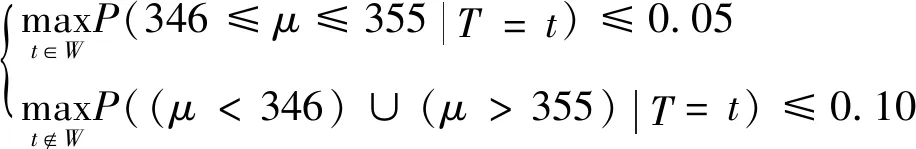
4 結(jié) 論

