波數空間中活塞輻射體近場聲壓分布的計算及測試

衛(wèi)相潤，賀西平，崔曉娟，蒙永紅

(陜西師范大學物理學與信息技術學院，陜西西安710119)

關鍵字：倏逝波；軸向聲壓；圓形活塞

0 引 言

大功率超聲的應用日益廣泛，如：超聲焊接、超聲懸浮、超聲除泡、超聲凝聚、超聲清洗等[1-5]。在超聲應用領域有很多應用活塞式輻射的實例。利用超聲波進行測量、控制、探傷的過程中，圓形活塞式輻射體的應用非常廣泛。因此，研究圓形活塞的振動聲輻射特性具有普遍的意義。

文獻[6]利用疊加法和高斯數值積分算法推導了多階梯圓盤軸向聲壓的分布，計算了軸向聲壓隨距離的變化關系，通過實驗測試得到了軸向輻射聲壓與輸入電功率、圓盤的階梯數目之間的關系。文獻[7]根據點聲源輻射聲場理論，利用點源合成方法推導得到了圓形活塞聲源非均勻振動的輻射聲場分布和指向性函數。

波動現象所引起的振動以及相應的輻射問題，可以用波數空間來描述。通常，這種描述方式對揭示表象下所蘊含的物理意義非常有效。角譜法的基本思想是將波分解成無數個平面波，通過平面波的疊加來計算聲場的傳播[8]。依據角譜法的基本思想，聲場中某一點的聲壓可以唯一且完整地由平面波和倏逝波的疊加來表達。文獻[9-10]中提出了近場聲全息技術，近場聲全息既可以記錄傳播波成分，又可以記錄倏逝波成分。

本文以圓形活塞為例，利用角譜法求得活塞輻射聲場的傳播波和倏逝波的分布。利用數值分析方法[11]，對圓形活塞聲源聲軸線上的聲壓進行計算，得到相應的近場聲壓分布曲線。通過不同聲源半徑、不同輻射頻率下的聲壓分布曲線的比較，得出了近場聲壓的變化規(guī)律。對所設計的階梯圓盤的軸向聲壓進行了測試，實驗測試結果與理論計算結果的趨勢基本吻合。

1 傳播波與倏逝波

超聲速聲波這一概念在1995年由Williams提出[12]。超聲速聲波是指聲波在傳播方向上的相速度比聲速大[13]。波動方程的穩(wěn)態(tài)平面波解由普通的平面波和倏逝波兩部分構成。傳播波的相速度比聲速大，即為超聲速聲波，可以通過普通平面波的疊加而得到，對近場聲壓和遠場聲壓都有貢獻。倏逝波的相速度比聲速小，即為亞聲速聲波，傳播過程中倏逝波的幅值隨距離按指數規(guī)律衰減，因而只對近場聲壓有貢獻。所以在遠場只能檢測到傳播波。

1.1 波數空間

波動現象所引起的振動以及相應的輻射問題，可以用k-空間來描述，這種描述方式對揭示表象下所蘊含的物理意義非常有效。如果我們構造矢量，其中，那么矢量k指向即為平面波的傳播方向，任何平面波的傳播方向都可以由矢量k=kxi+kyj+kzk確定。

因而平面波能夠用如下的更為簡潔的公式ei(kxx+kyy+kzz)=ei(k?r)來表示，其中，r=xi+yj+zk表示聲場中觀測點處的位置矢量，矢量k給出了波的傳播方向。

1.2 傳播波

無源的穩(wěn)態(tài)聲波亥姆霍茲(Helmholtz)方程為

其三維的通解為

滿足：

利用逆傅里葉變換，并且不考慮時間依賴性，可得在頻率ω0下的解為

其中：k為聲波波數，k=2π/λ，λ為聲波的波長，k=ω0/c，c為聲速。

考察y=0時xz平面上的聲壓。令ky=0，，其相位φ為φ=kxx+kyy+kzz-ω0t。其中：x方向的相位為kxx-ω0t，波長λx=2π/kx，相速度cx=ω/kx；z方向的相位為kzz-ω0t，波長λz=2π/kz，相速度cz=ω/kz。

圖1表示xy平面的波數圓，半徑為k，可見傳播波對應的波數分量末端端點落在波數圓內。

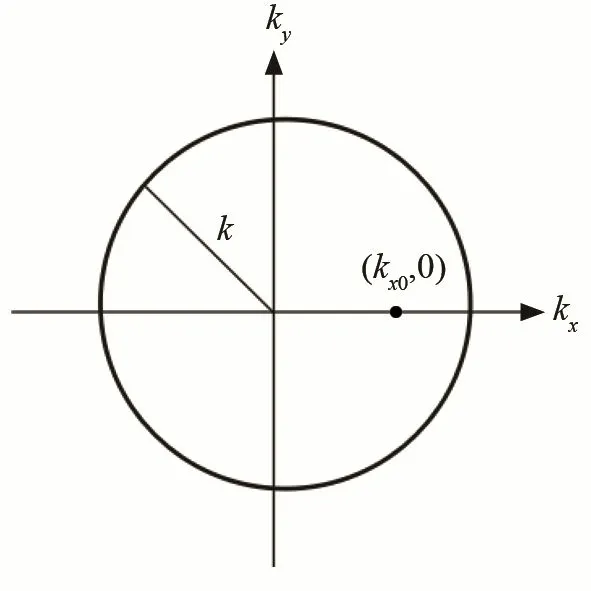
圖1 平面?zhèn)鞑ゲ▽牟〝祱AFig.1 Wavenumber circle corresponding to plane propagation wave

設θ為波的傳播方向與z坐標軸的夾角，由于k=ω/c，kx=ksinθ，kz=kcosθ，則：cx=c/sinθ，cz=c/cosθ，可見，cx、cz均大于聲速c，即為超聲速聲波。

1.3 倏逝波

在式(3)中，kx與ky為獨立的自變量，它們與聲源所在的平面結構有關，分別為波數沿x、y方向上的空間頻率分量。而kz為因變量，其取值依賴于前兩個自變量，它表示聲場中的傳播波成分或倏逝波成分。可以看出，波的傳播性質和傳播方向取決于kx、ky的大小。若，則對應的波即是倏逝波。

kz是虛數，，由式(2)可得：

式(5)可以表示倏逝波的聲壓，聲壓在z方向上的幅值呈指數衰減。同理可知，若cx＜c，即為亞聲速波。圖2表示xy平面的波數圓，半徑為k，可見倏逝波對應的波數分量末端端點落在波數圓外。

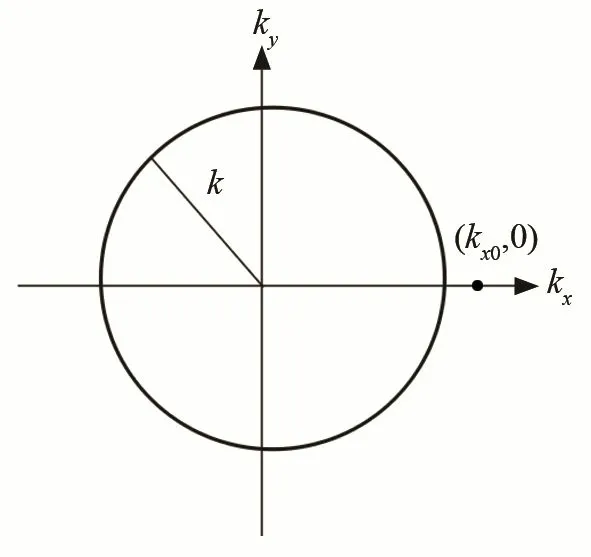
圖2 倏逝波對應的波數圓Fig.2 Wavenumber circle corresponding to evanescent wave

2 角譜法

2.1 角 譜

考察在z＞0的自由半空間中，一個未知的穩(wěn)態(tài)聲壓分布為p(x,y,z)。該聲壓能夠唯一且完整地由具有上述形式的平面波和倏逝波的疊加來表達[14]。構成聲壓的平面波和倏逝波可能有不同的幅值和相位，通過乘以一個依賴于kx與ky兩個波數的系數項p(kx,ky)，希望無源自由場中的任意聲壓分布都可以表達為一組波的疊加，如

式中的指數項作為平面波或者倏逝波。由于x方向與y方向可以無限地延伸，希望波數有連續(xù)性，因而將式(6)的求和式化為連續(xù)積分。于是，聲壓場更具一般性的表達為

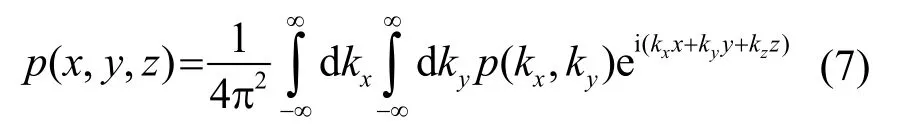
式(7)的包括了從亞聲速波到超聲速波所有波數的取值。討論聲源均被限定在z≤0的空間里(沒有平面波沿著-z軸的方向傳播)的情況，只取正的kz值。在式(7)中，如果z=0，有

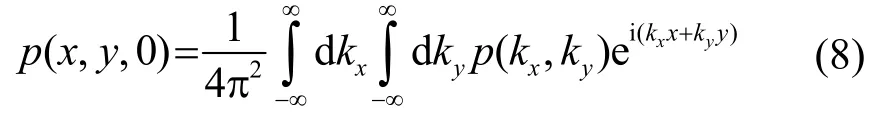
式(8)是無限大平面z=0上的聲壓表達式。該積分式代表了兩個分別關于kx與ky的傅里葉逆變換。復幅值p(kx,ky)的表達式由相應的二維傅里葉變換得出：

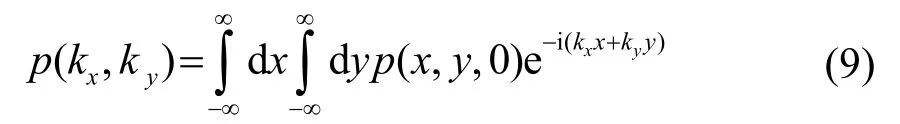
傅里葉變換保證了任意的聲壓分布p(x,y,0)都可以由式(8)表示。p(kx,ky)稱為角譜。角譜法的基本思想就是將波分解成無數個平面波，通過平面波的疊加來計算聲場的傳播。

2.2 角譜法計算圓形活塞聲源近場聲壓

在近場范圍內，聲源在任何平面上的聲場都可以通過平面?zhèn)鞑ゲê唾渴挪ǖ寞B加來得到。

式(7)可進一步表示為

以半徑為r0的圓形活塞為例，設聲源位于z＝0的xy平面上，可以得到z＝0平面上的聲壓p(x,y,0)：

2.3 圓形活塞聲源聲軸線上的聲壓分布曲線

考慮聲軸線上的傳播波和倏逝波的分布，則r=0，空間距離z的變化范圍為0～1 m。此時，式(17)、(18)可寫為

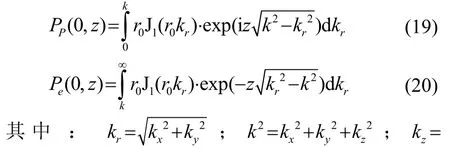
設定圓形活塞聲源半徑r0=35.0 mm，選取共振頻率f=17.1 kHz的聲源，c=340 m·s-1，則可得k=316.7。利用數值積分方法，可得圓形活塞聲源聲軸線上的聲壓分布曲線，如圖3所示。

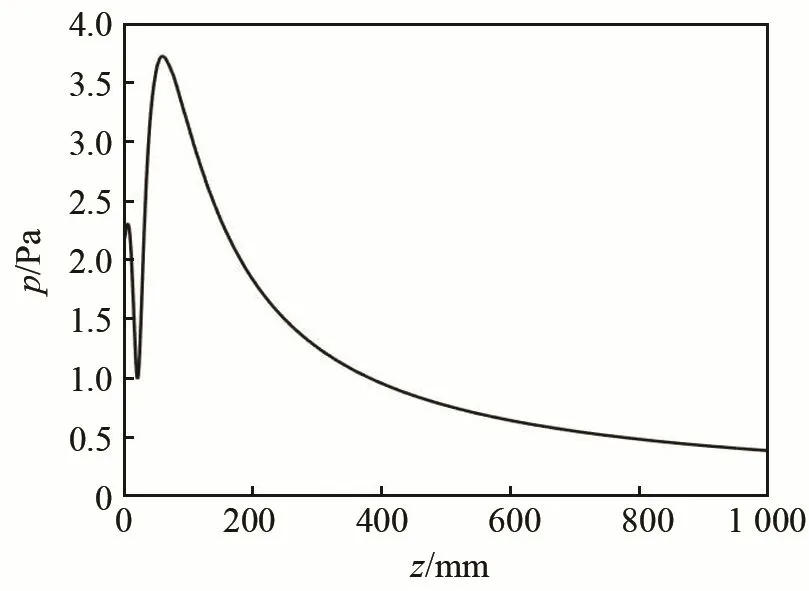
圖3 圓形活塞聲源聲軸線上的聲壓分布曲線Fig.3 The sound pressure distribution curve along the sound axis of circular piston

由圖3可見，在zd=61.0 mm附近圖像出現最后一個極值點，可判定此點即為近遠場的分界點，zd即為圓形活塞聲源的近遠場臨界距離。

2.4 點源組合法計算近場聲壓

以半徑為r0的圓形活塞為例，設活塞速度為u=uaejωt。我們用點源組合法解決該聲源的輻射問題[15]。將聲源劃分成許多微元，微元上所有點源到達待測點時，其振幅相等、相位相同，將所有微元的聲壓貢獻疊加起來可以得到聲源的總聲壓：

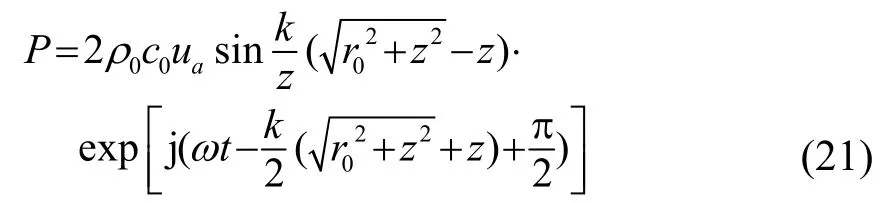
式中：ρ0為聲源靜態(tài)密度；c0為聲速；ua為質點振速幅值，k為波數，r0為圓形活塞半徑，z為待測點離開活塞中心的距離。令：

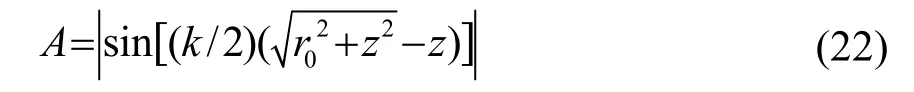
式(22)描述了聲軸線上的聲壓振幅隨距離z而變化的規(guī)律。

將式(22)展開成級數，經計算，當zg=r02/λ時，聲壓振幅為最后一個極大值點，且當zg＞r02/λ時，聲壓振幅隨距離z反比的衰減。最后一個極大值的位置可以看作活塞輻射近場過渡到遠場的分界線，因此zg也可稱為活塞聲源的近遠場臨界距離。以半徑為35.0 mm，共振頻率為17.1 kHz的圓形活塞聲源為例，代入數據計算可得，本算例中：zg=r02/λ=61.8 mm。

由以上分析可知，由角譜法計算得到的聲壓分布曲線中近遠場分界點與點源組合法所得結果一致。

2.5 不同聲源半徑時、不同輻射頻率下聲壓分布曲線的比較

由式(19)、(20)可知，圓形活塞聲源聲軸線上的總聲壓還與聲源半徑r0有關。設定共振頻率不變(20 kHz)，選取半徑不同的聲源可以得到聲場中總聲壓與聲源尺寸的關系，結果如圖4所示。圓形活塞聲源聲軸線上的總聲壓還與聲源的頻率大小有關。設定聲源半徑不變，不同輻射頻率下聲場中總聲壓的變化關系如圖5所示。

從圖4可以看出，聲壓幅值隨著聲源半徑的增大有所增加，近遠場臨界距離隨著聲源半徑的增大而增大。從圖5可以發(fā)現，聲壓幅值隨著輻射頻率的增大有所增加，近遠場臨界距離隨著輻射頻率的增大而增大。

圖4 圓形活塞不同聲源半徑時聲軸線上的聲壓分布曲線Fig.4 The sound pressure distribution curves of circular pistons with different sound source radius

圖5 圓形活塞聲源不同輻射頻率下聲軸線上的聲壓分布曲線Fig.5 The sound pressure distribution curves of circular pistons at different radiation frequencies

3 實驗測試

由于輻射平圓盤的振動節(jié)線兩側相位相反，所以將輻射圓盤表面改進為階梯圓盤，即在平圓盤的節(jié)線上直接豎起階梯，階梯高度為聲波在輻射介質中的1/2波長，這樣可以避免相位相反的相消干涉。文獻[16]提出，階梯盤的輻射理論上應等于對應活塞的輻射，即階梯盤是活塞式輻射器。文獻[17]進一步驗證了這一結論，用解析法計算的指向性圖與其相應的活塞的指向性圖相當。現用階梯圓盤代替圓形活塞進行實驗。

設計了一個45#鋼材的單階梯圓盤，尺寸參數如表1所示。其中f為彎曲振動頻率，h1和h2分別為階梯圓盤的厚度和基底厚度，a和r分別為階梯圓盤的半徑和節(jié)線半徑。材料參數為：材料密度ρ=7.8×103kg·m-3，泊松比σ=0.28，彈性模量E=2.16×1011Pa。

表1 單階梯圓盤的尺寸參數Table 1 Dimension parameter of the stepped circular plate with a single step

實驗測試裝置如圖6所示。將階梯圓盤嵌在大尺寸塑料擋板中，使之與前后方的媒質隔開。超聲波發(fā)生器激勵縱振換能器，階梯圓盤中心與換能器相連，圓盤作彎曲振動。階梯圓盤的中心與麥克風保持在同一高度。前置放大器與麥克風相連的精密噪聲分析儀可以測試所在位置處的聲壓級值。改變麥克風前端與階梯圓盤中心的距離，使之在5.0～1 000 mm間變化(由于測試過程中換能器與階梯圓盤用有一定高度的螺母連接，因而無法從0 mm處開始測量)，并記錄對應位置的聲壓級。將聲壓級換算后得到聲壓的值。

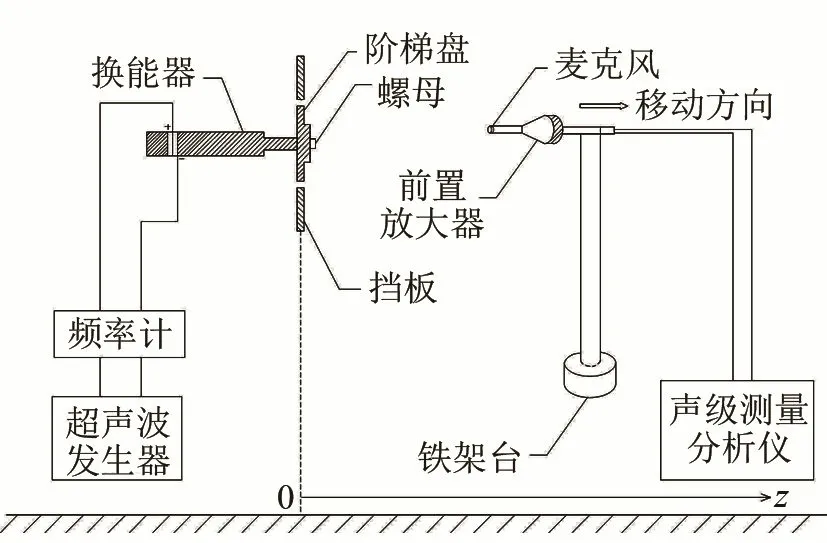
圖6 實驗測試裝置圖Fig.6 Testing apparatus diagram

實驗儀器為精密噪聲分析儀NA-42(測量頻率為1 Hz～100 kHz)，前置放大器NH-5A(靈敏度為0.9 V·Pa-1)，傳聲器uc-29的口徑為1/4in(1in=2.54 cm)、測量頻率為20～100 Hz、靈敏度為0.0042 V·Pa-1)。

階梯圓盤的共振頻率為15.7 kHz，實驗所用換能器的共振頻率為19.8 kHz，復合振動系統(tǒng)的共振頻率為17.1 kHz。按照如上測試方法，經測試可得單階梯圓盤聲軸線上的聲壓分布曲線。利用角譜法結合數值積分方法，與算例對應的圓形活塞聲源半徑為35.0 mm，可得圓形活塞聲軸線上的聲壓分布曲線，如圖7所示。為比較聲場軸向方向上的聲壓隨距離變化的理論計算曲線和實驗測試曲線的趨勢，分別以兩者中的最大值作為分母對兩者的曲線作歸一化處理。從圖7可以看出，實驗測試結果與理論計算結果的趨勢基本吻合。

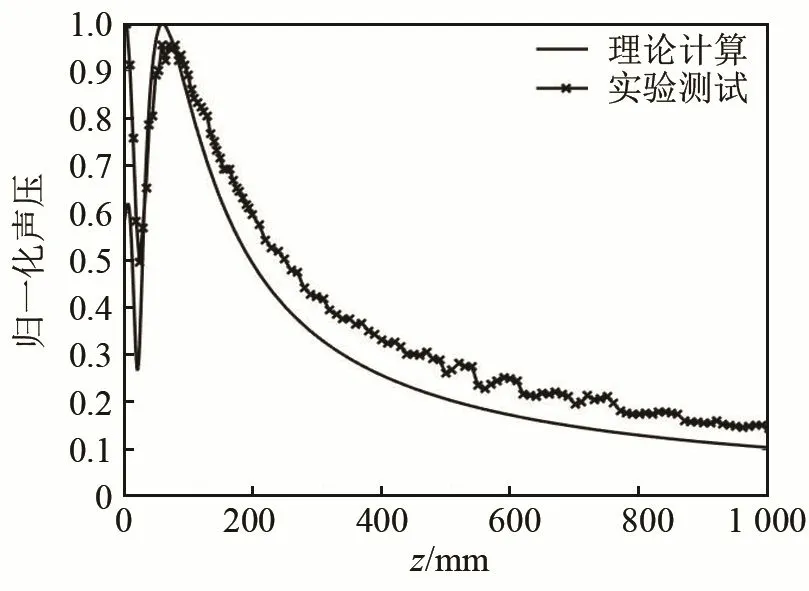
圖7 理論計算與實驗測試對比圖Fig.7 Contrast chart between theoretical calculation and experimental test

4 結 論

利用角譜法可以求得聲源近場范圍內輻射聲場的傳播波和倏逝波的分布，結合數值分析方法，可以得到相應的近場聲壓分布曲線。選定聲源半徑及頻率，經計算得到聲源的聲壓分布曲線，發(fā)現用角譜法與點源組合法計算得到的近遠場分界點一致。通過對不同聲源半徑、不同輻射頻率下的聲壓分布曲線進行比較，可以發(fā)現聲壓幅值隨著聲源半徑的增大有所增加，近遠場臨界距離隨著聲源半徑的增大而增大；聲壓幅值隨著輻射頻率的增大有所增加，近遠場臨界距離隨著輻射頻率的增大而增大。經測試，實驗測試結果與理論計算結果的趨勢基本吻合。