基于二階錐規劃的穩健低旁瓣自適應波束形成
劉 倩,朱安玨
(1.中國科學院聲學研究所東海研究站,上海201815;2.中國科學院大學,北京100049)
0 引 言
在陣列信號處理中,旁瓣級大小一直是波束形成器設計中的一個重要指標。低旁瓣可以有效抑制來自旁瓣區域的干擾,降低目標檢測的虛警概率。目前為止已經出現了大量有關波束旁瓣控制的算法。第一類為加窗法,例如Dolph-Chebyshev加權[1]可以在主瓣寬度一定的情況下獲得最低的均勻旁瓣,但是該方法只適用于均勻線列陣,并且要求各陣元各向同性、不存在差異。第二類為基于自適應陣列理論的方法,例如Olen等在1990年提出的靜態波束圖數字綜合方法[2]。該方法通過在旁瓣區域增加虛擬干擾源,運用自適應陣原理,采用迭代法調節干擾強度從而達到旁瓣控制的目的。該方法適用于任意陣型,并且不要求陣元滿足各向同性,但在迭代過程中會引起波束主瓣的較快增寬并且迭代增益因子難以選擇、迭代存在一定的收斂誤差,導致波束旁瓣不能得到嚴格的控制。第三類為基于凸優化理論的波束圖優化算法,例如Liu等[3]利用二階錐規劃(Second-Order Cone Programming, SOCP)方法設計的旁瓣控制自適應波束形成器,文獻[4-5]提出了基于二階錐規劃的最低旁瓣波束形成器優化設計方法,該類方法適用于任意陣型并且對陣元無要求,可對波束旁瓣進行嚴格控制。
文獻[1-3]中的旁瓣控制波束形成方法只將重點放在了旁瓣級控制方面,而對波束形成器的穩健性沒有提出要求。文獻[4-5]中,通過對加權向量的范數進行約束從而對波束形成器的穩健性進行提升,但在該方法中,加權向量范數的具體約束值通常是根據經驗進行選取,不能通過計算得到嚴格的解。為了使該方法能運用于實際基陣,則需要更進一步提高旁瓣控制波束形成算法的穩健性。眾所周知,自適應波束形成器的性能受到協方差矩陣與期望信號導向向量的影響,當期望信號存在于訓練數據中,并且協方差矩陣估計不準時,自適應波束形成器的性能會出現很大程度的下降。針對以上情況,近年來已有多種改進算法對自適應波束形成器的穩健性進行討論。其中一類是對期望信號導向向量進行估計,例如序列二次規劃(Sequential Quadratic Programming, SQP)算法[6]、最少先驗信息導向向量估計法[7]等。第二類是對協方差矩陣進行改進,其中較為經典的是原始對角加載算法(Load Sample Matrix Inversion, LSMI)[8]及其一系列改進算法,例如加權向量約束法(Norm Constrained Capon Beamforming, NCCB)[9]、最差性能最佳化(Worst-Case Performance Optimization, WCPO)[10]等。但是對角加載類算法在輸入信噪比較高的情況下其輸出信干噪比會出現較大程度的降低,其原因是,此類算法無法去除期望信號存在于訓練數據中所帶來的影響,接收信號中始終包含期望信號成分,當信噪比逐漸增高時,各類誤差所導致的信號“自消”現象始終存在,導致自適應波束形成器產生較大的性能下降,而對角加載類方法無法改進這種性能下降。
本文針對自適應波束形成器的旁瓣控制和穩健性提高方面,提出了一種基于二階錐規劃的穩健低旁瓣自適應波束形成器設計方法,本方法對波束形成器的旁瓣級進行控制,并且利用干擾和噪聲協方差矩陣重構法對波束形成器的穩健性進行提高,從而達到低旁瓣和高穩健性這兩個目的。
1 基于SOCP的圓弧陣波束圖設計
1.1 二階錐規劃簡介
二階錐規劃是凸優化問題的一個子集,常常被用來解決波束優化設計問題。SeDuMi工具箱可專門用于解決二階錐規劃問題,其具有計算量小和計算結果精確的特點,并且可對優化問題的可解與否直接進行判別[11]。在SeDuMi中,標準的對稱錐優化問題形式定義為
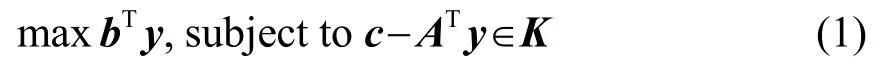
式中:y包含優化變量,A是任意矩陣,b與c是任意向量,K是一個對稱錐集合,零錐與二階錐都是對稱錐的子集。
q維二階錐的定義為
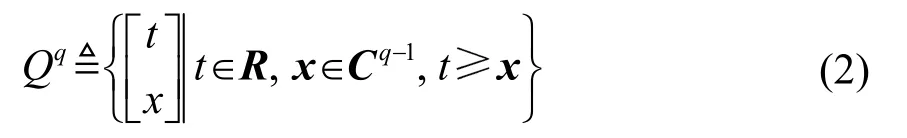
式中:x為所求優化變量,C為復數向量集,t為二階錐的限定范圍。
零錐定義為

式(3)可以代表等式約束。
波束優化設計問題即是將加權向量w的求解轉化為在一系列線性等式與二階錐約束條件下使得目標函數最大化的問題。即將約束問題寫成如下形式:
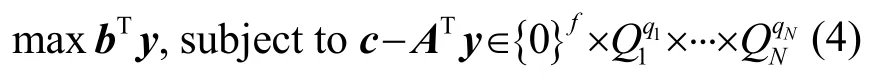
然后再利用已有的內點方法對上述問題進行求解。
1.2 干擾加噪聲協方差矩陣重構
前面已經提到,對角加載類算法雖然可以對自適應波束形成的性能進行改進,但其輸出信干噪比在輸入信噪比較高時還是會出現較大程度的降低。因此,為了提高波束形成器的穩健性,一種有效的方法就是將協方差矩陣中的期望信號成分濾除。基于此思想,Gu等提出了干擾協方差矩陣重構算法[12]。該算法利用Capon空間譜估計,對期望信號存在區域以外的其他區域進行積分,從而獲得重構的干擾加噪聲協方差矩陣,減小了期望信號存在于接收信號中所帶來的干擾。具體步驟如下:
假設觀測區間由Θs與Θi+n兩部分組成,其中Θs為期望信號所存在的區域,Θi+n為干擾信號存在的區域,sΘ與Θi+n互補。利用Capon空間譜估計作為空間譜分布,再對Θi+n區間進行積分則可得到重構的干擾加噪聲協方差矩陣,即:
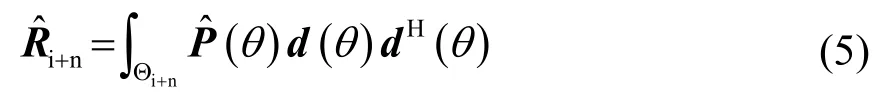
2 基于SOCP的穩健低旁瓣自適應波束形成
假設陣元數為N,波束的主軸方向為θs,旁瓣區域為ΘSL,θj∈ΘSL,則穩健低旁瓣自適應波束形成可以表述成下述問題:
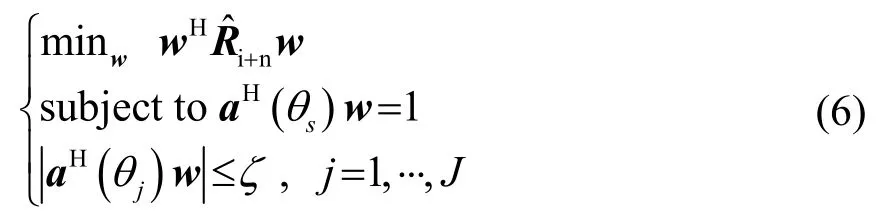
首先,利用楚列斯基(Cholesky)分解將上述問題中的二次目標函數轉換為線性目標函數,即:

引入一個非負標量τ,使得Lw≤τ,則上述問題可以轉化為
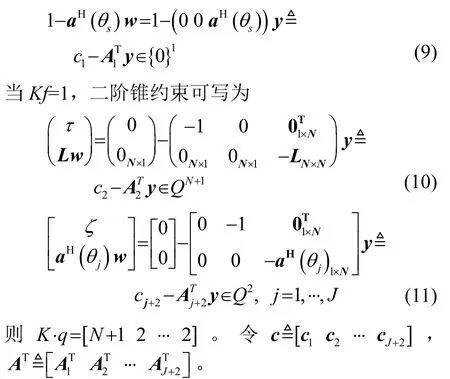
最后,將b、c、AT、K代入SeDuMi中即可求解出y和復加權向量w=[y3y4…yN]。
3 仿真分析
3.1 旁瓣控制性能分析
假設一半徑為0.262 5 m、張角為165°的圓弧上均勻分布著384個陣元,定義圓心為極坐標原點,最中心兩個陣元中垂線所在方向為0°方向。假設信號頻率為390 kHz,選取相對0°方向對稱的186個陣元在0°方向形成波束。在理想情況下,給出圓弧陣常規波束圖和基于二階錐規劃的低旁瓣自適應波束圖,如圖1所示,放大后的波束圖如圖2所示。
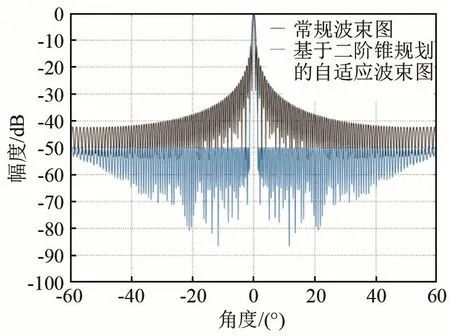
圖1 理想情況下圓弧陣波束圖Fig.1 Arc array beam pattern under ideal condition
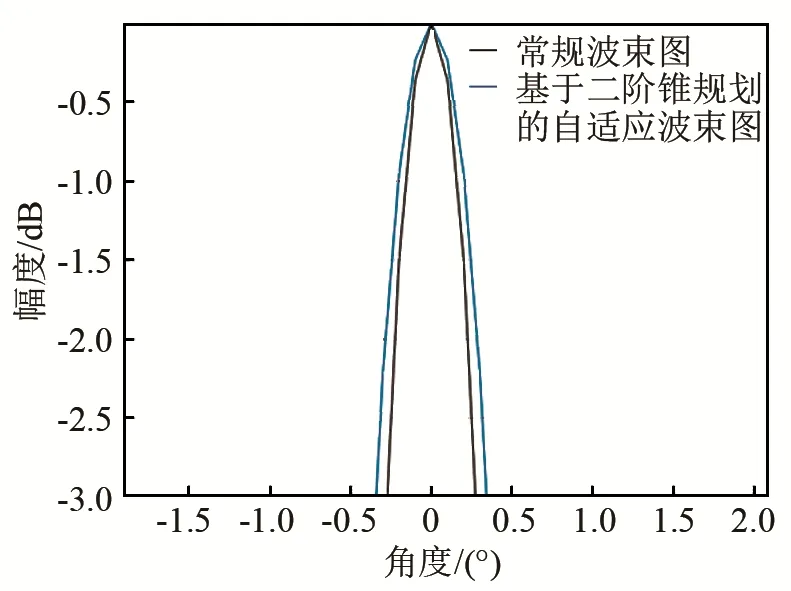
圖2 放大后的波束圖Fig.2 Enlarged beam pattern
由圖1可以看出,圓弧陣的常規波束圖旁瓣較高,最高旁瓣級大約為-11.95 dB,而基于二階錐規劃的低旁瓣自適應波束圖可以將[-60°,-1.5°]∪[1.5°,60°]區域的旁瓣級控制到-50 dB。由圖2可以看出,常規波束形成波束圖-3 dB束寬約為0.55°,而基于二階錐規劃的低旁瓣自適應波束圖-3 dB束寬增大到約0.86°。
3.2 穩健性分析
波束形成器的穩健性是指其在理想情況下獲得的性能指標(如輸出信干噪比)在存在各類失配情況下的下降程度。加權向量范數的大小是表征波束形成器穩健性高低的一個指標,波束加權向量范數越小,波束形成器對誤差的靈敏度越低,穩健性越高。
本文將針對以下兩種常見的失配情況,分別利用對角加載(LSMI)、最差性能最佳化(WCPO)以及協方差矩陣重構法(R-Reconstruction)對樣本協方差矩陣進行改進,計算不同輸入信噪比(Signal to Noise Ratio, SNR)情況下波束形成器的輸出信干噪比(Signal to Interference plus Noise Ratio, SINR)以及加權向量范數的值,并與未進行改進的樣本協方差矩陣求逆法(Sample Matrix Inversion, SMI)的輸出信干噪比進行比較。
3.2.1 陣元位置與響應存在誤差
在實際中,由于人工安裝會導致陣元位置產生一定的誤差,并且陣元會存在一定的方向性,導致方向幅度響應不同,從而給波束形成器的性能帶來一定的影響。考慮陣元位置存在誤差與陣元幅度響應具有一定的方向性的情況,假設上述圓弧陣各陣元真實位置所處角度與理想位置所處角度的誤差服從[-0.05θ,0.05θ]的均勻分布,θ為陣元間隔角度,且各陣元具有方向性,-3 dB響應時的角度為90°。圖3、4所示為陣元位置與幅度響應存在誤差時的波束輸出信干噪比及加權向量范數。
由圖3、4可以看出,在存在陣元位置誤差與響應誤差的情況下,采用干擾協方差矩陣重構法(R-Reconstruction)對樣本協方差矩陣進行改進后,相對于SMI、LSMI與WCPO方法,在輸入信噪比逐漸增大的情況下,輸出信干燥比略高于WCPO,遠高于SMI與LSMI,并且具有最小的加權向量范數值,穩健性最高。
3.2.2 期望信號在傳播過程中產生波前畸變
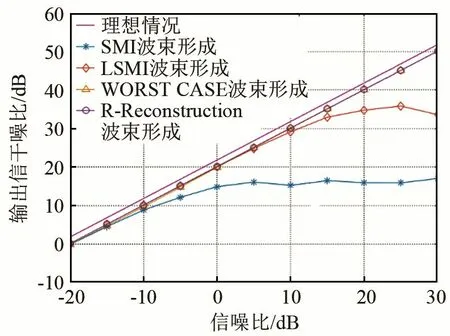
圖3 陣元位置與幅度響應存在誤差時的輸出信干噪比Fig.3 Output SINR when error appears in sensor position and amplitude response
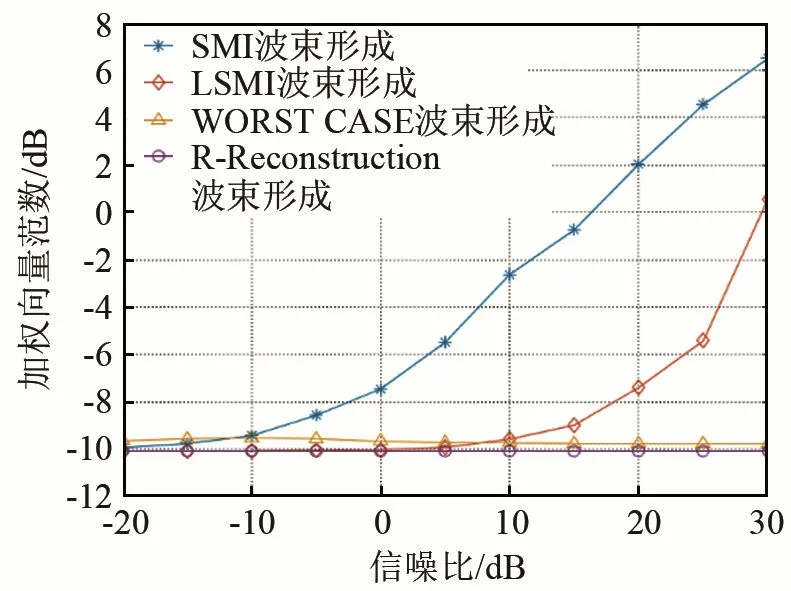
圖4 陣元位置與幅度響應存在誤差時的加權向量范數Fig.4 Norm of weight vector when error appears in sensor position and amplitude response
當期望信號在非各向同性介質中傳播時,非常容易產生一定的幅度和相位的畸變,會導致期望信號導向向量產生一定的誤差,從而波束形成器的性能下降。假設期望信號導向向量在傳播過程中產生了相位畸變,相位誤差服從均值為0、方差為0.04的高斯分布。圖5、6所示為期望信號存在波前畸變時的波束輸出信干噪比及加權向量范數。
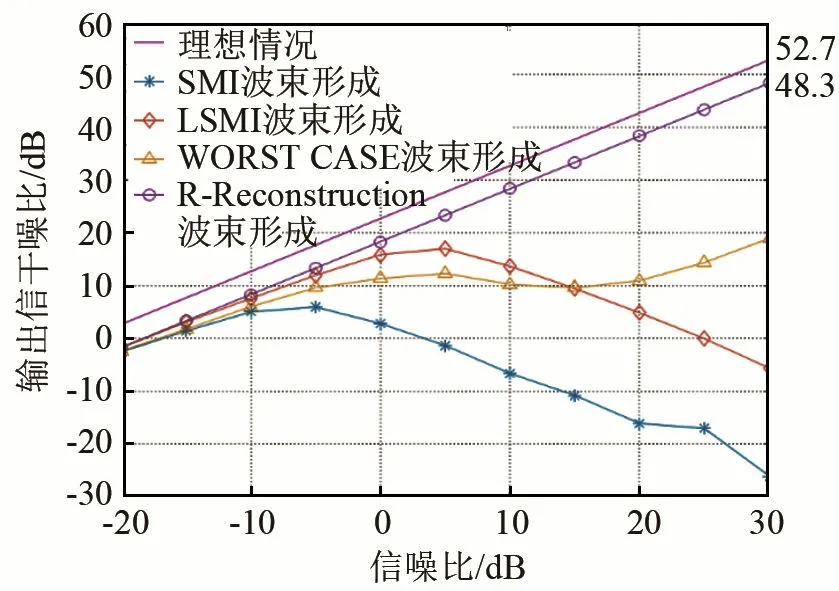
圖5 期望信號存在波前畸變時的輸出信干噪比Fig.5 Output SINR in the case of wavefront distortion
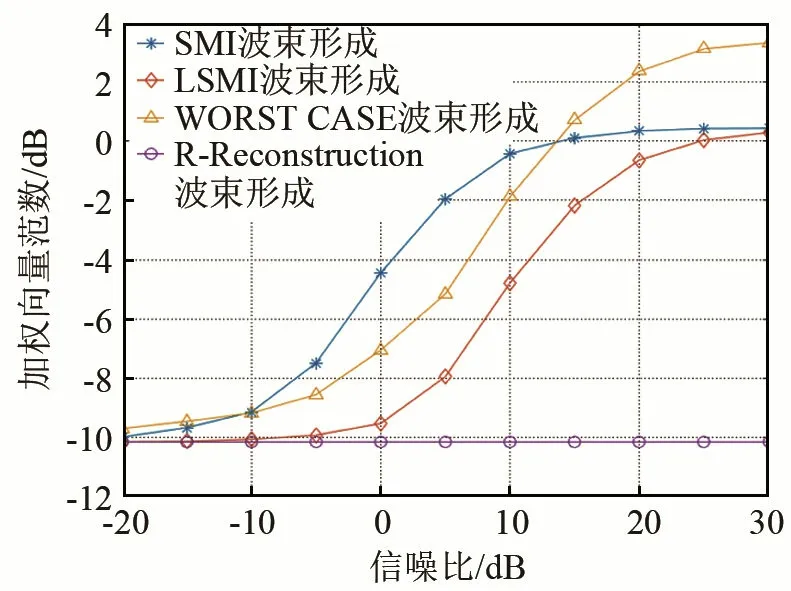
圖6 期望信號存在波前畸變時的加權向量范數Fig.6 Norm of weight vector in the case of wavefront distortion
由圖5、6可以看出,在期望信號存在波前畸變的情況下,在輸入SNR 大于-10 dB之后,SMI、LSMI與WCPO算法的輸出SINR均產生了很大程度的下降,而采用干擾協方差矩陣重構法(R-Reconstruction)對樣本協方差矩陣進行改進后,相對于理想情況下的輸出SINR只下降了約4 dB,性能下降遠小于其他3種算法,并且其具有最小的加權向量范數值,穩健性最高。
綜合上述兩種失配情況下波束形成器的輸出信干噪比和加權向量范數的結果可以看出,利用LSMI、WCPO和R-Reconstruction算法對樣本協方差矩陣進行改進后,波束形成器的輸出SINR相較于未進行改進的SMI算法均產生了較大程度的提高,但利用R-Reconstruction對樣本協方差矩陣進行改進后,相較于利用LSMI與WCPO算法,輸出SINR更高。并且當輸入SNR增大時,輸出SINR與理想情況下的輸出SINR相差都為一定值,而其他方法在輸入SNR逐漸增大的情況下,輸出SINR下降程度越來越大,穩健性更低。
4 實驗結果及分析
為了驗證基于二階錐規劃的穩健低旁瓣自適應波束形成方法對成像效果的改進,進行了水池實驗。首先將成像聲吶放置在水池一側的中間位置,在成像聲吶中心線正前方6.78 m處放置一個點聲源,與成像聲吶同深度。成像聲吶的基陣是具有384個陣元、半徑為0.262 5 m、張角為165°的圓弧陣列,信號頻率為390 kHz。實驗中每186個陣元形成一個波束,共形成了384個波束。采用常規波束形成和基于二階錐規劃的穩健低旁瓣自適應波束形成的結果如圖7所示。圖7(a)為常規波束形成成像結果,7(b)為穩健低旁瓣自適應波束形成成像結果。圖8為某距離處的輸出強度。
從圖7中可以看出,在無強干擾的情況下,利用上述兩種方法均可以分辨出目標的位置。但是常規波束形成成像中目標的旁瓣級較高,在目標檢測時易產生虛警。而本文提出的基于二階錐規劃的穩健低旁瓣自適應波束形成的成像,由于波束旁瓣級大大降低,因此目標變得更清晰,但是波束主瓣增寬,會在一定程度上降低成像聲吶的分辨率。
從圖8中可以看出,在對目標成像強度不變的情況下,本文所提算法可以將旁瓣區域的強度降低約10 dB左右,但并未達到仿真所得到的效果,產生此種情況的原因可能為:(1) 在仿真時對自適應波束形成失配情況考慮不全面;(2) 在協方差矩陣重構時,對于期望信號所存在的區域估計不準,導致在后續的優化計算中,旁瓣區域的設定存在問題,導致優化計算出的解存在誤差。
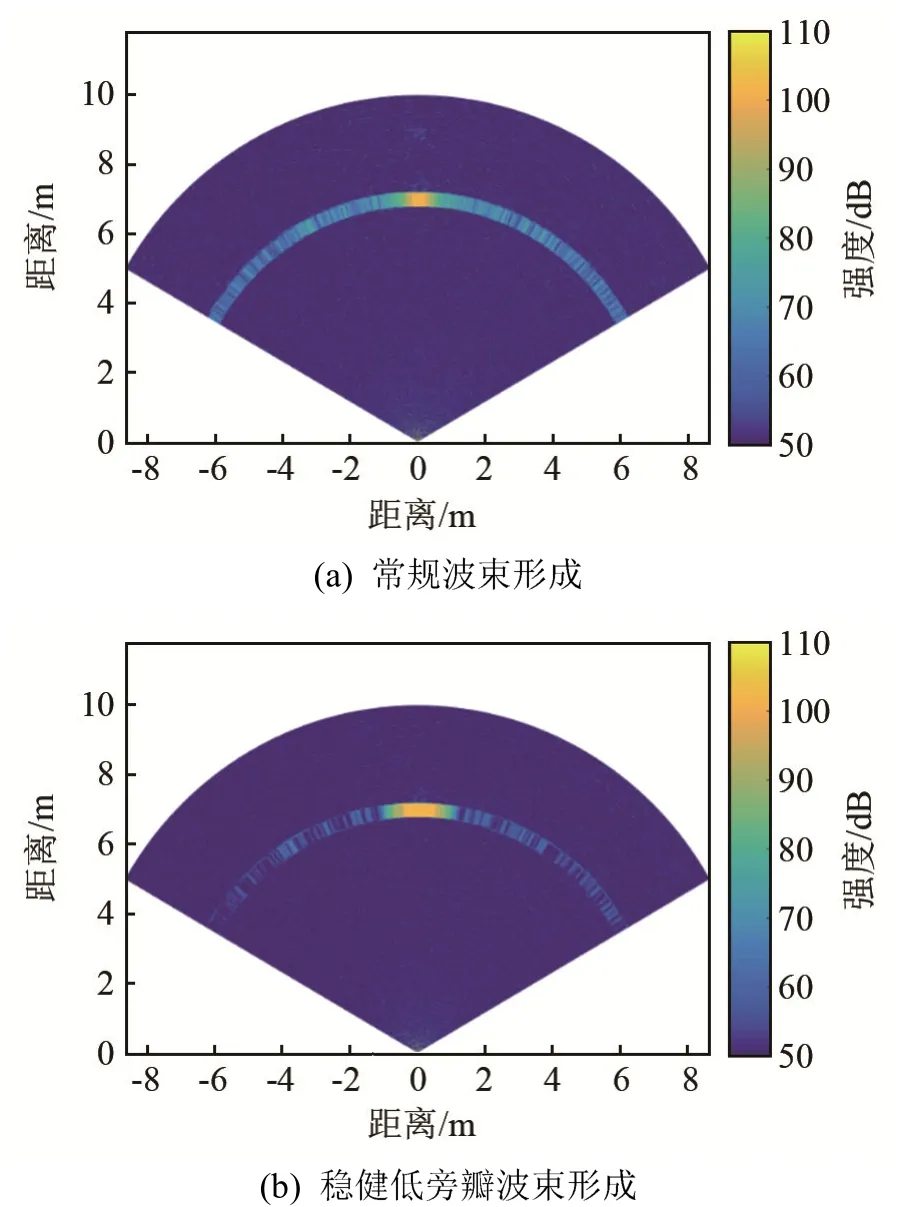
圖7 不同波束形成算法的成像效果Fig.7 The imaging effects of different beamforming methods
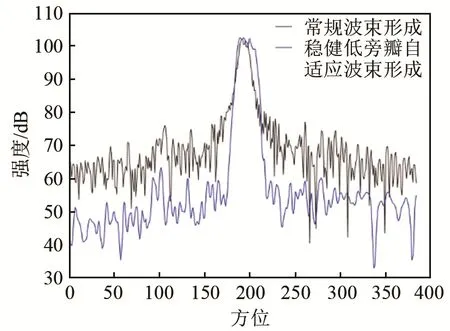
圖8 某距離處的輸出強度Fig.8 Output intensities at a distance
5 結 論
本文提出了一種基于二階錐規劃的穩健低旁瓣自適應波束形成算法,該算法利用二階錐規劃算法設計低旁瓣自適應波束形成,并且針對自適應波束形成容易受到各類失配因素的影響從而導致性能大幅下降的問題,利用干擾加噪聲協方差矩陣重構法對該算法的穩健性進行提高。仿真結果表明,該算法在很大的輸入信噪比范圍內可以獲得接近于理想情況下的輸出信干噪比,并且加權向量范數最小,穩健性最高。水池實驗結果證明,本文所提算法在成像時,可以在一定程度上降低旁瓣級,但是并未達到理論計算值,故本文所提算法還有待改進。

