由《四邊形內角和》證明方法引發的思考

摘 要：數學學科核心素養要求培養學生的創新和實踐能力，《四邊形的內角和》一課中，教師慣用的證明方法就是課本中的分割法，將四邊形分割成三角形，利用三角形的內角和證明，在這個過程中，是否有其他的證明方法，如何充分發揮學生的主觀能動性，值得我們去反思總結，學生想出來的辦法是否嚴謹，值得我們去研究探索。

關鍵詞：四邊形;內角和;證明;轉化

本學期在教授人教版教材八年級上冊《多邊形的內角和》一節的課前備課時，證明四邊形內角和為360°，根據教材，利用分割法將四邊形分割成三角形來證明。四邊形轉化為三角形求內角和，這種辦法對于學生來說易想且簡單，并且有利于幫助學生利用規律求出n邊形內角和，于是我預設了以下幾種學生容易想到的辦法。

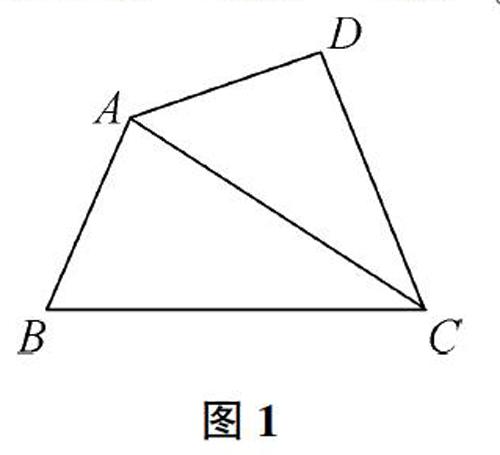
圖1直接連接一條對角線，將四邊形分割成兩個三角形，即180°×2=360°。

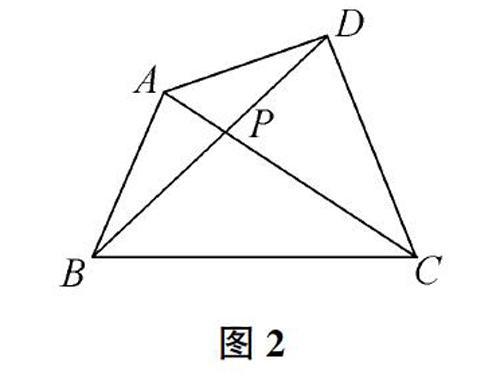
圖2連接兩條對角線AC、BD，形成四個三角形，四邊形內角和相當于4個三角形內角和減去周角360°，4×140°-360°=360°。

這四種方法中，圖1和圖2是絕大部分學生能夠想到的辦法，對于少部分學生來講，圖3與圖4就需要教師的引導。

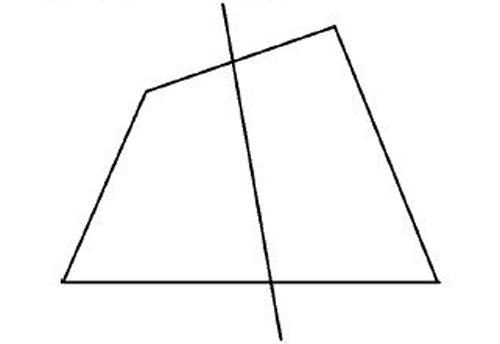
老師會提問，圖2中的點P是兩條對角線的交點，比較特殊，如果點P沒有這么特殊，你還能將四邊形分割成三角形嗎？

學生經過教師的引導，可以得出圖3的方法，教師再提問，點P還能取在其他地方嗎？點P能取在四邊形的邊上嗎？學生可能會得出圖4。總結得出P點可以取在四邊形內部，也可取在四邊形的邊上，當點P取在對角線交點處，其實就是特殊的圖1。

教學這節課時，老師都會探究這幾種方法，以上幾種方法可以類比到其他的多邊形中，很多時候，我為了教授完課堂教學的內容，放棄了讓學生深入挖掘的想法，從而扼殺了學生思維的創造性和發散性，這并不是真正的數學教學。于是這次我在備課的時候，準備讓學生暢所欲言，給他們時間，讓他們思維在探索的世界里遨游。

如備課時的預設情景一樣，在實際的教學過程中，學生很順利的得出上面四種方法。

老師再提問：點P除了取在四邊形內部以及邊上，還能取在其他地方嗎？

學生們興趣一下就提高了，他們很快就得出了點P取在四邊形外的情形。

學生們在四邊形ABCD外取一點P，連接PA、PB、PC、PD，四邊形ABCD的內角和等于三個三角形內角和的和減去180°，即180°×3-180°=360°。

到了這里，學生的積極性就被調動起來了，任教的兩個班級想了很多方法。

有同學就想出了這樣一種辦法，他將四邊形分割成了三個直角三角形和一個長方形。

老師：同學們，這種方法成立嗎？

學生經過計算，四邊形的內角和可以是三個三角形的內角和加上4個直角的度數，減去多余的三個平角。

老師給予答案的肯定，再提問，所有的四邊形都可以這樣做輔助線嗎？如果它本身是一個長方形呢？還能這樣做嗎？

學生：不能

老師：那這種方法可以用來證明四邊形內角和嗎？

學生現在就開始產生意見的分歧，經過討論，他們一致認為可以，但是要分類，可以分為特殊的四邊形和一般的四邊形討論。

老師：那我們之前的幾種方法需要分類嗎？

學生：不需要，因為所有的四邊形都可以通過連接分割成三角形，圖1～圖4的方法適合于一切四邊形。

看著同學們在矛盾中頓悟出來的想法，我感到無比的愉悅。這正是這節課的目的所在。

學生又提出，這個圖形太特殊，可以不用作水平和豎直的線，他們又畫出以下圖形：

學生列式3×180°+360°-180°=360°

學生：可以三個三角形的內角和加上中間四邊形360°，再減去多出來的3個平角。

老師：這個方法對嗎？

學生A：不對，我們的目的就是為了證明四邊形的內角和360°，這里直接使用了。

老師對回答給予肯定，并對以上兩種分法進行了區別分析。

老師：還有的別的方法可以證明嗎？上一節課我們是怎么證明三角形內角和的？

學生回憶通過做平行線。

老師：那四邊形內角和能不能作平行線證明了？同學們下課后去思考一下還有沒有其他方法。

到這里下課鈴聲響起了，我不得不停下本堂課的繼續深入了，但是下課不代表停止思考，我把剩下的思考空間作為課后作業留給了學生，讓他們繼續拓展，以實現學生方法和思維的延伸。

兩天以后的一節練習課，專門就學生找到的方法進行了討論。

學生A：我最開始嘗試做BD的平行線AE，并延長BA，

∵∠B=∠FAE，∠D=∠CEA，

∴∠BAC+∠B+∠C+∠D

=∠BAC+∠FAC+∠CAE+∠C+∠CEA

=180°+180°

=360°

在此處鍵入公式。

老師：同學們她證得對嗎？

基本上所有學生認為這種證明方法沒有問題，是對的，并且還有同學提出，他這樣畫輔助線麻煩了，不需要延長BA，只需做出BD的平行線AE，此時四邊形的內角和就等于兩組同旁內角360°，再加上一個三角形的內角和180°，減去多算的一組鄰補角之和180°即可，都得到了學生的認可。

但是在我刻意有疑問的目光中，同學們逐漸感覺出不對了。

學生B發現了：我認為這種證法不完整，也應該像上一節課有種方法一樣分類證明，是不是所有的四邊形都能做出其中一邊的平行線呢，如果四邊形本身有一組對邊或兩組對邊都平行的話就不需要做輔助線，直接利用平行線的性質，同旁內角互補可證。所以如果要用這種方法，那就要幾種情況討論，要分類，要嚴謹。

其他同學這才恍然大悟。

雖然發現這點的同學不多，但是哪怕只有一位學生從之前的證明中已經得到反思，并且應用了起來，也是教學的一種進步，他們已經意識到了數學的嚴謹性。

所以在后面學生C提出了可以過不同頂點做同一條邊的兩條平行線的方法時，他自動參照了同學B的回答，將他的證明步驟完善了。

大家經過又一輪的討論，又得出其他幾種平行線的做法，在這就不一一贅述了。

學生：方程思想行不行？

設四邊形內角和為x，大四邊形的內角和就等于兩個小四邊形的內角和減去兩個平角，可以列一個方程x=2x-2×180°，解得x=360°。

此時，我覺得我的內心是比較激動的，以前確實沒有想過用方程去證明，但仔細一想，這個方法不對，它的前提建立在四邊形內角和都相等的基礎上，學生忽略了這一點，這一點也是以后幾何證明中經常犯的問題，此時正是一次好的教育機會。

老師：你們覺得可行嗎？

這次全班是一致的同意意見，對的。

我注視著他們然后微笑，學生們很了解，當老師出現了這副神態的時候，肯定有問題了。

于是他們開始一步步排查，得出的結論還是沒錯。滿臉好奇的樣子！

老師：我們證明的是什么？

學生：四邊形內角和360°。

老師：方程中用到了三個四邊形，我們都沒有證明出四邊形內角和360°，你怎么知道它們的內角和是相等的，證明能都設為x？

學生們恍然大悟。

老師最后提出問題：這些證明方法的方法，能用來證明五邊形，六邊形、n邊形的內角和嗎？通過我們對四邊形內角和的探索，你有哪些收獲呢？

課后，我調查了學生們對本節課的想法，學生們普遍的想法是從來沒有覺得四邊形的證明方法有這么多，自己能想出一種不同的方法很有成就感，也從其他同學不完整以及錯誤的證法中，得到一些啟發，學會思辨，體會數學的嚴謹。

當然四邊形的內角和證明方法肯定還有許多，這些就等待我們在以后的教學中再繼續引導學生去挖掘。數學是嚴謹的，是發散的，是有趣的。數學核心素養要求教師在教學過程中培養學生的學習能力，這樣的課堂，幫助培養學生的發散性思維，實際上也是在培養學生的創新精神和實踐能力，也是給學生們提供了更廣泛的思維空間，讓他們在多角度，多側面，多途徑的思考中，篩選出最佳的解法，這些都是作為教師的我們應該做的，在新課標要求下，教師不應該一味的照本宣科，應該改革創新，及時反思，并且不斷改進，只有這樣才能培養出具有獨立思辨能力的未來人。

作者簡介：

唐穎，重慶市，重慶市人和中學。