求解不確定型車輛路徑問題的弱魯棒優(yōu)化方法

孫 亮，王 冰，郭 棟，徐 藝

(1. 山東理工大學 交通與車輛工程學院， 山東 淄博 255049；2. 上海大學 機電工程與自動化學院， 上海 200072)

開放式車輛路徑問題(Open Vehicle Routing Problem，OVRP)指企業(yè)租用車輛來完成針對客戶的配送任務，在滿足一定約束條件下確定相應的車輛行駛路線以有序服務客戶，實現(xiàn)決策目標最優(yōu)化。企業(yè)所租用車輛從企業(yè)出發(fā)，完成配送任務后，不必返回企業(yè)。

從物流配送的實際營運過程看，影響第三方物流模式營運效果的因素主要有兩個：①旅行時間的不確定性；②客戶期望的服務時間段。因此，針對不確定型OVRP優(yōu)化方法的研究，對于提升不確定環(huán)境下第三方物流模式營運效果具有重要的理論和現(xiàn)實意義。

魯棒優(yōu)化方法[1]采用不確定數(shù)據(jù)的邊界特性描述模型參數(shù)的不確定性，有效避免了隨機優(yōu)化方法在闡述參數(shù)不確定性上過度依賴先驗知識及服從概率分布假定的弊端。

目前，求解不確定型車輛路徑問題(Vehicle Routing Problem, VRP)的魯棒優(yōu)化方法主要包含兩類：

1)最壞場景魯棒優(yōu)化方法：該方法利用不確定集的邊界值，將不確定的優(yōu)化模型轉(zhuǎn)化為確定的線性規(guī)劃模型，發(fā)現(xiàn)一個對所有觀測值可行的最優(yōu)解，并確保最壞實現(xiàn)下的最優(yōu)目標函數(shù)值達到最優(yōu)。Sungur等提出了需求不確定的VRP的最壞場景魯棒優(yōu)化模型，給出了三種需求限制約束的魯棒對應式[2]。Hu等提出了描述需求和旅行時間不確定VRP特征的魯棒優(yōu)化模型，并分別使用變鄰域搜索方法和分支定界法對各自提出的模型進行求解[3]。Agra等針對旅行時間不確定的VRP，提出此類問題的魯棒優(yōu)化模型[4]。劉洋等以總服務成本最小化為優(yōu)化目標，建立了路徑規(guī)劃問題的魯棒優(yōu)化模型[5]。Cao等提出針對需求不確定的OVRP的魯棒優(yōu)化模型，使用禁忌算法對該模型進行求解[6]。

2) 弱魯棒優(yōu)化方法：該方法是以最小的約束違背來保證目標函數(shù)值始終不超過合理范圍，從而改善最壞值與預期值之間的偏差[7]。Han等提出了基于情景描述旅行時間不確定性的VRP的弱魯棒優(yōu)化模型[8-9]。Wu等針對旅行時間不確定的VRP, 提出了一個抑制目標函數(shù)惡化程度的弱魯棒優(yōu)化模型[10]。

本文以旅行時間不確定的開放式車輛路徑問題(Open Vehicle Routing Problems with Uncertain Travel time,OVRP-UT)為研究對象，提出一個描述該問題特征的弱魯棒優(yōu)化模型。為了進一步提高啟發(fā)式算法獲取最優(yōu)解的概率，在超啟發(fā)式算法的框架下，通過引入預測適應度函數(shù)，提出一種自設計遺傳算法對弱魯棒優(yōu)化模型進行求解。

1 OVRP-UT的弱魯棒優(yōu)化模型

1.1 基本定義

定義1懲罰成本：如果配送車輛完成時間超過客戶允許的最晚完成時間，根據(jù)合同向客戶支付的罰金稱為懲罰成本。

定義2違約車輛：產(chǎn)生懲罰成本的車輛稱為違約車輛。

定義3關于旅行時間的不確定集

定義4極點：?x∈UT,對于?δ>0，x+δ?UT，則稱x是UT的極點。

定義5極點集:UT中由極點構成的子集，用ext(UT)表示。

定義6最壞實現(xiàn)：ext(UT)中極點對應的模型參數(shù)的觀測值稱為最壞實現(xiàn)。

1.2 問題描述

一個完全的賦權圖G=(V,E)，這里V={0,1,2,…,n}為點集，0表示車場，C={1,2,…,n}表示客戶集，客戶的數(shù)量為n；E={(i,j)|i,j∈V,i≠j}為邊集。每一條邊賦有一個旅行時間，旅行時間在UT內(nèi)任意取值。所有車輛具有相同的最大負載Q。每一個客戶i賦有一個需求di，di≤Q。企業(yè)共租用m輛車來完成配送任務，令M={1,…,m}。Bf是配送任務最晚完成時間，如果配送任務完成時間超過Bf，則會產(chǎn)生懲罰成本。ω1表示單位懲罰成本。

對于UT內(nèi)的任意實現(xiàn)，該問題的優(yōu)化目標是為每輛車確定合理的運輸路線，使違約車輛數(shù)和總懲罰成本的加權和達到最小。調(diào)度方案必須滿足以下約束條件：

1)調(diào)度方案對UT內(nèi)的任意實現(xiàn)均保持可行；

2)車輛路線始于企業(yè)，終止于某個客戶，服務完成后，車輛不再返回企業(yè)；

3)客戶點需求必須且只能由一輛車來服務完成；

4)每一條車輛路線上客戶點的需求量之和不超過Q。

1.3 問題建模

1.3.1 決策變量

sik:第k輛車到達客戶i的時刻。

1.3.2 弱魯棒優(yōu)化模型

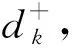
(1)

s.t.

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

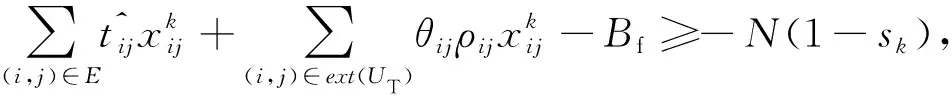
(10)

(11)

(12)

sik≥0,?i∈N,?k∈M

(13)

(14)

(15)

sk∈{0,1},?k∈M

(16)

根據(jù)文獻[8]的定義給出另一類弱魯棒優(yōu)化模型LRO1如下：

約束條件與NLRO相同。

LRO1的特點在于通過控制違約車輛數(shù)，間接實現(xiàn)對總懲罰成本的控制。 不難看出，LRO1是NLRO在ε=0時的特殊情形。

1.4 NLRO的性質(zhì)分析

性質(zhì)1ZNLRO表示NLRO的最優(yōu)解對應的總懲罰成本，ZLRO1表示LRO1的最優(yōu)解對應的總懲罰成本，ZNLRO≤ZLRO1。

由于

所以

則ZNLRO≤ZLRO1。

□

2 求解方法

自設計遺傳算法(Automatic design of Genetic Algorithms， AGA)分為兩部分：①根據(jù)預期適應度函數(shù)值最小的原則，篩選出有利于問題求解的遺傳算法的要素；根據(jù)適應度函數(shù)值最小的原則，篩選出包含當前算法優(yōu)化解的種群。②將兩者組合為一個新的遺傳算法，繼續(xù)對問題進行求解，輸出最終算法優(yōu)化解。

AGA的算法流程如圖1所示。

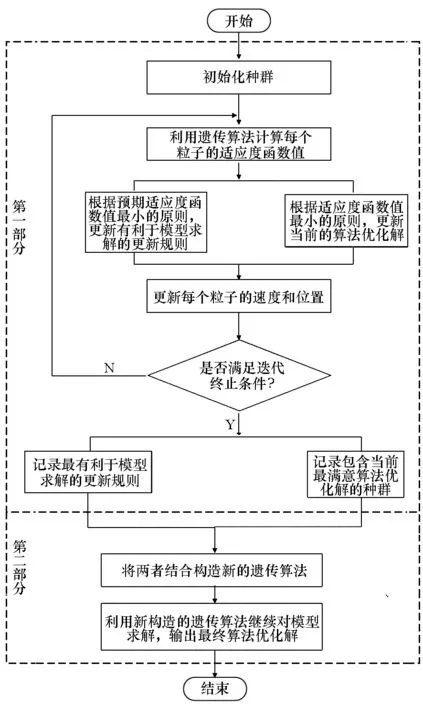
圖1 AGA流程圖Fig.1 Flow chart of AGA

2.1 遺傳算法的關鍵要素

1)染色體編碼方式：染色體共由兩部分組成，第一部分采用基于客戶的編碼方式表示具體的調(diào)度方案，第二部分記錄該調(diào)度方案的適應度函數(shù)值。染色體編碼結構如圖2所示。

圖2 遺傳算法染色體編碼結構示意Fig.2 Chromosome representation of genetic algorithm

2)染色體解碼的具體過程如下：隨機生成新序列{i1,…,in}，依次將該序列中的客戶分配給第1輛車，直到第1輛車的剩余負載無法再為其他客戶服務。重復上述過程，直到所有客戶都能夠被車輛服務。

3)適應度函數(shù)的選取：目標函數(shù)(1)作為染色體的適應度函數(shù)。

2.2 粒子群算法的關鍵要素

2.2.1 粒子的編碼與解碼方法

粒子向量由位置向量、速度向量、適應度函數(shù)值三部分組成。

1)位置向量：構造1×8維向量X，第1維表示選擇因子集合S中的操作類型，第2維表示交叉因子集合Cr中的操作類型，第3維表示變異因子集合Mu中的操作類型，第4維表示遺傳算法的種群規(guī)模Mga，第5維表示遺傳算法的迭代次數(shù)Tga，第6維表示選擇操作選中的個體數(shù)ik，第7維表示交叉概率pc，第8維表示變異概率pm。遺傳算子集合及其構成詳見表1。

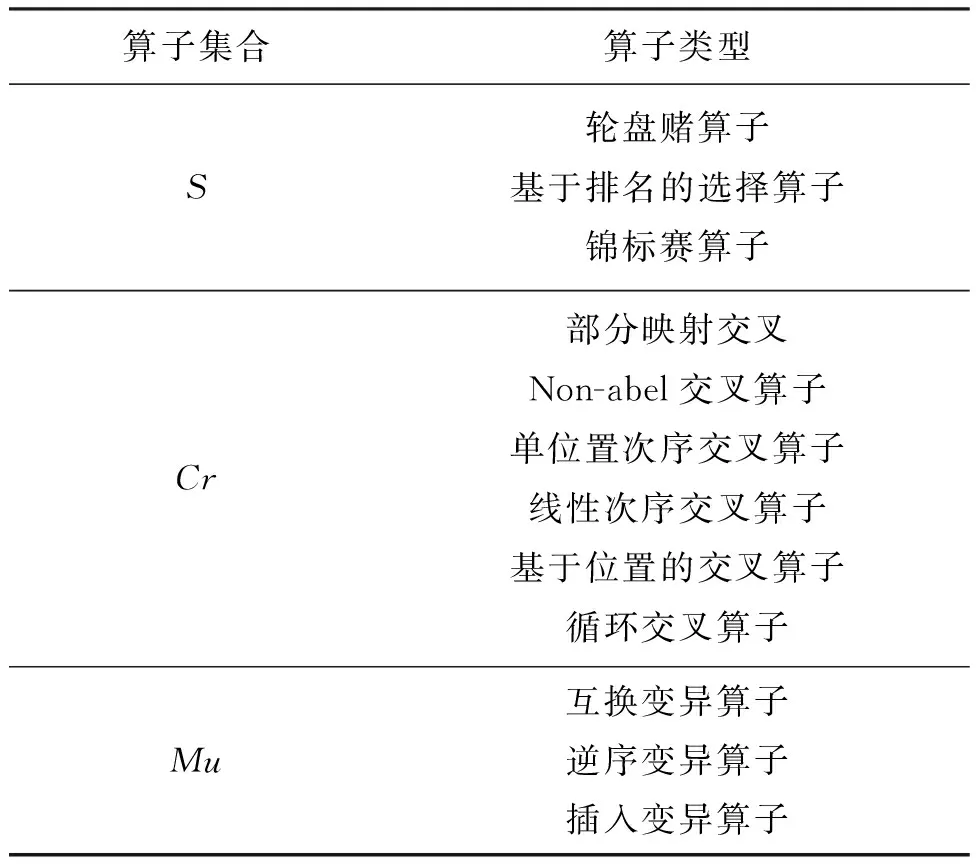
表1 遺傳算子集合及其構成

注：不同算子的操作步驟，詳見文獻[12]。

2)速度向量：速度向量也是一個1×8維向量，用V表示，微粒的運行速度限定在[Vmin,Vmax]。

令

(17)

式中，x0(i)表示該粒子構造的遺傳算法的第i次迭代得到的最優(yōu)適應度函數(shù)值。 令x0={x0(1),…,x0(q)}，對其做一次累加生成運算，即

令

Y=(x0(2)x0(3) …x0(q))T

則a,b可采用下式計算：

(18)

粒子的編碼結構如圖3所示。

圖3 粒子編碼結構示意Fig.3 Particle representation

2.2.2 更新規(guī)則

速度和位置更新公式為：

i=1,2,3,4,5,6,7,8

(19)

i=1,2,3

(20)

Xi(t)=ceil(Xi(t-1)+Vi(t)),i=4,5,6

(21)

(22)

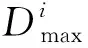
(23)

其中，ω0為慣性因子的初始值，ωe為慣性因子的最終值，T表示粒子群算法迭代的最大次數(shù)；r1和r2為(0，1)之間的隨機數(shù)；a1和a2表示加速因子。

2.3 AGA的算法步驟

AGA的偽代碼如算法1所示。

算法1 AGA的偽代碼

注：①以粒子的位置向量表示的遺傳算法參數(shù)作為輸入，采用標準遺傳算法[12]作為該粒子的解碼算法。

2.4 AGA的性質(zhì)分析

性質(zhì)2令P(Am)表示第m個粒子所構造的遺傳算法能夠在有限時間內(nèi)發(fā)現(xiàn)模型最優(yōu)解的概率，P(Anew)表示新生成遺傳算法在有限時間內(nèi)能夠發(fā)現(xiàn)模型最優(yōu)解的概率，

表示AGA發(fā)現(xiàn)最優(yōu)解的概率事件，則AGA發(fā)現(xiàn)NLRO的最優(yōu)解的概率滿足如下性質(zhì)：

P(B)>max{A1,…,AM·T,Anew}

證明：粒子群算法的搜索過程具有隱含并行性，不同粒子的解碼過程彼此之間不互相影響，因此，Am和Aj是相互獨立的。令P(Ai)=ri,i=1,…,M·T+1，AGA發(fā)現(xiàn)最優(yōu)解的概率為：

又

ri=1-(1-ri)

顯然

所以

從而，命題成立。

□

性質(zhì)3AGA最壞情況下的時間復雜度與遺傳算法的時間復雜度相同。

□

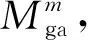
性質(zhì)4AGA最壞情況下的空間復雜度為O(18M+L)。

證明：就空間復雜度而言，每個粒子需要18個變量空間進行存儲，另計算適應度函數(shù)值需要L個輔助變量空間，從算法1看，AGA存儲粒子和生成適應度函數(shù)值是重復利用的，因此AGA的空間復雜度為O(18M+L)。

□

3 仿真分析

3.1 仿真環(huán)境與參數(shù)設置

3.1.1 算例選取與基本參數(shù)設置

在對NLRO和LRO1的優(yōu)化解進行分析時，通常可以借助文獻[13]的標準測試數(shù)據(jù)(C1～C14,O1～O8,vrpnc1～vrpnc14,F11,F12)。此外，還可利用文獻[14]的標準測試數(shù)據(jù) (A-n34-k5，B-n34-k5)分析不確定參數(shù)對NLRO最優(yōu)解的影響。NLRO和LRO1中確定型參數(shù)的取值與標準測試數(shù)據(jù)中的對應取值相同。令ω1=1,ε=1,θij=3,ρij=1,Λ=225,算法參數(shù)信息詳見表2。

表2 算法參數(shù)設置

遺傳算法初始種群的生成方式：首先，隨機生成一組滿足約束(2)～(8)的調(diào)度方案，并記錄該組可行解的每一輛車對應的最大配送完成時間Maxroutetimek。其中，Bf采用如下方式生成：

(24)

然后，根據(jù)Bf的值，隨機生成滿足約束(2)～(16)的調(diào)度方案，并作為遺傳算法的初始種群。

3.1.2 測試環(huán)境

用MATLAB R2016a 64位實現(xiàn)了求解NLRO和LRO1的AGA，在 Intel(R) Core(TM) i5-6200U CPU @ 2.3 GHz，8 GB內(nèi)存的計算機上進行了仿真實驗。

3.2 算法優(yōu)化解的性能分析

針對表2中的模型與算法參數(shù)信息，根據(jù)表3和表4中的Bf，使用AGA對模型NLRO和LRO1分別獨立求解30次，分別取其中的最好解作為各自的算法優(yōu)化解，該解對應的違約車輛數(shù)記錄在表3和表4中的veh_n和veh_nl，總懲罰成本分別記錄在fc_n和fc_nl這兩列中。每一次的運算時間上限設定為3600 s。表3和表4中，cum列表示測試數(shù)據(jù)的客戶數(shù)，problem列表示測試數(shù)據(jù)的名稱。

表3 C類和O類問題優(yōu)化性能分析

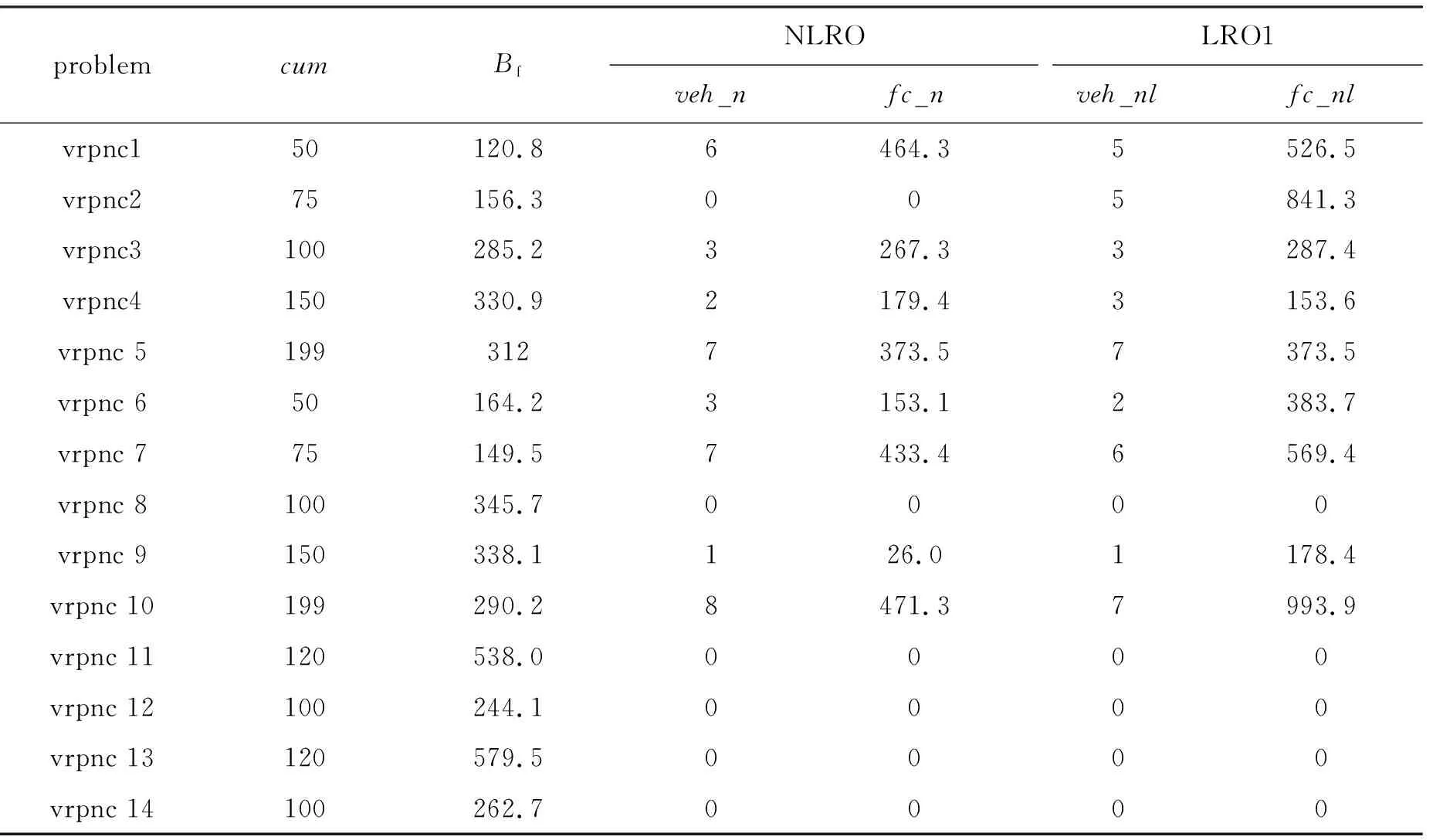
表4 vrpnc問題的優(yōu)化性能分析

針對表3和表4中veh_n和veh_nl兩列數(shù)據(jù)，利用Wilcoxon秩和檢驗進行分析，在違約車輛數(shù)的優(yōu)化能力方面，兩者無顯著差異(p>0.05)。對于表3和表4中fc_n和fc_nl這兩列數(shù)據(jù)，利用Wilcoxon秩和檢驗進行分析，分析結果表明，NLRO產(chǎn)生的懲罰成本顯著小于LRO1(p<0.05)。LRO1單純以違約車輛數(shù)最小為優(yōu)化目標，可能存在多個違約車輛數(shù)相同的算法優(yōu)化解，當?shù)鷹l件終止時，輸出的不一定是總懲罰成本最小的算法優(yōu)化解。與LRO1不同，NLRO兼顧違約車輛數(shù)和總懲罰成本兩個因素。因此，NLRO算法優(yōu)化解對應的總懲罰成本低于LRO1。

表3和表4數(shù)據(jù)表明：對中小規(guī)模和大規(guī)模測試數(shù)據(jù)而言，AGA均具有在有限時間內(nèi)發(fā)現(xiàn)最優(yōu)解的能力。根據(jù)性質(zhì)2，使用AGA求解表2和表3中的算例對應的未發(fā)現(xiàn)最優(yōu)解的概率的范圍在[0.000 1,0.000 7]之間，因此，此時的算法優(yōu)化解表現(xiàn)出了性質(zhì)1所描述的最優(yōu)解相類似的性質(zhì)。

3.3 AGA的求解性能分析

以文獻[15]提到的超啟發(fā)式遺傳算法作為AGA的對比算法，記為S-HPSO。使用兩種算法對NLRO獨立求解30次。S-HPSO與AGA采用相同的初始染色體種群。S-HPSO的相關參數(shù)設置詳見文獻[15]。S-HPSO與AGA遍歷的可行解總數(shù)相同。其他參數(shù)設置詳見第3.1小節(jié)。分別將兩種算法對應的30次運算結果的平均值、標準差、最差適應度函數(shù)值、最好適應度函數(shù)值、運算時間的均值記錄于表5中。表5中標有“*”的測試數(shù)據(jù)表示算法搜索到最優(yōu)目標函數(shù)值為0的最優(yōu)解。

在表5中，Avg_a和Avg_s分別表示兩種算法在30次運算結果中所有最優(yōu)適應度函數(shù)值的平均值，這兩列中的括號內(nèi)數(shù)字表示該測試數(shù)據(jù)搜索到模型最優(yōu)解的次數(shù)。Std_a和Std_s分別表示兩種算法在30次運算結果當中所有最優(yōu)適應度函數(shù)值的標準差。Tavg_a和Tavg_s分別表示兩種算法對應的平均運行時間。

對表5中Avg_a和Avg_s這兩列數(shù)據(jù)進行Wilcoxon秩和檢驗， 結果表明AGA的平均求解性能顯著優(yōu)于S-HPSO的假設成立(p<0.05)。對表5中Tavg_a和Tavg_s這兩列數(shù)據(jù)進行Wilcoxon秩和檢驗，結果表明兩種算法的平均運行時間不存在統(tǒng)計學差異(p>0.05)。雖然AGA增加了利用預期適應度函數(shù)篩選更新規(guī)則環(huán)節(jié)，但這部分運算時間的增加不足以引起統(tǒng)計量秩次的變化，因此，兩者在平均運算時間上不存在統(tǒng)計學差異。

表5 算法統(tǒng)計特性的比較與分析

4 結論

對OVRP-UT建立弱魯棒優(yōu)化模型并求解，核心內(nèi)容如下： ①模型方面，基于現(xiàn)有的弱魯棒優(yōu)化的框架構建了針對OVRP-UT的弱魯棒優(yōu)化模型；②算法方面，設計AGA求解NLRO，提高了啟發(fā)式算法發(fā)現(xiàn)最優(yōu)解的概率，且所得算法優(yōu)化解更接近于最優(yōu)解。

目前求解不確定型車輛路徑問題的魯棒優(yōu)化模型的啟發(fā)式算法主要是元啟發(fā)式算法，下一步研究應關注如何使用超啟發(fā)式算法求解不確定型車輛路徑問題的魯棒優(yōu)化模型。