中小企業貸款風險管理技術創新

吳慶祥

摘要：在分析中小企業融資的現狀及問題的基礎上，從中小企業融資和銀行風險管理兩方面需求出發，創新性設計了一款帶擔保的雙邊信用違約互換產品：利用資產擔保和第三方擔保，重構信用違約互換交易模式。運用KMV模型和現金流模型，計算合約標的公司的違約率以及各個參與主體的收益。通過蒙特卡羅仿真，發現該產品能夠降低企業貸款的風險程度，提高銀行和公司整體的現金流入。該研究結果為解決中小企業融資問題提供了新思路。

關鍵詞：中小企業融資;信用違約互換;雙邊擔保;蒙特卡羅

Abstract： Based on the analysis of the current situation and problems of the small and medium-sized enterprises（SMEs） financing， considering the needs of SME financing and bank risk management， this paper innovatively designs a guaranteed bilateral credit default swap product： which uses asset guarantee and third party guarantee to reconstruct the credit default swap trading model. KMV model and cash flow model are used to calculate the default rate and the income of each participant. Through Monte Carlo simulation， it is found that the product can reduce the risk degree of enterprise loan and increase the cash inflow of banks and companies as a whole. The research results provide new ideas for solving the financing problem of SMEs.

Key words： the small and medium-sized enterprises（SMEs） financing;credit default swap;bilateral guarantees;Monte Carlo

0? 引言

中小企業是我國國民經濟的重要組成部分，在我國經濟和社會發展中愈發重要。近年來，中小微企業總量規模不斷擴大，成為吸納社會就業、穩定增長、改善民生的重要力量。

國家統計局數據顯示，2018年末，中小微企業吸納就業人員23300.4萬人，比2013年末增加增長5.5%。占全部企業就業人員的比重為79.4%。同時，中小企業是市場經濟最活躍的群體，是技術創新的生力軍。我國65%的專利、75% 以上的技術創新、80% 以上的新產品開發，都是由中小企業完成的[1]。然而金融機構對中小企業惜貸，因為中小企業的市場淘汰率遠遠高于國有大中型企業，銀行貸款給中小企業要承擔更大的風險[2]。

由于中小企業自身抗風險能力較弱，更容易受到外部不確定因素的沖擊，生產經營面臨著不同程度的挑戰，加大了融資信貸需求。連日來，相關部門密集出臺金融政策，引導金融機構進一步提高對中小企業信貸投放、減輕中小企業負擔，確保中小企業貸款不受疫情沖擊。然而，銀行也面臨來自監管部門的外部考核要求、銀行內部對于高風險信貸的嚴格的考核指標和追責壓力，以及自身作為現代企業追求經濟利益的根本原則。

因此，如何緩解國內中小企業現階段的融資貸款需求，與銀行信貸風險的防范與防控的矛盾，破解中小企業融資難題和推動技術創新問題，具有重要的理論和現實意義。

1? 產品設計

1.1 產品運行機制

本文選取雙邊信用違約互換作為企業貸款風險防控的基礎模式，此外加上資產擔保和第三方擔保作為信用增級手段。為了清晰的展示產品運行機制，本文繪制企業現金流的流動圖如圖1。

分析圖1可知，期初時，政策性銀行貸款給大型企業，與商業性銀行簽訂一份以大型企業為標的信用違約互換合約，政策性銀行定期支付固定費用給商業性銀行。期末時，如果大型企業沒有發生違約，大型企業支付貸款本息給政策性銀行，商業性銀行不需要支付任何現金給政策性銀行。如果大型企業發生違約，政策性銀行回收部分貸款，剩下貸款損失則由大型企業提供的資產擔保和商業性銀行賠付。

期初時，商業性銀行貸款給中小企業，與政策性銀行簽訂一份以中小企業為標的信用違約互換合約，商業性銀行定期支付固定費用給政策性銀行。此外，中小企業尋求第三方擔保機構提供擔保以進行信用增級。中小企業定期支付擔保費給擔保機構。期末時，如果中小企業沒有發生違約，中小企業支付貸款本息給政策性銀行，政策性銀行不需要支付任何現金給商業性銀行。如果中小企業發生違約，商業性銀行回收部分貸款，剩下貸款損失則由政策性銀行和擔保機構賠付。

1.2 產品基本要素和定價

1.2.1 基本假設

為了簡化模型和減少運算量，本文提出以下假設：

①政策性銀行和商業性銀行在期末時只受貸款本金，不收利息。因此只考慮貸款本身，銀行在期末時只有盈虧平衡和虧損兩種情況。

②定義大型企業違約的情況：大型企業的某項業務收入在期末時低于貸款本金，此時大型企業該項業務無法償還全部貸款本金，只能以公司資產擔保以償還剩下貸款本金。定義中小企業違約的情況：中小企業的公司價值在期末時低于貸款本金，中小企業因為規模較小無法進行擔保，只能由第三方擔保機構償還剩下貸款本金。大型企業和中小企業貸款發生違約時，風險分擔順序如圖2。

③大型企業和中小企業只有貸款到期時才會違約。

④大型企業和中小企業貸款均為一次性到期付本金。

⑤除了合約費用，忽略其他交易成本。

1.2.2 以大型企業為標的信用違約互換合約

本文參考劉曉桐[3]的研究，采用KMV模型，計算合約標的公司的違約率，結合歷史數據所得的回收率和貸款本金，最終推出信用違約互換合約的價格。合約定價推導過程中涉及的參數如表1。

為了呈現大型企業某項未來業務收入的不確定性，假設業務收入服從布朗運動，即：

因此企業的業務利潤可以看成一個以歐式看漲期權，行權時間為貸款到期日，標定為業務收入，執行價為貸款成本。若企業的業務收入高于貸款成本，則企業執行合約，返還全部貸款給銀行，剩下留為企業利潤。若企業業務收入低于貸款成本，則企業不執行合約。此時企業屬于違約情況，企業將業務收入全部給銀行，剩下未償還的貸款由資產擔保和商業性銀行提供。業務收入、利潤和貸款成本關系如下：

聯立上述方程組，通過matlab的fsolve函數進行迭代求解VA和？滓A，由于上述方程為非線性方程，采用Levenberg-Marquardt算法進行運算。

KMV模型假設一旦公司資產（對大型企業而言，即業務收入）低于某一闕值（違約點），即可判斷公司違約。以往的研究一般取公司短期負債水平和長期負債水平的加權平均和為違約點;本文根據所設計的合約特點，直接取違約點為貸款成本，DPT=D。違約距離計算公式如下：

1.2.3 以中小企業為標的信用違約互換合約

該份信用違約互換合約價格求解方法和上述求解方法基本相同，只是需要求解前，將企業某項業務收入換成企業資產價值，將業務利潤換成股權價值，將業務成本換成負債成本（貸款成本）。

1.2.4 以大型企業為標的資產擔保

參考目前已有的研究可知，往往銀行貸款給大企業時會硬性要求提供企業其他資產的資產擔保，也不會支付給企業資產擔保費。

本文假設大型企業的資產擔保是在商業性銀行賠付到一定程度后產生的，即商業性銀行存在賠付最大值。假設商業性銀行賠付最大值占貸款總額的一定比例？姿1，因此以大型企業為標的信用違約互換中的貸款成本同樣占貸款總額的一定比例？姿1。

1.2.5 以中小企業為標的第三方擔保

本文假設擔保機構的擔保是在政策性銀行賠付到一定程度后產生的，即政策性銀行存在賠付最大值。假設政策性銀行賠付最大值占貸款總額的一定比例？姿2，因此以中小企業企業為標的信用違約互換中的貸款成本同樣占貸款總額的一定比例？姿2。

以中小企業為標的第三方擔保可以看成以中小企業資產為標定，信用違約互換中的貸款成本為執行價，行權時間為貸款到期日的歐式看跌期權。當公司資產低于貸款成本時，中小企業執行合約，擔保機構賠付超出信用違約互換貸款成本的貸款損失部分。因此可以采用歐式看跌期權公式計算擔保費，即中小企業尋求擔保機構提供擔保主要支出的費用。由于篇幅限制，本文不羅列歐式看跌期權公式。

1.3 銀行現金流和擔保機構現金流分析

為了分析設計的產品降低企業貸款風險的效果，本文分別在帶擔保雙邊信用違約互換、只有擔保的情況下，分析政策性銀行和商業性銀行、擔保機構在貸款到期時的現金流。

1.3.1 帶擔保雙邊信用違約互換的情況

政策性銀行期末現金流1=-貸款總額支出（大型企業）+貸款回收值+商業性銀行賠付+資產擔保賠付-信用違約互換1支出+信用違約互換2收入-賠付中小企業損失。商業性銀行期末現金流1=-貸款總額支出（中小企業）+貸款回收值+政策性銀行賠付+擔保機構賠付-信用違約互換2支出+信用違約互換1收入-賠付大型企業損失。擔保機構1=+擔保費收入-超出信用違約互換貸款成本的貸款損失賠付。

上述方程中，貸款回收，即企業違約時企業將業務收入值或者企業資產值全部用來償還給銀行。此外，商業性銀行賠付大型企業損失最大值不超過貸款總額×？姿1;政策性銀行賠付中小企業的損失最大不超過貸款總額×？姿2。超出的部分由擔保公司或者資產擔保提供。

1.3.2 只有擔保的情況

政策性銀行期末現金流2=-貸款總額（大型企業）+貸款回收值+資產擔保賠付。商業性銀行期末現金流2=-貸款總額（中小企業）+貸款回收值+擔保機構賠付。

2? 產品實證分析

為了檢驗該合同在實操性和有效性，首先設定篩選標準，選取一家大型企業的某項業務和一家中小企業。通過WIND數據庫獲取國內21個市場行業指數，時間跨度為2018年6月19日至2019年6月19日一年的長度，通過STATA軟件進行處理，統計出行業之間的相關系數矩陣。選取相關性最弱的兩個行業：互聯網與收獲目錄零售行業、能源設備與服務業行業，相關系數為0.3785。接著，根據信用違約互換定價原理，合約中貸款企業貸款規模應該相近，由于本文作為參考的企業是大型企業與中小企業，風險與企業規模不同，所以本文以中小企業總資產規模與大型企業營業收入相匹配為標準，分別在科創板選取深圳傳音控股股份有限公司作為中小企業，選取廣匯能源股份有限公司為大型企業。

為了減少兩份互換合約的貸款本金不相等造成的風險敞口，本文設定：

查詢歷史數據可知，廣匯能源業務成本為48億元。假設廣匯能源該項業務資金來源全部為銀行貸款，因此對應的CDS1貸款本金為33.6億元。傳音控股公司債務為55億元，假設公司債務全部為銀行貸款，根據上述等式，可以反推2=0.61，對應的CDS2貸款本金為33.6億元。

接下來通過蒙特卡羅仿真，模擬銀行未來現金流情況，最終求出銀行未來現金流的預測值。本文數據來源為wind數據庫，所選數據的時間跨度為2009年-2018年的年度財務報告數據。蒙特卡羅仿真次數為10000次，步數為100次。

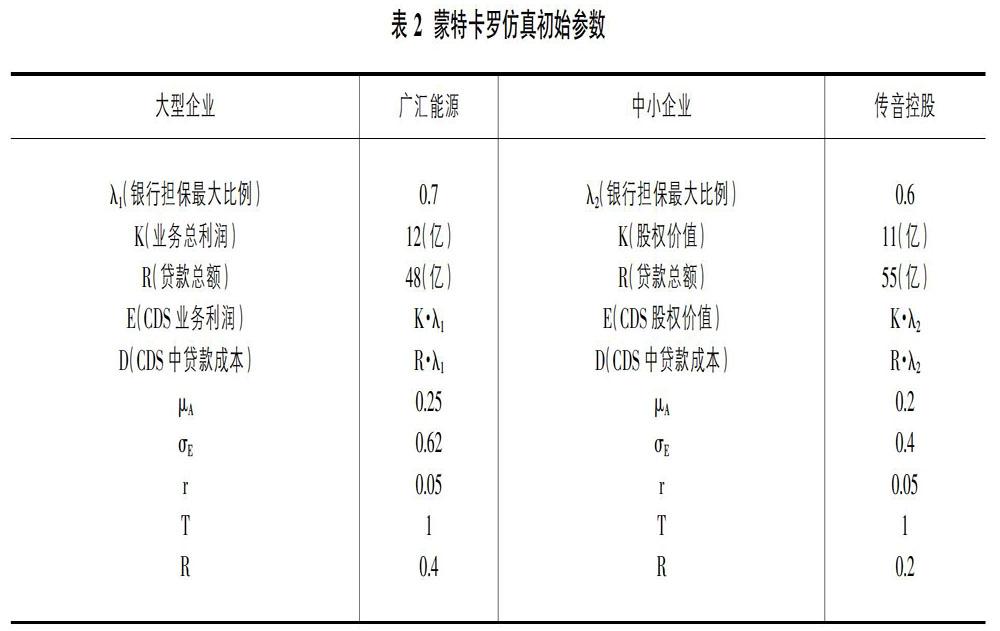
初始參數值如表2。

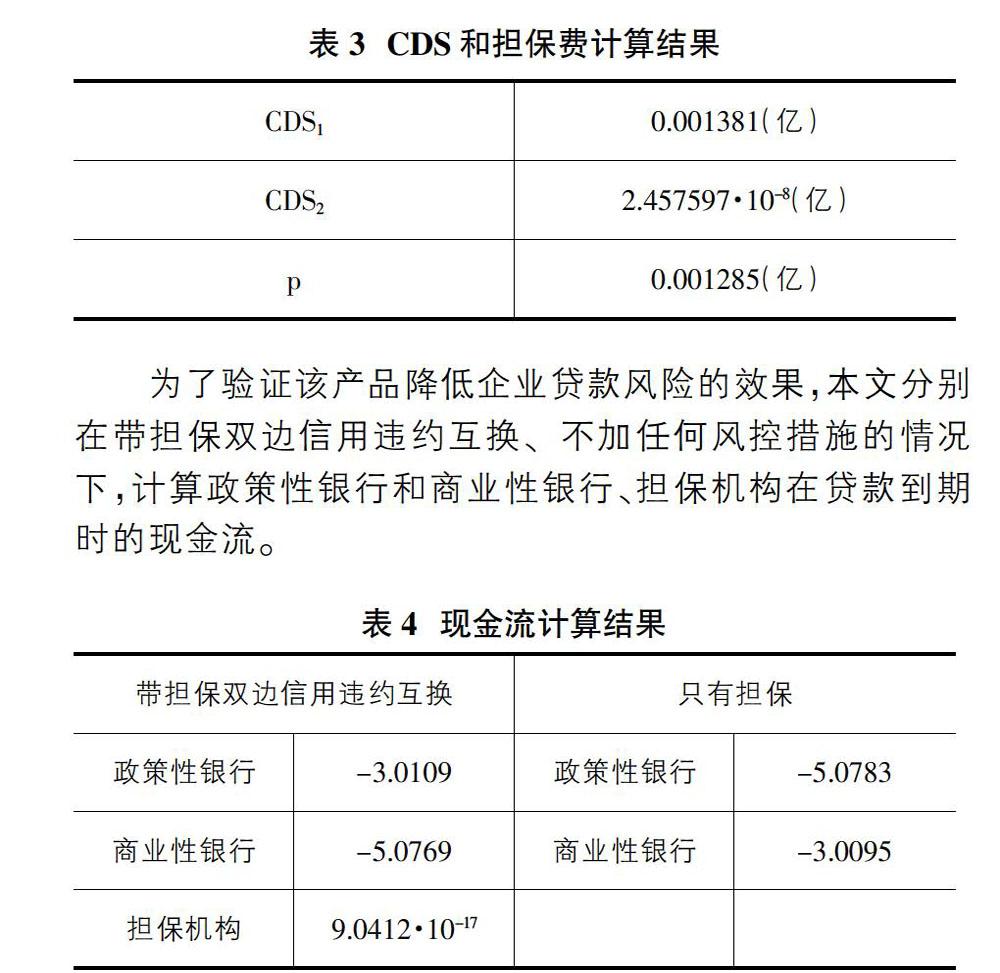
通過蒙特卡羅仿真，計算可得以大型企業為標的信用違約互換合約CDS1、以中小企業為標的信用違約互換合約CDS2還有第三方擔保費用p如表3。

為了驗證該產品降低企業貸款風險的效果，本文分別在帶擔保雙邊信用違約互換、不加任何風控措施的情況下，計算政策性銀行和商業性銀行、擔保機構在貸款到期時的現金流。

2.1 結果分析

定義？駐為產品降低企業貸款風險的程度，即為帶擔保雙邊信用違約互換的政策性銀行和商業性銀行現金流之和，減去只有擔保的政策性銀行和商業性銀行現金流之和。計算可得？駐=5.8531·10-13>0。

分析可知，由于選取的大型企業波動率較大，風險溢價較高，因此對應的信用違約互換合約價格較高，同理中小企業對應的信用違約互換合約價格較低。在實際市場中，該產品可以實現凈現金流交割，即政策性銀行支付給商業性銀行0.001381-2.457597·10-8=0.0013806（億）。？駐>0說明帶擔保雙邊信用違約互換的兩家銀行現金流有所提高。此外，擔保機構的期望現金流也是正數，擔保機構通過收取擔保費盈利，由于擔保機構擔保順序靠后，擔保金額較低，中小企業發生違約的金額達到擔保機構需要賠付的情況較少，因此期望現金流為正數。綜上，該產品有效降低了銀行的貸款風險，并且實現了銀行和擔保機構共贏。

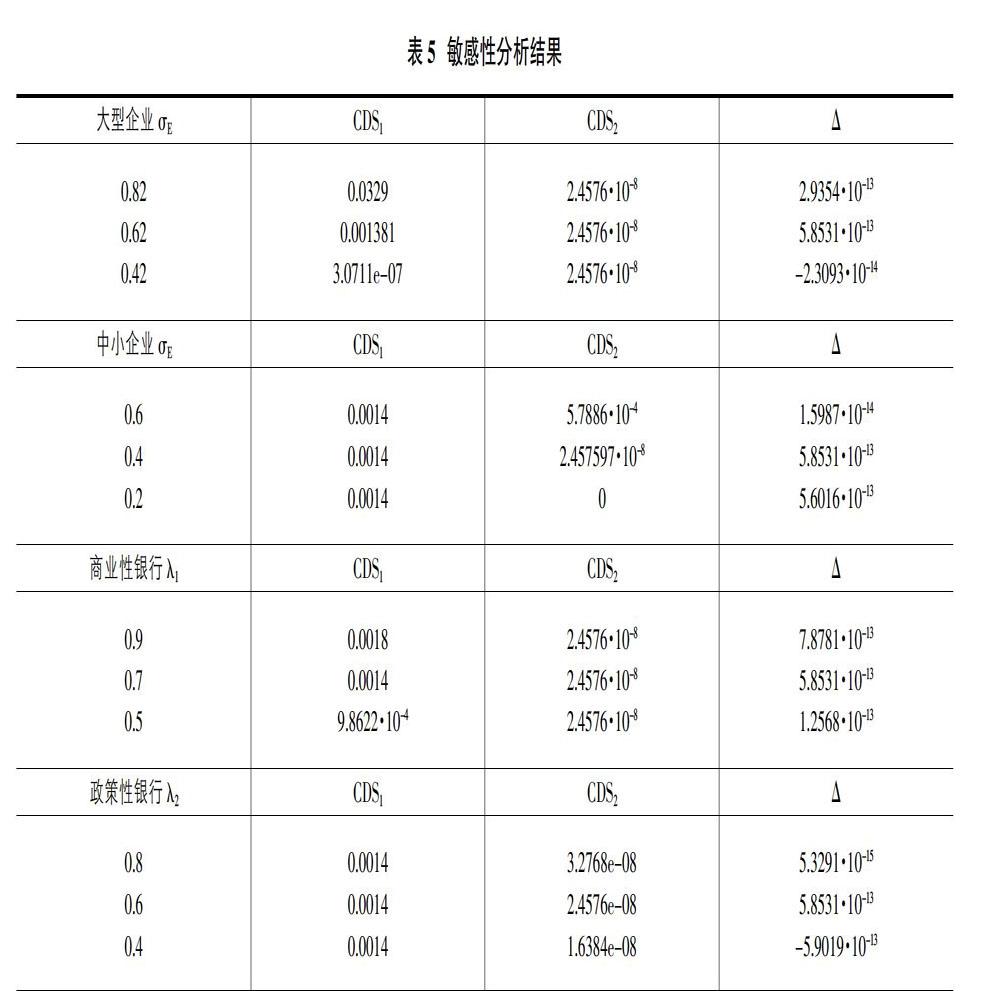
2.2 敏感性分析

在合約條款里，企業業務利潤的波動率（或者企業股權的波動率）、政策性銀行或者商業性銀行擔保最大值對應的比例為關鍵參數。為了檢測該產品的生存能力，對產品的參數進行敏感性分析如表5。

由表5可知，信用違約互換合約與業務利潤的波動率（或者股權的波動率）、政策性銀行或者商業性銀行擔保最大值對應的比例均成正比。分析可知，波動率越大，銀行擔保最多，銀行承擔的貸款風險也就越高，因此對應的信用違約互換合約價格也就越高。此外，隨著波動率的增大，產品降低企業貸款風險的程度呈“拋物線”先增加后減少。因此選取的貸款企業的波動率過高或者過低，產品降低企業貸款風險的程度都會減弱。對商業性銀行來說，擔保比例越大，產品降低企業貸款風險的程度就越高。對政策性銀行來說，擔保比例越大，產品降低企業貸款風險的程度呈“拋物線”先增加后減少，因此可能存在最優擔保比例。

參考文獻：

[1]財政部財政科學研究所課題組，蘇明.我國中小企業發展支持政策研究[J].經濟研究參考，2015（08）：3-22.

[2]郭星溪.中小企業融資圃境與對策探討[J].經濟與管理研究，2009（08）：73-90.

[3]劉曉桐.基于KMV模型的國內信用違約互換定價及實證研究[D].南京大學，2017.