高分七號衛星太陽翼驅動主動控制方案

郭超勇 陸棟寧 陳超 張猛 于國慶

(北京控制工程研究所，北京 100094)

高分七號衛星是我國“高分”系列中測繪精度要求最高的衛星，可以實現民用1∶10 000比例尺衛星的立體測繪。衛星搭載了高分辨率雙線陣立體相機、激光測高儀等有效載荷，可以實現地面物體的亞米級立體成像。高精度、高分辨率的有效載荷對高分七號衛星控制平臺的姿態穩定度提出了更高的要求。與以往低軌遙感衛星平臺0.000 5(°)/s(3δ)的衛星姿態穩定度相比，高分七號衛星的姿態穩定度指標要求提高到0.000 1(°)/s(3δ)，衛星平臺擾動量約為原有低軌遙感衛星平臺的1/5。

太陽翼驅動機構(SADA)是影響衛星姿態控制性能的主要擾動源之一[1-2]。傳統SADA一般都采用步進電機作為驅動源，具有定位精度高、無累積誤差和易于開環控制等優點[3-4]。我國低軌遙感衛星平臺SADA大都采用這種形式。SADA步進電機的諧波力矩、相對運動部件的摩擦力矩及太陽翼撓性等多種因素的綜合作用，使得太陽翼在保持對日定向的連續轉動過程中出現速率波動，并對太陽翼的撓性模態產生激勵，因此衛星平臺姿態穩定度很難得到更高的提升。目前，國內外也有通過衛星姿態動力學控制去補償太陽翼撓性部件產生的擾動的方法[5-7]，但仍難以滿足高分七號衛星平臺的極高姿態穩定度要求。

與傳統SADA采用步進電機作為驅動源的方案完全不同，本文提出一種應用永磁同步電機(PMSM)的高穩定度太陽翼驅動主動控制方案，通過旋轉變壓器采集太陽翼的轉動角度并實現反饋控制。采用針對PMSM驅動大慣量撓性負載的相位補償控制策略，實現高分七號衛星驅動太陽翼的高穩定性控制和引起的衛星姿態擾動的主動抑制。太陽翼驅動主動控制方案在高分七號衛星得到了成功應用，最后的試驗結果也證明了方案的有效性。

1 應用PMSM的太陽翼驅動主動控制方案

1.1 方案概述

高分七號衛星高穩定度SADA用于驅動衛星2副太陽翼。太陽翼展開以后，高穩定度SADA接收控制分系統控制器的控制指令，驅動2副太陽翼按照指定角速度旋轉，保證太陽翼總能夠面對太陽光的入射方向。與傳統步進電機驅動型SADA不同，高穩定度SADA采用PMSM直接驅動，實現太陽翼的高穩定度閉環控制。PMSM驅動系統中采用旋轉變壓器實現角度測量和轉速計算，同時通過高精度電流采樣電路實現電機電流的高速、高精度采樣，進而實現轉速、電流等多環閉環控制。

1.2 PMSM模型

PMSM矢量控制系統通常采用轉子同步旋轉直軸-交軸(d-q)坐標系下的數學模型。在幅值不變原則下，考慮表貼式PMSM轉子永磁磁鏈Ψr不變，以d軸和q軸電流為狀態變量的電機方程如下[8]。

(1)

式中：id和iq為定子側的d軸和q軸電流；ud和uq分別為定子側的d軸和q軸電壓；Rs為定子側電樞電阻；Ls為定子側的等效電感；ωr為轉子機械角頻率；pn為轉子極對數。

考慮太陽翼沿驅動軸的轉動慣量為Js，電機轉子轉動慣量為Jm，且Jm?Js，負載轉矩為TL，電磁轉矩為Te，那么電機轉子機械運動方程為

(2)

電磁轉矩方程為

(3)

式(1)～(3)構成了PMSM在d-q坐標系下的狀態方程。從狀態方程可以看出，不考慮其他復雜的非線性因素，PMSM驅動剛性負載的動力學系統已經是一個多變量三階耦合系統。

1.3 太陽翼動力學模型

SADA驅動太陽翼對日定向，是太陽翼與衛星本體連接的機電部件。高分七號衛星太陽翼與SADA連接示意如圖1所示。

目前城市建筑所主要采用的中水回用系統，根據中水回用的管道架設方式，主要分為直接回用和間接回用兩種類型。

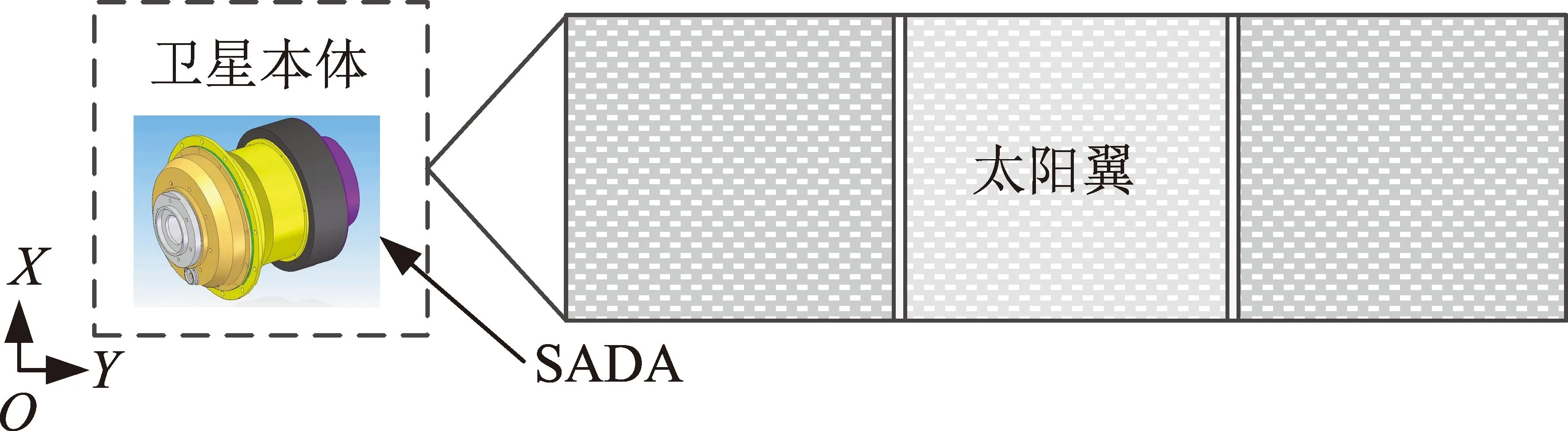
圖1 太陽翼安裝示意Fig.1 Solar array connection diagram

考慮太陽翼撓性，其運動可分解為轉動運動與撓性振動的耦合。文獻[9]中提出了撓性太陽翼高階模態的動力學模型，然而，當模態階數較大時，其廣義慣量矩陣接近奇異。為了便于工程設計和分析，可僅考慮一階撓性模態的太陽翼驅動動力學方程。

(4)

式中：δ為耦合系數，考慮負載撓性時有δ2=Jf，其中Jf為撓性負載的等效慣量；η為撓性模態變量；φ為撓性模態速率；模態阻尼D=2ξωf，其中，ξ為阻尼比，ωf為一階撓性模態角頻率；模態剛度K=ωf2。

1.4 特性分析

PMSM高性能控制一般采用基于轉子磁場的矢量控制，在伺服驅動場合實現速度外環及電流內環控制。采用id=0的矢量控制策略，聯立電機驅動方程(1)與太陽翼一階模態狀態方程(4)，則得到系統的動力學模型如下。

(5)

由于速度環與電流環帶寬差別較大，可以認為在速度外環進行調節時，電流內環已經調節完成。因此，在速度環設計時，可不考慮電流環的影響。PMSM驅動系統速度環一般采用傳統比例積分(PI)調節器，結合式(5)描述的PMSM驅動太陽翼負載構成的控制框圖如圖2所示。

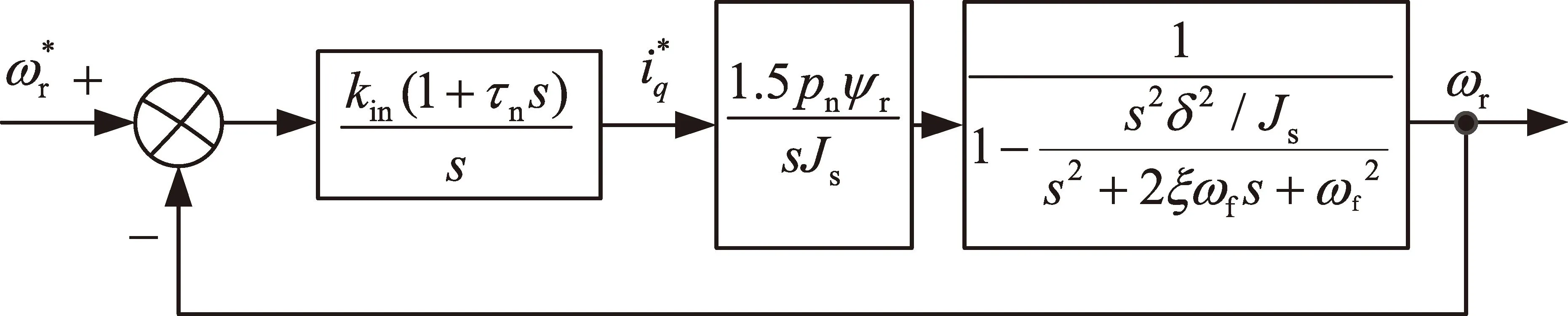
注：為太陽翼指令轉速；kin為積分系數；τn為積分時間常數；s為頻率域。

此時速度外環傳遞函數可以描述為

(6)

速度環截止頻率ωc與PI調節器參數之間的關系如下。

(7)

相位裕量pm為

pm=arctan (ωcτn)

(8)

為了滿足系統足夠的擾動抑制能力，需要達到一定的控制帶寬，比例、積分系數與系統的轉動慣量成正比。通過調整速度環積分常數和比例常數，可以提高系統剛度和阻尼，使太陽翼轉速更快地收斂到期望值附近，實現太陽翼的高剛度、高穩定度驅動控制。由于系統的驅動能力和角度測量分辨力限制，PI調節器參數并不能成比例增加。采用傳統PI控制方法進行相位裕量分析，其Bode圖如圖3所示。

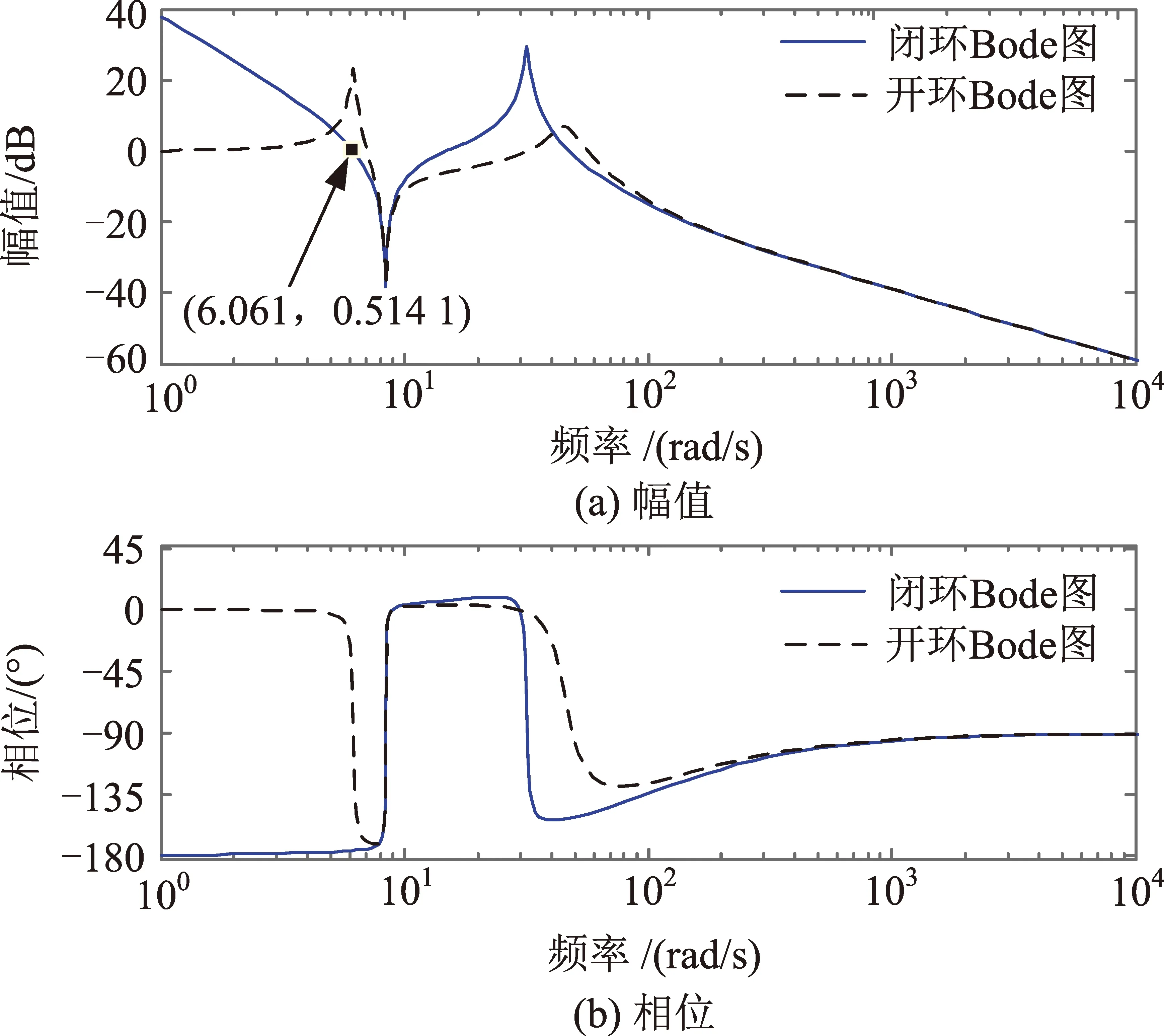
圖3 采用傳統PI調節器的撓性負載Bode圖Fig.3 Flexible load Bode diagram using traditional PI regulator

2 相位補償控制策略

SADA與撓性太陽翼之間不設減速裝置，因此太陽翼的任何特性和擾動都將毫無保留地傳遞至驅動電機的輸出軸，這無疑增加了驅動機構的控制難度[10]。同時，太陽翼的慣量一般都非常大，且具有弱阻尼、大撓性等特點[11]，采用傳統PI調節算法并進行參數整定方法對實現高性能太陽翼控制非常困難，容易使系統控制變得不穩定。其根本原因在于PI調節器只能提供一個處于原點的極點和一個可配置的零點，對較高階次系統的整定能力有限。為了提高系統的相位裕量，設計相位補償器進行補償。為充分發揮超相位補償器的能力，設計時應重點考慮增加相位裕度，同時盡可能使最大超前相角的頻率點與相位補償后的開環系統剪切頻率相重合。采用相位補償校正網絡，其傳遞函數設計如下。

(9)

式中：分度系數α>1；T1為時間常數。

超前相位補償網絡的主要作用是使系統的相位裕度角超前，只要將超前補償網絡的交接頻率1/αT1和1/T1選取在待補償系統截止頻率兩旁，并適當選擇參數α和T1，就可以使系統的截止頻率和相角裕度滿足系統穩定性的要求。

為進一步分析其性能，根據相位補償網絡傳遞函數，可得到其最大超前相角為

(10)

分析可知，最大超前相角與分度系數α有關，較大的α可以提供更大的超前相角。隨著α的增大，系統對高頻噪聲將變得非常敏感，容易引入高頻干擾。因此，在相位補償網絡的設計中應適當選取α，使系統具有足夠相位裕量，且高頻噪聲干擾不明顯。為了抑制相位補償網絡的高頻干擾，設計低通濾波器，實現對高頻干擾的進一步抑制。引入相位補償控制策略后的控制結構見圖4。

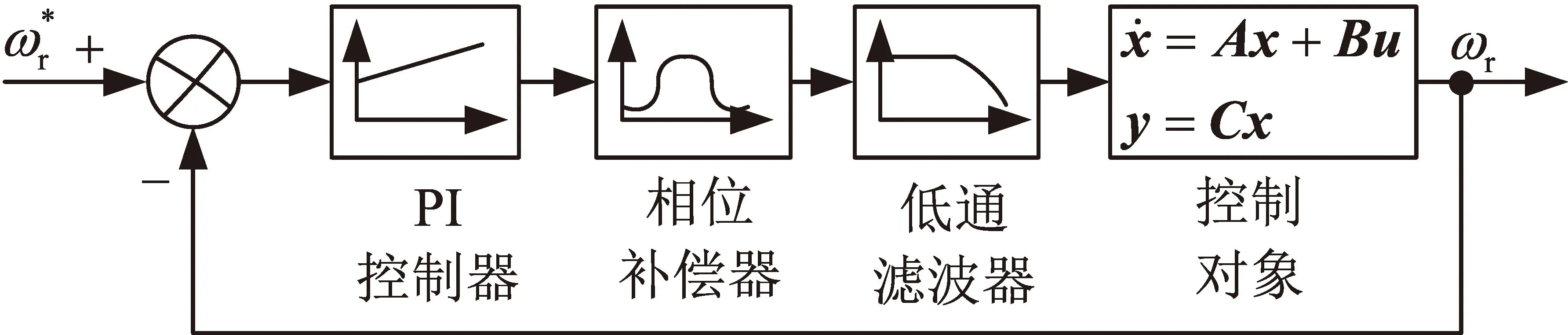
注：x為狀態變量；y為輸出變量；u為輸入信號；A為控制對象系數矩陣；B為控制對象輸入矩陣；C為控制對象輸出矩陣。

高分七號衛星撓性太陽翼負載驅動系統采用相位補償控制策略的Bode圖，如圖5所示。

通過對比圖5與圖3可知：采用相位補償策略后，相位裕量增加至41°，相對相位補償前得到極大的提升；而且增加分度系數α，還能進一步增加相位裕量，但同時也意味著控制帶寬更加靠近一階模態頻率，易引起系統的諧振。在實際設計時，相位補償后驅動系統的截止頻率并沒有在相位補償網絡的中心頻率處，避免與太陽翼的撓性模態耦合產生諧振。

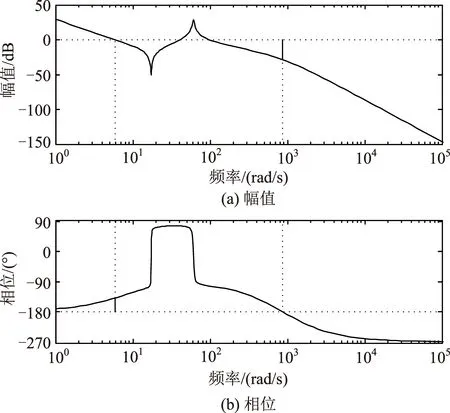
圖5 采用相位補償網絡驅動撓性負載Bode圖Fig.5 Bode diagram using phase compensation network driving flexible load

3 試驗結果及分析

為了驗證本文提出的相位補償策略的有效性，進行PMSM直驅型SADA驅動高分七號衛星太陽翼模擬負載的試驗驗證。驅動裝置及太陽翼參數見表1和表2，電流環控制周期時間常數為250 μs，速度環控制周期時間常數為1 ms。

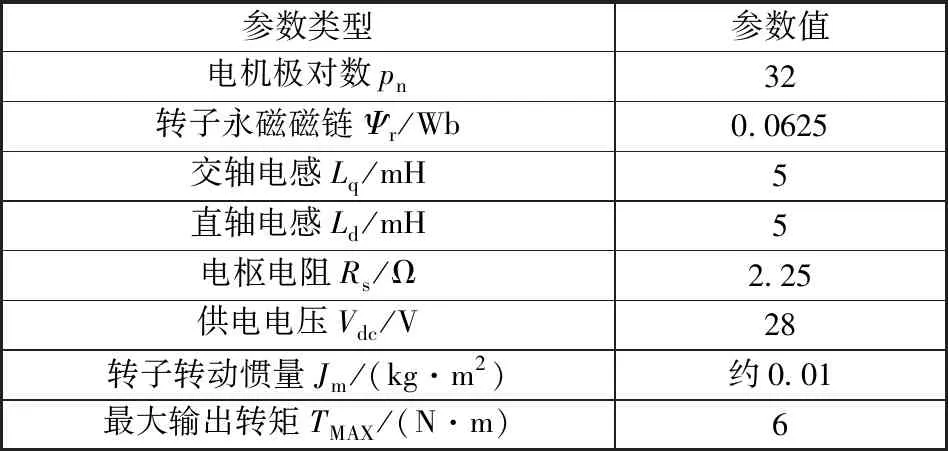
表1 驅動機構電機參數Table 1 Motor parameters of drive mechanism

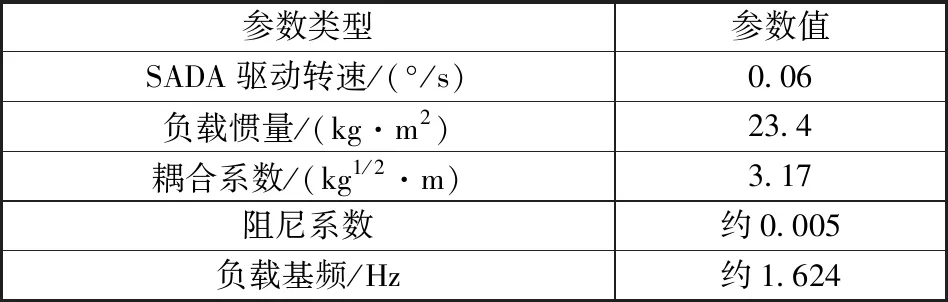
表2 太陽翼模擬負載參數Table 2 Solar array simulation load parameters

圖6描述了高分七號衛星SADA驅動太陽翼模擬負載狀態下從零速切換至巡航轉速(0.06 (°)/s)的角速度波動情況。由于測角裝置的分辨力限制，在極低角速度給定狀態下，速度測量結果采用機構角位置進行周期為100 ms差分，并將計算得到的角速度值繪成曲線。角速度曲線上存在低頻脈動，這些脈動主要是由于撓性太陽翼模態頻率與控制帶寬綜合作用產生的低頻擾動。SADA驅動太陽翼在啟動時轉速響應輸出存在超調，在大約4個調整周波之后SADA運行到穩態工況，轉速波動較小，轉速波動值為3.5%(100 ms周期，1δ)。

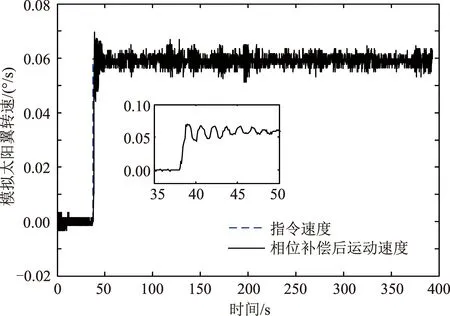
圖6 驅動太陽翼模擬負載角速度曲線Fig.6 Angular velocity curve when driving solar array simulation load

為了驗證高穩定度SADA及主動控制方案的優勢，建立傳統步進電機型SADA與采用PMSM的太陽翼主動控制方案對衛星擾動力矩的測量平臺，并對衛星的擾動力矩進行對比分析，結果如圖7所示。

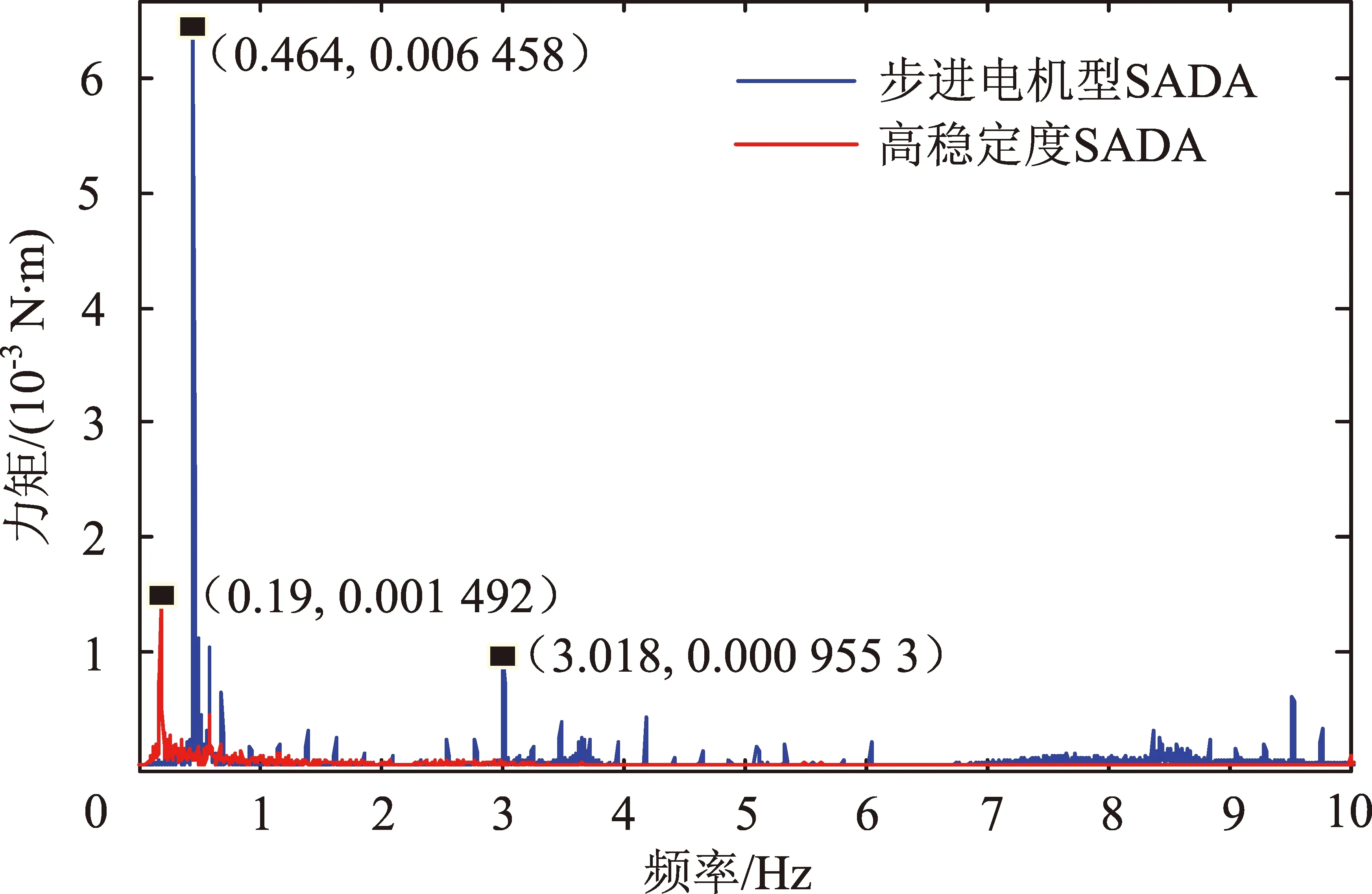
圖7 衛星姿態擾動對比結果Fig.7 Comparison results of satellite altitude disturbance

由對比情況可知，基于本文方案的擾動力矩相比傳統步進電機的擾動力矩減少超過50%。從頻率成分來分析，在低頻段，除了固有頻率(0.2 Hz)外，本文方案幾乎沒有任何擾動頻率；在高頻段，也不存在由于電流細分引起的步進頻率(0.232 Hz)倍頻成分[12]。因此，相比基于電流細分的傳統步進電機型SADA，PMSM直驅型高穩定度SADA具有更好的驅動性能，對衛星姿態穩定度的影響更小。

本文提出的太陽翼驅動主動控制方案成功應用于高分七號衛星。為了對步進電機驅動方案與PMSM驅動方案的驅動穩定性進行在軌性能對比，設計了高穩定度SADA的步進驅動模式和主動控制策略模式，高穩定度SADA在軌進行了模式切換。兩種不同工作模式的在軌試驗結果如圖8所示，采用傳統的步進電機驅動方案，太陽翼的轉速波動量大于100%。采用主動控制策略模式后，太陽翼轉速穩定度得到了極大的提升，通過在軌數據分析得到太陽翼轉速穩定度指標實現優于指標要求。與傳統步進驅動方案相比，在軌轉速穩定度提高了一個數據級以上。進一步通過高分七號衛星Y側的姿態穩定度來看，采用主動控制策略后，衛星的姿態穩定度也優于0.000 1(°)/s(3δ)，太陽翼驅動主動控制方案實現了在軌驗證。

4 結束語

針對傳統SADA采用步進電機對衛星產生較大的姿態擾動問題，本文提出了應用PMSM的太陽翼主動驅動方案，并成功應用于高分七號衛星。針對撓性太陽翼驅動系統采用傳統PI控制策略時存在相位裕量不足的問題，提出了一種相位補償主動控制策略，實現了高穩定度SADA驅動太陽翼的穩定性控制和姿態擾動的主動控制。地面試驗及在軌試驗結果表明：本文提出的太陽翼驅動主動控制方案，不但能實現較高的相位裕量及優良的穩定性，而且顯著地改善了動態性能，同時降低了對高分七號衛星產生的姿態擾動，可為后續其他高分辨率衛星應用提供參考。