萊洛三角形

我們學(xué)習(xí)的三角形三邊都是直線(xiàn)段，那如果三邊變成弧線(xiàn)會(huì)怎么樣呢？

先畫(huà)一個(gè)正三角形，再分別以其三個(gè)頂點(diǎn)為圓心、三角形邊長(zhǎng)為半徑畫(huà)圓，猜猜看，三個(gè)圓的公共部分是什么圖形？

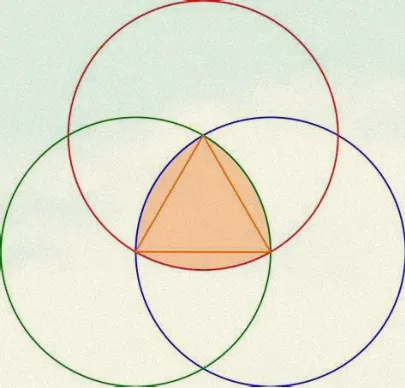
對(duì)啦，這就是萊洛三角形（Reuleaux triangle），是不是像個(gè)減肥成功的圓形啊？它還有個(gè)更通俗的名字：弧三角形。

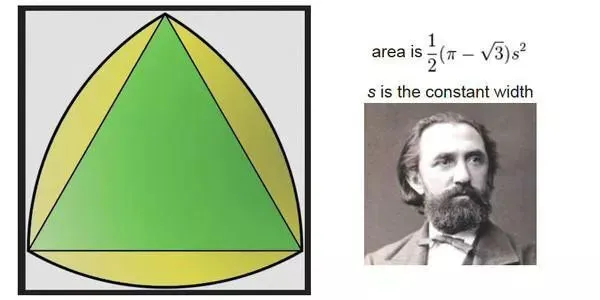
萊洛三角形的應(yīng)用中最著名的就是設(shè)計(jì)汪克爾發(fā)動(dòng)機(jī)的轉(zhuǎn)子了，它還被用來(lái)制成特殊的鉆頭，能鉆出四角為圓弧的正方形的孔。

萊洛三角形到底有什么過(guò)人之處呢？

原來(lái)它是一種等寬曲線(xiàn)（Curve of constant width，或稱(chēng)恒寬曲線(xiàn)）。

小課堂：什么是等寬曲線(xiàn)？

將一個(gè)閉合曲線(xiàn)放在兩條平行線(xiàn)中間，使之與這兩平行線(xiàn)相切，則可以做到：無(wú)論這個(gè)閉合曲線(xiàn)如何運(yùn)動(dòng)，只要它仍與原平行線(xiàn)中的一條直線(xiàn)相切，就必與另一條直線(xiàn)相切，那么此閉合曲線(xiàn)為等寬曲線(xiàn)。

探索時(shí)間：

除了圓形以外，還有什么形狀的窨井蓋不會(huì)掉入下水道？為什么呢？

等寬曲線(xiàn)拓展到三維會(huì)怎么樣呢？