管道系統動力吸振器布置多目標優化設計

王碧浩，熊夫睿，黃茜，張文正

管道系統動力吸振器布置多目標優化設計

王碧浩，熊夫睿，黃茜，張文正

（中國核動力研究設計院 核反應堆系統設計技術重點實驗室，四川 成都 610213）

工業設備中管道系統的振動具有明顯地線譜特征，動力吸振器可以有效抑制管道在特定頻率下的振動。引入一類含平動和轉動自由度的動力吸振器，針對某管道系統開展簡諧激勵下的振動控制研究。首先，分別采用梁單元、彈簧－質量單元模擬管道和動力吸振器，并將動力吸振器與管道的運動方程耦合。采用拉丁超立方體抽樣方法對動力吸振器的參數進行采樣，建立動力吸振器參數到管道支承位置振動響應的輸入輸出關系。采用Kriging插值法建立輸入輸出關系的代理模型，基于代理模型進行參數相關性分析。應用全局高效響應面算法，對管道上動力吸振器的布置進行多目標優化，實現管道系統的振動控制，優化變量包括吸動力吸振器的安裝位置和剛度參數。并針對得到的最優設計方案進行穩健性評估，考查各設計參數在設計方案名義值附近擾動時，對各輸出變量的影響。

多目標優化；動力吸振器；代理模型；減振降噪；相關性分析

管道系統廣泛應用于各類機械設備中，也是振動傳遞的主要途徑之一。在內部流體激勵和外部機械設備激勵的共同作用下，管道極易發生劇烈振動導致性能和可靠性降低，因此對管道系統進行減振優化非常必要[1]。

動力吸振器是一類廉價且易于維護的振動控制元器件，可以有效降低管道在特定頻率下的振動，在低頻振動控制中有著廣泛的應用。動力吸振器通常作為輔助的彈簧質量單元附加在管道系統上，通過調諧質量和剛度參數使之在激勵作用下發生共振，從而將外部激勵的能量轉化為其機械能，進而起到抑制管道系統振動的目的[2]。

然而當復雜管道系統受到多個激勵源作用時，需要采用多個單自由度（分別含平動剛度或轉動剛度）的動力吸振器對其進行減隔振控制。通常需要同時對多個動力吸振器參數及其部署位置進行仔細調諧。本文引入一類含平動和轉動自由度的動力吸振器，針對某管道系統開展簡諧激勵下的振動控制多目標優化研究。

1 控制方程

管道在外部激勵作用下，橫向振動是其主要的變形，根據歐拉－伯努利梁理論，均質梁結構的振動方程為：

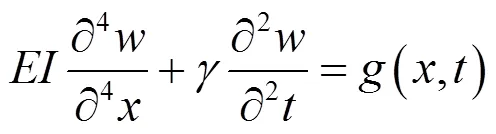
式中：為彈性模量，Pa；為梁的截面慣性矩，m4；為沿梁軸向的質量分布，kg/m；為梁的振動位移，m；(,)為梁所受外載荷，N；為梁的位置坐標，m；為時間，s。

動力吸振器對梁振動的抑制效果通過在主系統上施加的集中力體現，考慮動力吸振器慣性效應作用的梁受迫振動方程為：

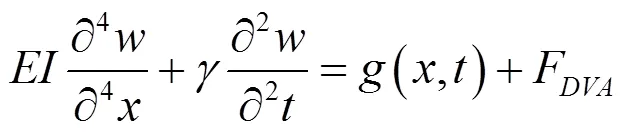
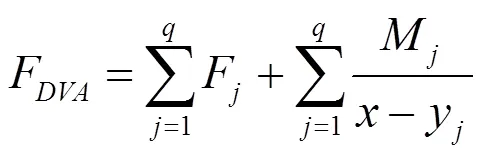
動力吸振器的運動方程為：

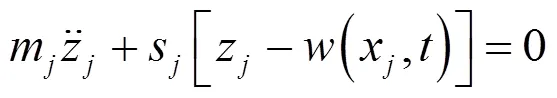
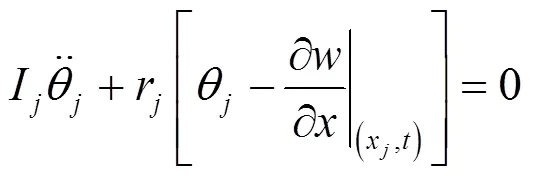
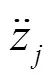
耦合了動力吸振器梁的穩態解為：

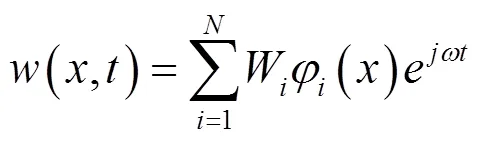
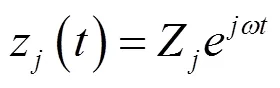
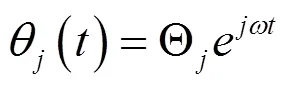
式中：W為模態坐標向量；φ為模態函數；Z為梁在吸振器安裝位置的平動位移，m；Θ為梁在吸振器安裝位置的轉角，rad。

則動力吸振器作用在梁上的力和彎矩分別為：

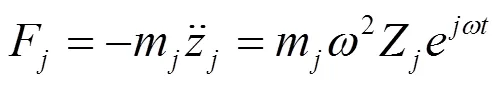
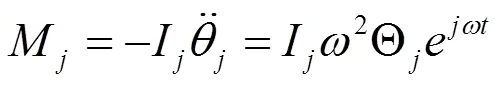
通過模態展開，利用模態函數的正交性和歸一化，可以得出耦合系統的模態坐標，將其代入式（6）～式（8），即可得到系統在穩態下的位移響應[3]。

2 振動分析模型

2.1 結構分析模型

某管道系統根據需要和用途沿管內流體流動方向設置了電動閘閥、電磁閥等閥門。管道系統通過17個支吊架約束，支吊架一端連接在管道上，另一端固定在基座上。為實現管道在系統出入口位置的激勵下各支吊架位置的振動水平下降，本文擬沿管道設置若干動力吸振器，通過優化動力吸振器的參數實現低頻段內的振動被動控制。

為使模型盡量簡化，且又能準確模擬管道系統的振動特性，根據實際結構特征和邊界條件并結合有限元理論，建立管道系統的有限元分析模型。

采用管單元模擬管道，閥門及一些對系統整體剛度影響很小的部件在模型中只考慮其質量影響。支吊架采用彈簧單元模擬，不同支吊架在管道一側的固定方式根據其功能不同約束相應的自由度，支吊架在基座一側約束所有方向的自由度。沿管道布置的動力吸振器采用彈簧－質量單元模擬，并將動力吸振器與管道單元的運動方程耦合。

考慮管道系受到來自進出口位置的單位帶寬激勵，激勵的方式為施加集中力，進口和出口位置的激勵同相位，激勵頻段范圍為10～300 Hz，振動分析通過諧響應分析實現。

2.2 優化變量

為考察管道系統的動力學特性，對其進行了模態分析。根據管道系統自身的固有屬性將其分為8個區域，每個區域布置一個動力吸振器，通過優化各動力吸振器的布置位置和參數，對支吊架與管道連接位置在一定頻段內的振動水平進行優化。

每個動力吸振器均包含水平自由度和轉動自由度，優化變量包括：動力吸振器的布置位置、平動剛度、轉動剛度、質量和轉動慣量。動力吸振器參數的上下界見表1，其中動力吸振器的安裝位置采用歸一化坐標，0表示每個區域的起點，1表示每個區域的終點。有限元模型見圖1所示。

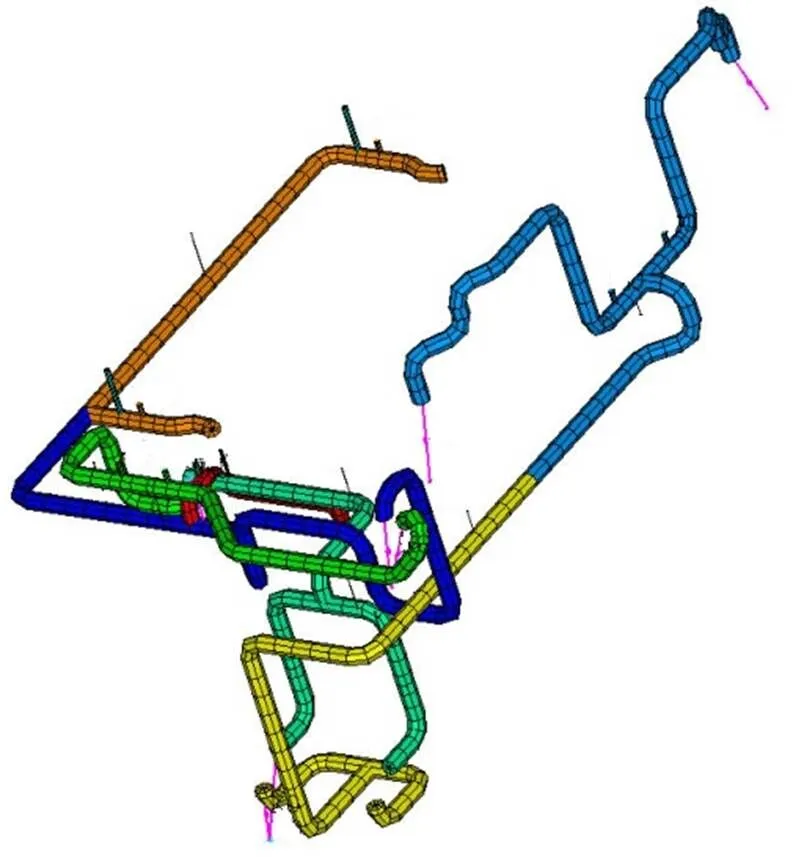
圖1 管道系統有限元模型

表1 動力吸振器參數取值范圍

3 試驗設計

3.1 參數采樣

管道系統布置8動力吸振器，共有40個優化參數，17支吊架約束位置的振動響應為優化目標。不同輸入參數對優化目標影響程度不同，且輸入參數之間也彼此制約，在優化分析時需要重點關注主要設計參數。為定性考察輸入參數與優化目標的變化趨勢指導后續優化策略，在進行優化分析前，對動力吸振器的輸入參數進行采樣。

為避免出現數據截尾，確保樣本點盡可能覆蓋整個分布區間，提高抽樣效率。基于拉丁超立方體抽樣方法，依據各輸入參數的分布函數和定義域范圍，采用等概率分層取樣的方法產生各參數的隨機樣本[4]。對動力吸振器的輸入參數進行采樣，樣本點個數400，隨機種子數69。通過對管道系統有限元模型進行諧響應計算，得出樣本點的真實響應值，并將得到的樣本及其響應值保存在樣本點數據庫中。

通過建立動力吸振器輸入參數到管道支承位置振動響應的輸入輸出關系，可以考察不同輸出位置的振動響應分布。圖2給出了管道與7#支吊架、2#支吊架連接位置輸出振動響應的統計分布，其中振動加速度級基于響應最大值進行了歸一化處理。可以看出，相對于2#支吊架與管道連接位置，7#支吊架與管道連接位置振動響應分布相對緊湊。

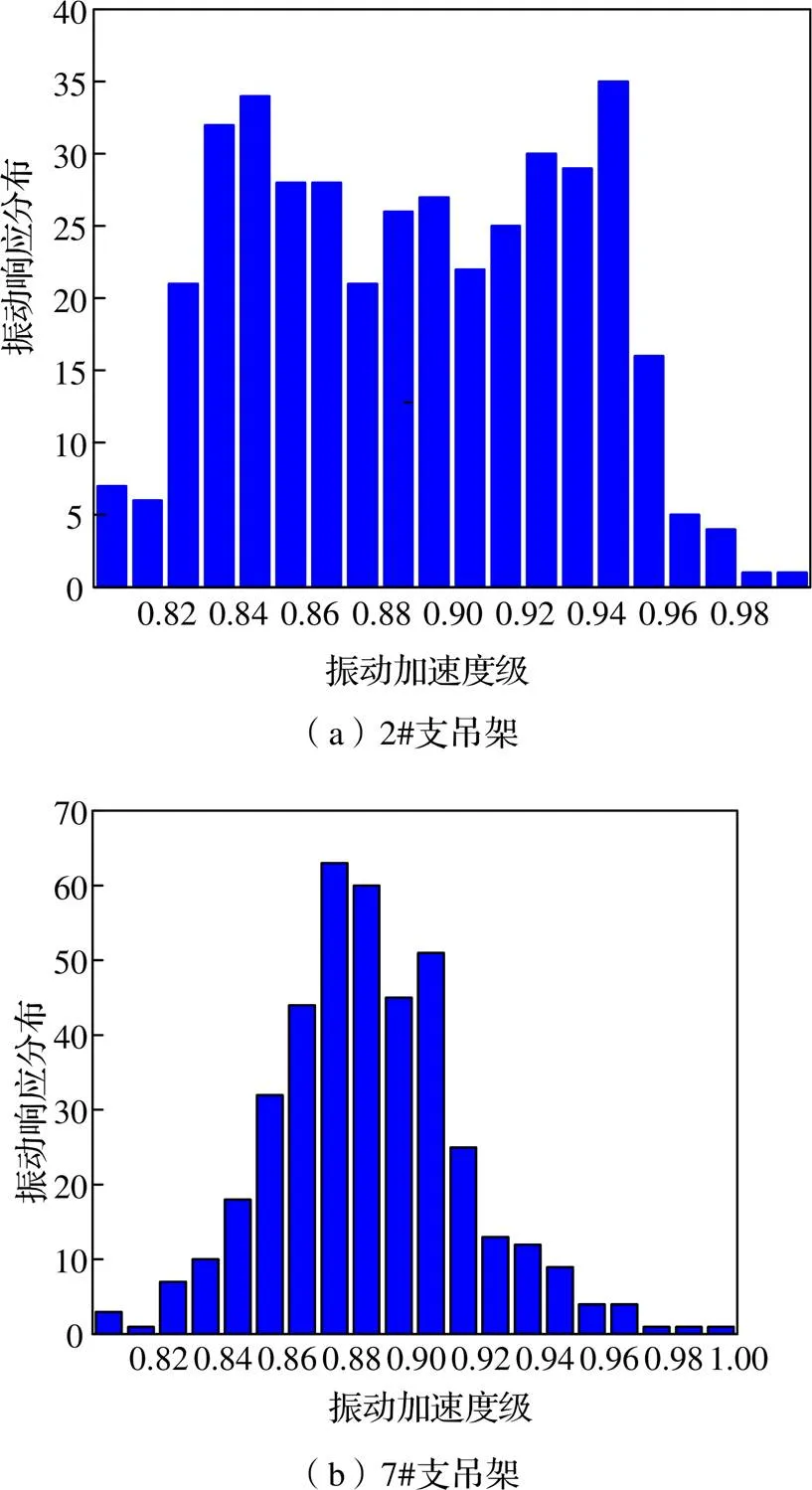
圖2 支吊架位置振動響應統計分布

3.2 代理模型

Kriging模型以變異函數理論為基礎，對有限區域內的變量進行無偏最優估計，其數學模型如下[5-7]：

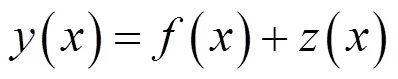
式中：()為待擬合的函數；()為已知的多項式函數；()為一個均值為0、方差為2的隨機函數，表示局部偏差，其協方差矩陣為：

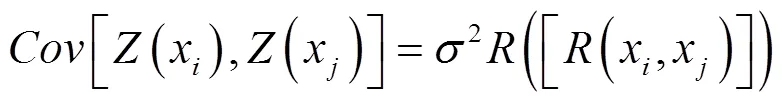
(x,x)為任意兩個樣本點x、x的相關函數，表示其局部偏離程度，形式為：

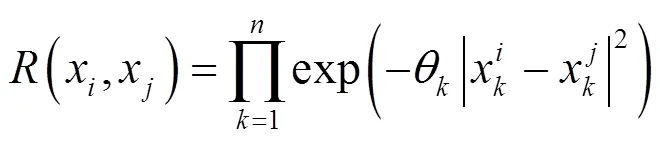
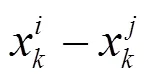
對于任一預測點，其預測值為：

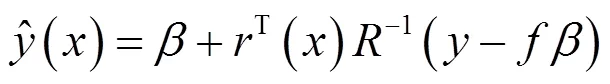
T()表示觀測點于樣本點之間的相關性，形式為：

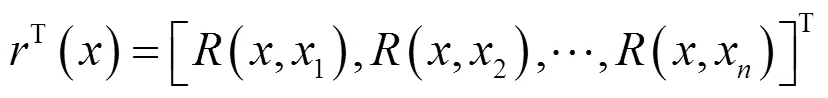
的估計為：

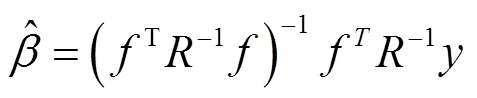
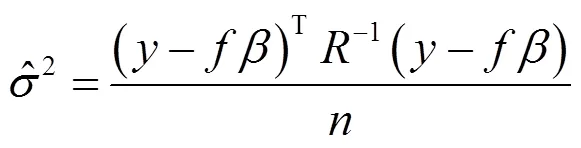
參數θ為極大似然估計，通過求解以下最優化問題得到：

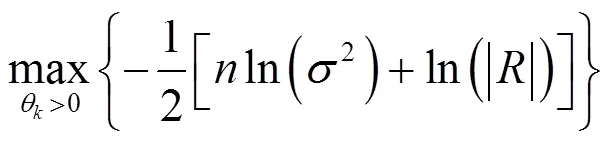
通過求解式（18）求出θ，代入式（15）得到T()，再結合式（14）可以得到最優擬合的Kriging模型。

基于拉丁超立方體采樣計算得到的樣本數據對，采用Kriging插值法建立輸入輸出關系的代理模型。各支吊架位置振動響應代理模型的精度見表2，其定義如下：

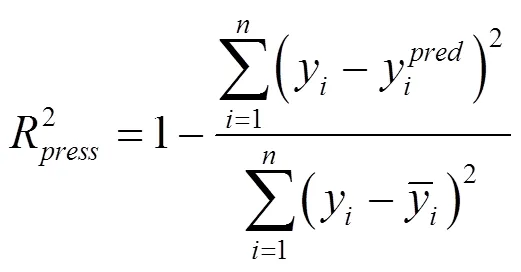
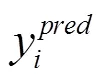
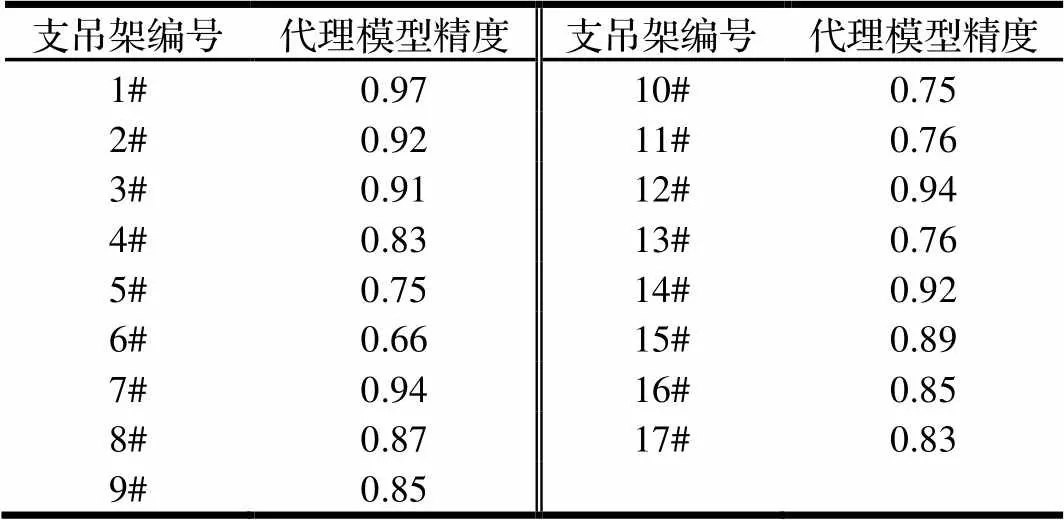
表2 支吊架位置振動響應代理模型精度

由表2中可以看到，代理模型的最高精度可以達到0.97，絕大多數的模型精度在0.7以上，最低為0.66。圖3給出了5#動力吸振器的安裝位置、平動剛度與10#支吊架位置振動響應關系的代理模型。

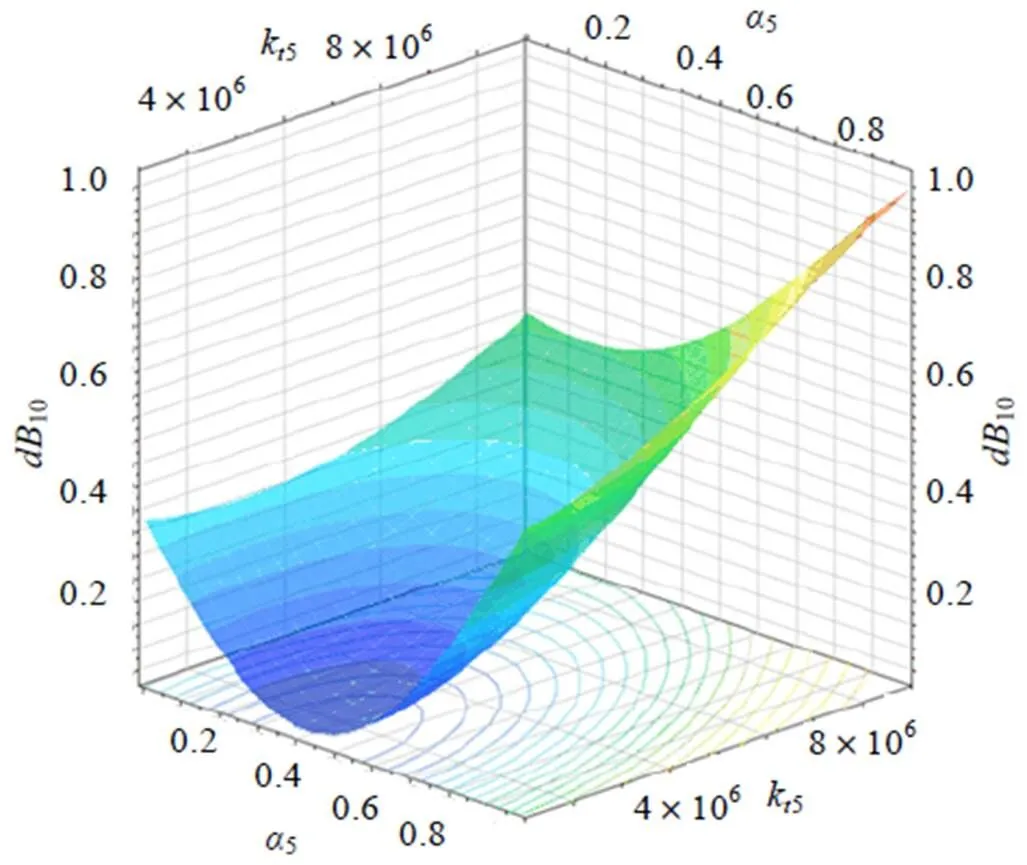
圖3 Kriging擬合的10#支吊架響應代理模型

3.3 相關性分析

通過參數采樣建立的輸入參數與優化目標之間的統計分布，只能定性考察二者之間變化趨勢。對此，對每一組輸入輸出關系進行相關性分析來研究二者的關聯，考察不同參數間的敏度大小。在優化分析時根據輸入參數與優化目標的相關性，可以對輸入參數進行適當縮并。

相關性系數的定義為[8]：

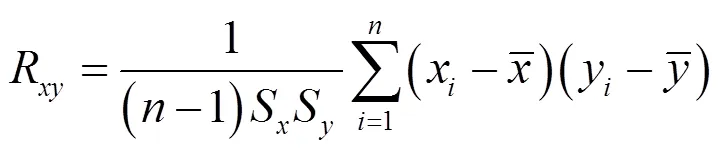
式中：S、S分別為、的標準差。

通過考察輸入變量對系統輸出響應的相關性，可以得到對優化目標影響最顯著的輸入參數。表3給出了1#動力吸振器參數與17個支吊架位置響應之間的相關性系數。

根據表3中的相關性系數可看到，1#動力吸振器對1#、2#、3#支吊架位置的輸出響應影響最明顯，且主要體現在1#動力吸振器的安裝位置、質量、平動剛度三個參數。在第1段管道上布置含平動剛度的動力吸振器，通過調諧其安裝位置、平動剛度、和質量，可有效控制1#支吊位置的振動響應，并對2#、3#支吊架位置的振動抑制起到一定作用。1#動力吸振器對其他支吊架位置的輸出響應相關性較弱。

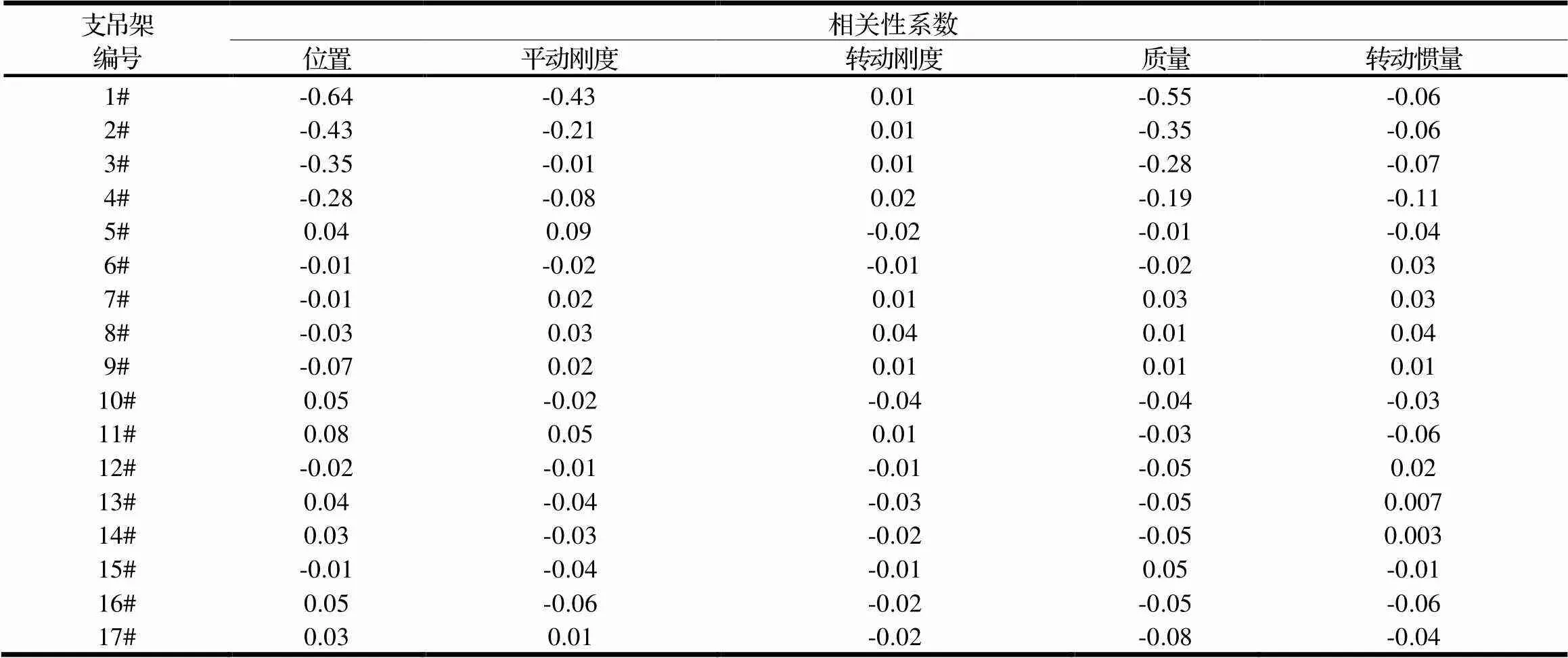
表3 1#動力吸振器參數對振動響應的相關性系數

通過對所有8個動力吸振器的輸入參數分別與17個優化目標之間的相關性進行分析，可知動力吸振器對相近支吊架位置的輸出有較大影響，且間隔2個支吊架之后其影響可以忽略。輸入參數與輸出響應的相關系數都較小，表現出較弱的線性關系。對于任何一個輸入變量而言，至少對一個優化目標有著比較大的影響（線性或非線性），因此，后續優化過程中考慮所有的設計變量，以此盡可能提高優化效果。

4 優化設計

利用數學模型來表征系統輸入輸出之間的關系，通過所構建代理模型代替實際的系統仿真分析進行優化設計，可有效提高優化效率[9-11]。

采用全局高效響應面算法（EGO）對管道上動力吸振器的布置參數進行多目標優化[12-13]。以17個支吊架位置振動響應為優化目標，8個動力吸振器參數為約束條件，可以得到優化問題定義為：

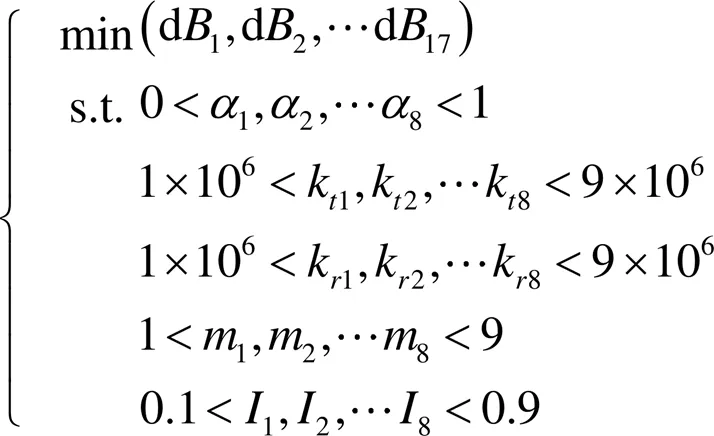
式中：dB為第個支吊架位置的振動響應加速度級；k為第個動力吸振器的平動剛度，N/m；k為第個動力吸振器的轉動剛度，N·m/rad；m為第個動力吸振器的質量，kg；I為第個動力吸振器的轉動慣量，kg·m2。

首先基于代理模型進行尋優，由于不需要重復調用有限元模型計算，進而可以大幅減小求解時間。雖然上述代理模型整體精度較高，但僅基于代理模型進行優化設計得到的最優設計方案，往往與實際情況有較大的偏差。因此，還需將通過代理模型得到的最優解作為輸入參數帶入有限元模型進行驗證。如果代理模型和有限元模型計算得到的輸出響應相差較大，則利用有限元模型的數據對代理模型進行更新。往復以上迭代過程，直至得到最優設計方案，EGO算法流程圖如圖4所示。

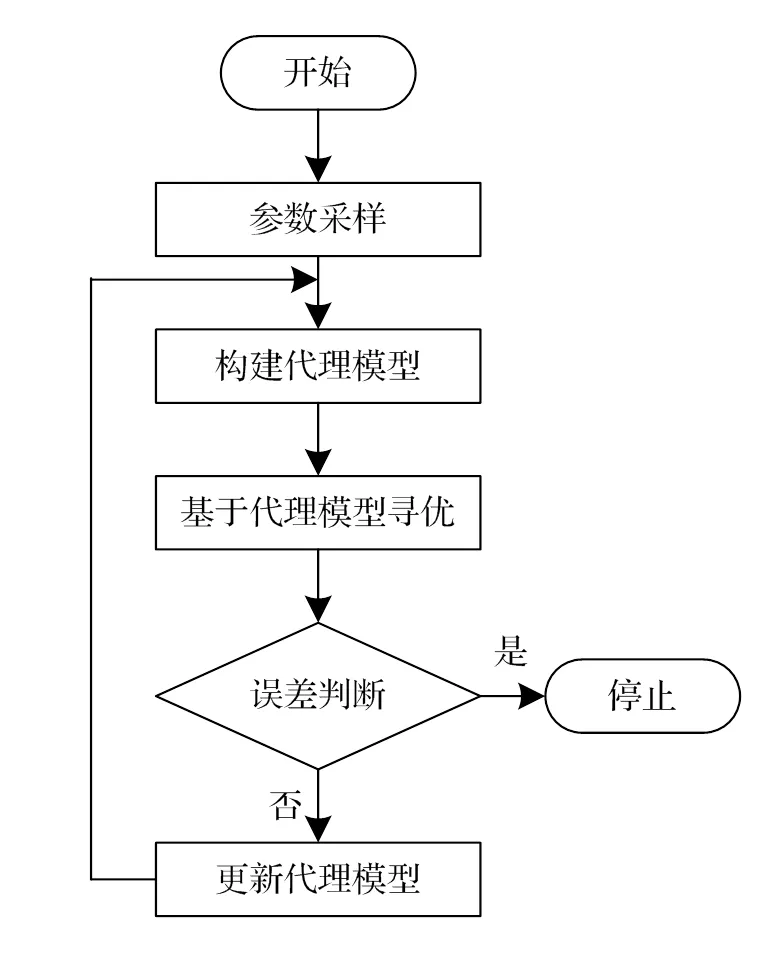
圖4 EGO算法流程圖

利用EGO全局高效響應面算法，經過581次迭代計算（有限元模型計算181次，其中前400次直接讀取代理模型結果）得到最優設計方案。輸入參數見表4，優化前后輸出結果對比見圖5。可以看出17個支吊架位置的振動響應都有不同程度的減小。

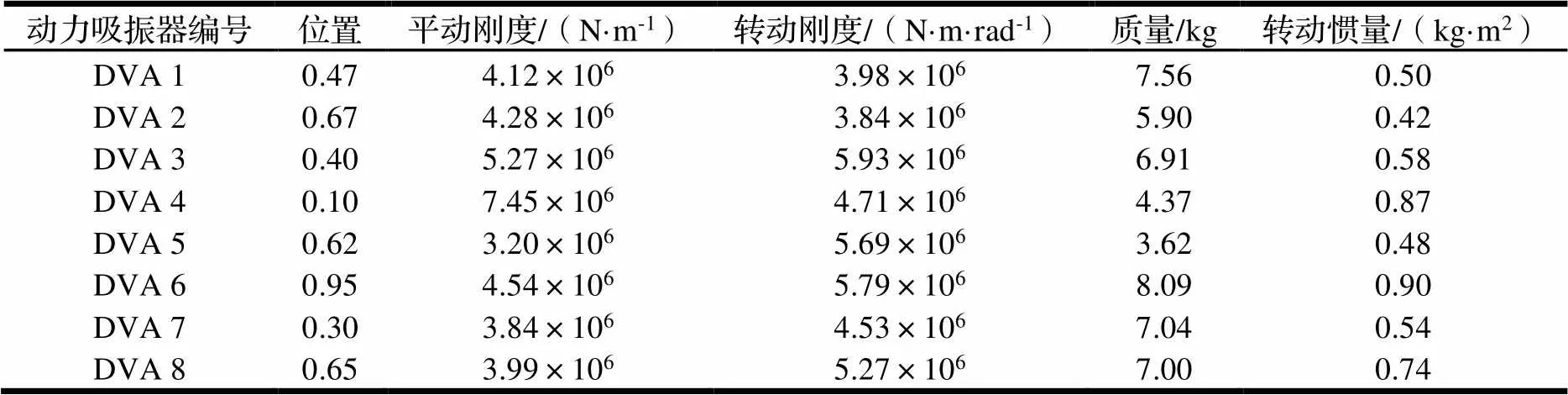
表4 優化后的輸入參數

5 穩健性評估

數值仿真得到的最優解是名義值，由于工程應用中存在制造和安裝的誤差，致使動力吸振器實際的參數與名義值存在一定的偏差。為了避免在確定性仿真中有效的設計可能在實際應用中導致有缺陷的產品，必須考慮設計變量的可靠性[14-15]。

因此，針對得到的最優設計方案進行穩健性評估，考查各輸入參數在設計方案名義值附近±10%擾動時，輸出對輸入變異性的敏感性。假設各輸入參數服從正態分布，采用Monte Carlo抽樣方法進行采樣。

樣本點個數設定為10000，對多目標最優解的魯棒性進行檢驗，評估過程基于代理模型完成。Monte Carlo方法隨機選擇給定分布的參數組合進行多次仿真。

絕大多數輸出變量的標準差在0.1～0.6范圍內，僅有14#、15#支吊架位置超出該范圍，分別為1.87、0.75。即便如此，兩個位置的變異系數也僅分別為2.18%、0.94%，從工程的角度而言一般是可以接受的。圖6給出了管道與15#支吊架連接位置輸出振動響應的統計分布。

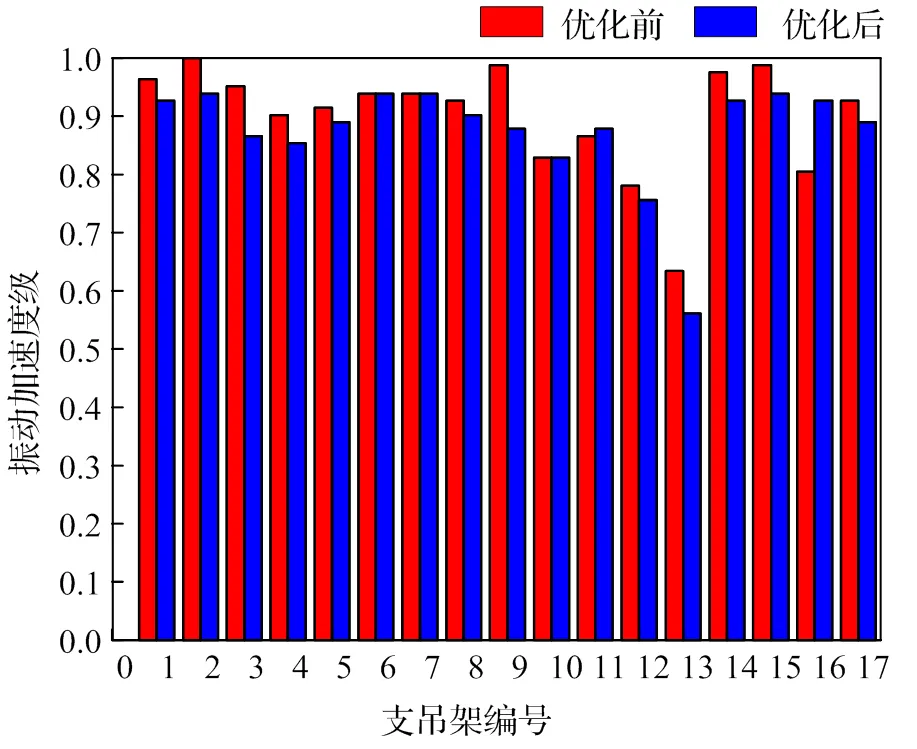
圖5 優化結果對比

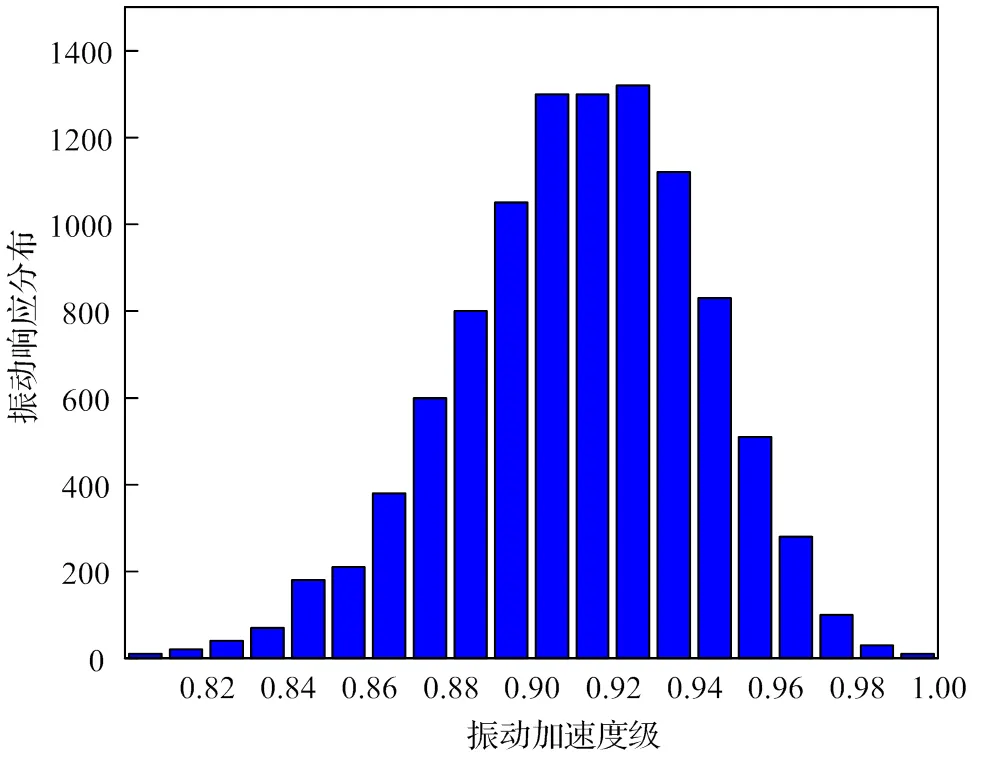
圖6 15#支吊架振動響應統計分布

6 結論

本文以某管道系統為研究對象，通過布置含平動和轉動自由度的動力吸振器，開展簡諧激勵下的振動控制研究。首先通過分層抽樣的方法對輸入參數進行采樣，建立了從動力吸振器布置參數到管道支吊架位置振動響應的輸入輸出關系。基于采樣數據建立了輸入輸出關系的代理模型，并進行了參數相關性分析，考察了系統響應隨各輸入參數變化的規律。采用全局高效響應面算法對動力吸振器的布置參數進行了優化，得到了最優解，實現了低頻段內管道系統的振動被動控制，并考察了最優設計方案優化方案的魯棒性。

[1]余棟棟，何立東，冀沛堯. 阻尼減振技術在管道上應用研究[J]. 噪聲與振動控制，2017，37（6）：186-189.

[2]楊愷，張針粒. 基于反共振原理的管道吸振器調諧方法[J]. 振動與噪聲控制，2017，37（5）：55-60.

[3]熊夫睿，葉獻輝，馮志鵬. 非均勻梁結構減振降噪吸振裝置的多目標優化設計[J]. 噪聲與振動控制，2017，37（6）：199-205.

[4]Yu H，Chung C Y，Wong K P，et al． Probabilistic load flow evaluation with hybrid Latin hypercube sampling and Cholesky decomposition [J]．IEEE Transactions on Power Systems，2009，24（2）：661-667.

[5]韓忠華. Kriging模型及代理優化算法研究進展[J]. 航空學報，2016，37（11）：3197-3225.

[6]Enrica，Bernardini，Seymour，M.J. Spence，Daniel，Wei，et al. Aerodynamic shape optimization of civil structures: A CFD-enabled Kriging-based approach[J] J. Wind Eng. Ind. Aerodyn.，2015（144）：154-164.

[7]Freier L，Wiechert W，Von Lieres E. Kriging with trend functions nonlinear in their parameters: Theory and application in enzyme kinetics [J]. Engineering in Life Sciences，2017，17（8）：916-922.

[8]盛驟. 概率論與數理統計[M]. 3版. 北京：高等教育出版社，2001.

[9]李堅. 代理模型近似技術研究及其在結構可靠度分析中的應用[D]. 上海：上海交通大學，2013.

[10]Jiandong Zhou，M. Hatami，Dongxing Song，et al. Design of microchannel heat sink with wavy channel and its time-efficient optimization with combined RSM and FVM methods[J]. International Journal of Heat and Mass Transfer，2016（103）：715-724.

[11]R. Soundararajan，A. Ramesh，N. Mohanraj，et al. An investigation of material removal rate and surface roughness of squeeze casted A413 alloy on WEDM by multi response optimization using RSM[J]. Journal of Alloys & Compounds，2016（685）：533-545.

[12]Jeong S，Obayashi S. Efficient Global Optimization （EGO） for Multi-Objective Problem and Data Mining[C] IEEE Congress on Evolutionary Computation，2005.

[13]Jones D R. A Taxonomy of global optimization methods based on response surfaces[J]. Journal of Global Optimization，2001，21（4）：345-383.

[14]高偉釗，莫旭輝，付銳，等. 基于Kriging的泡沫填充錐形薄壁結構耐撞性6σ穩健性優化設計[J]. 固體力學學報，2012，33（4）：370-378．

[15]孫光永，李光耀，張勇，等. 基于魯棒性的概率優化設計在薄壁構件耐撞性中的應用[J]. 中國機械工程學報，2007，18（4）： 479-483.

Multi-objective Optimal Design of Dynamic Vibration Absorber for Vibration Reduction of Piping System

WANG Bihao，XIONG Furui，HUANG Qian，ZHANG Wenzheng

(Science and Technology on Reactor System Design Technology Laboratory, Nuclear Power Institute of China, Chengdu 610213, China)

The dynamic vibration absorber (DVA) is known for its capability on reducing pipe vibration under specific frequencies, which is a significant characteristic of vibration of pipeline system in industrial equipment. A type of dynamic vibration absorber (DVA) with translational and rotational degree of freedoms (DOFs) is introduced for reducing pipe vibration under specific frequencies. First of all, the piping system is modeled with beam elements and DVAs is modeled with mass-spring elements. In this model, kinematic equations of DVAs are coupled with the beams. Then, Latin Hypercube Sampling (LHS) technique is applied to sample data points and the input-output relationship that characterizes the mapping from parameters of DVAs to vibration response is established. The surrogate model is constructed based on the points. Kriging interpolation is applied for the data-driven model. The optimization is achieved via Efficient Global Optimization (EGO) algorithm to fine tune the deployment strategy with maximum vibration reduction at several locations. The optimization variables include the location of vibrations absorbers and stiffness parameters. The robustness of the obtained optimal design scheme is evaluated to examine the influence of each design parameter on each output variable when it is disturbed.

multi-objective optimization；dynamic vibration absorber；surrogate model；vibration and noise reduction；correlation analysis

TB 535.1

A

10.3969/j.issn.1006-0316.2020.06.002

1006－0316 (2020) 06－0010－08

2020－02－18

國家自然科學基金項目（51606180；11872060）

王碧浩（1988－），男，四川巴中人，碩士研究生，工程師，主要研究方向為反應堆結構力學分析和優化，E-mail：wangbhao@126.com。