基于響應面的碼垛機器人承載體多目標優化

劉光輝，殷鳴，尹湘云，殷國富

基于響應面的碼垛機器人承載體多目標優化

劉光輝，殷鳴*，尹湘云，殷國富

（四川大學 機械工程學院，四川 成都 610065）

針對4自由度碼垛機器人承載體結構輕量化設計的需要，在對碼垛機器人腕部旋轉部分結構設計和受力體末端執行器承載體動態性能分析的基礎上，建立了一種將多目標優化和響應面優化相結合的優化算法，以承載體的尺寸作為設計變量，以承載體的剛度、強度、一階頻率、質量最輕為優化目標進行優化設計，優化的結果表明：優化后的質量的到明顯減少，一階固有頻率有所提高，變形量有所減小，強度有所增大，但不影響其性能，達到輕量化的優化效果。

碼垛機器人；輕量化；多目標優化；響應面優化

在碼垛機器人研究中，各部分結構的設計直接影響到機器人的性能。輕量化設計作為一個重要的屬性被提出來，通過減少質量或慣量，同時頻率增高、變形量減小、強度提高，提高結構的穩定性能[1]。李錦忠等[2]用有限元和拓撲聯合優化的方法對碼垛及親人整體進行優化。Albert Albers等[3]對機器人胸部進行結構拓撲優化實行輕量化。張大江[4]的多目標對料袋碼垛機器人臂部進行結構優化，賀瑩等[5]利用Box-Behnken和RSM方法建立目標函數和約束函數的RSM模型對碼垛機器人腰部支撐架進行優化設計。建立在這些研究的前提上，本文提出一種多目標與響應面相結合的方法對其腕部進行優化設計。

1 腕部旋轉結構設計

腕部旋轉結構如圖1所示，末端執行器承載體的軸肩通過螺栓固定在腕部支撐座上，承載體主要安裝推力球軸承和旋轉軸，對其起到固定和支撐的作用。其中承載體的內徑＝130 mm，軸肩外徑與軸徑之差2＝40 mm，壁厚1＝40 mm，軸肩2＝15 mm，承載部分1＝10 mm、3＝60 mm。伺服電機安裝在支撐板上面，而減速器對應的安裝在支撐板下面，減速器的末端用聯軸器與旋轉輸出軸連接，帶動軸的旋轉。因為主要承受軸向載荷，故選用推力球軸承與其配合。軸的末端連接法蘭盤，軸的旋轉帶動法蘭盤的旋轉，法蘭盤連接末端執行器，這樣就可以按照要求對物體任意擺放。

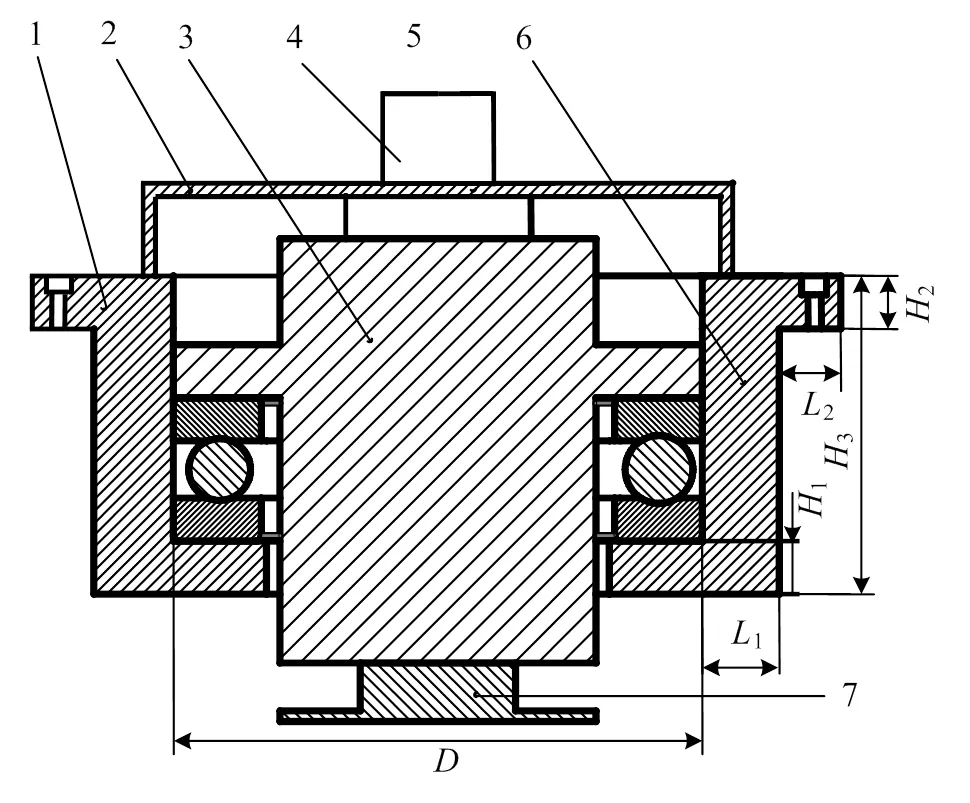
1.末端執行器承載體 2.支撐板 3.旋轉輸出軸 4.伺服電機 5.減速器 6.推力球軸承 7.法蘭盤

2 末端執行器承載體優化

2.1 靜力學分析

承載體上連接著末端執行器且承受著復雜、交變、抓取物等載荷，其動、靜態特性的優劣對機器人的性能具有重要影響，因此剛度、強度和振動穩定性是承載體設計過程中必須考慮的重要指標[6]。為了使模型在實際計算的過程中簡單化并且使分析效率提高，需要對模型進行簡化，承載體去除了其內表面的軸承、轉軸、末端執行器等裝置去掉零件的圓角、螺紋孔倒角等特征，簡化的模型如圖2，承載體所選的材料為45號鋼，質量為13.344 kg，其材料屬性如表1所示。

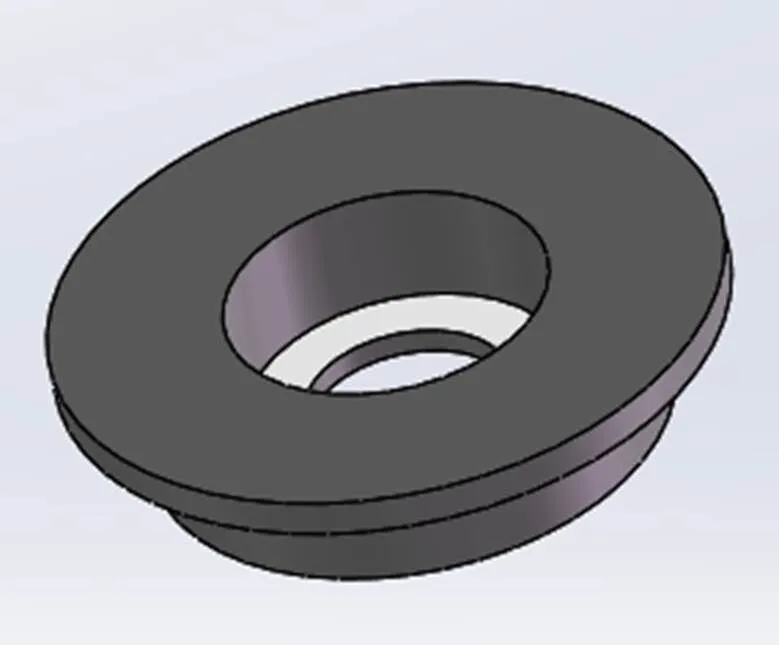
圖2 末端承載體簡化模型

圖3 承載體有限元模型

首先對承載體進行網格劃分，先采用軟件默認的Program Controlled劃分，然后采用Quadratic進一步劃分，為了讓計算更加的準確性采用了Body Sizing。網格劃分單元數：30 092，節點數：46 156。有限元模型如圖3所示。

表1 材料屬性

由于承載體上承載著旋轉軸、軸承、法蘭盤、末端執行器以及抓取的物體等負載，根據實際的要求，通過計算出得知承載體上的總的負載為1000 N。然后在Workbench中施加約束后對圖3的模型進行仿真得出承載體的變形和等效應力如圖4、圖5所示。

圖4 承載體應變圖

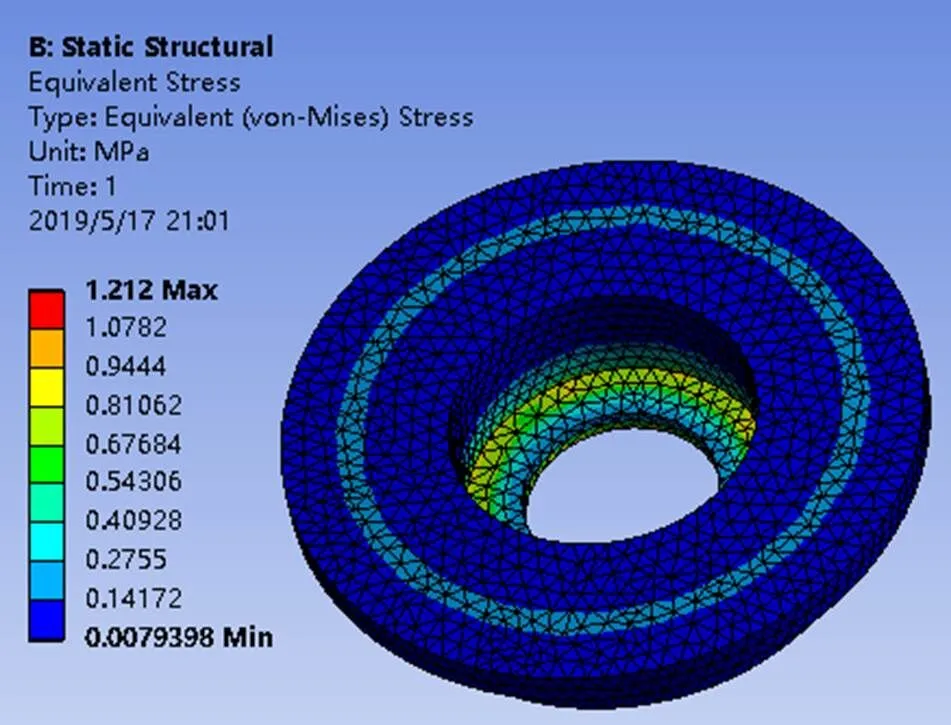
圖5 承載體等效應力圖

從圖5中左邊可以看出：承載體的最大應1.212 MPa，位于臺階外圓邊緣，應該是模型簡化過程中刪除倒角所致。由表1知取45號鋼的屈服強度大于355 MPa，取為355 MPa參考機械設計手冊取許用安全系數[]＝2，計算出許用應力為[]＝177.5 MPa，遠遠大于承載體的最大應力。從圖4右邊可以看出承載體的最大變形為6.3235×10-4mm，變形量很小，發生在臺階內圓邊緣上。綜合以上的結果表明承載體在當前的作用下，強度、剛度都滿足要求，并且還有很大的余量。因此可以考慮從尺寸上優化，在滿足條件的同時，使其質量減輕。

2.2 模態分析

模態分析模態分析是一種常用的研究結構動力特性的一種方法，它可以用來確定系統的振動特性、即結構的頻率和振型[7]。尺寸改變可能帶來固有頻率的改變，如果固有頻率過小，則會與電機轉動引起共振。為了避免共振的發生，結構優化過程中必須要考慮動態特性，因此對承載體進行模態分析。在優化的過程中，頻率的優化也是一個比較重要的約束條件。在靜力學分析的基礎上，加入模態分析，分析出前六階模態如表2所示。

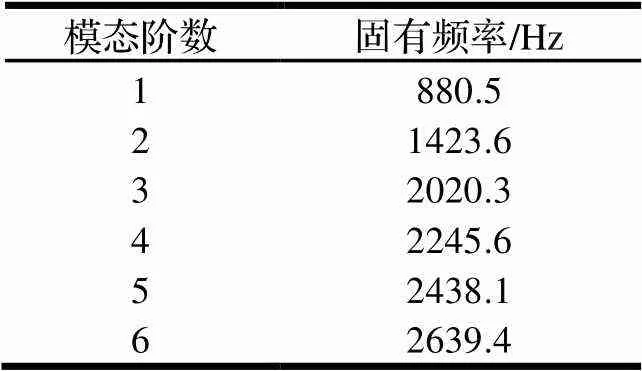
表2 承載體前六階模態

從圖中可以看出承載體的一階固有頻率就達到880.5 Hz，而腕部電機的最高轉速為3000 r/min，其頻率為50 Hz。承載體的固有頻率遠大于轉軸轉動的頻率，因此，承載體的尺寸方面有很大的優化空間。

2.3 承載體多目標優化

從以上的靜力學和模態分析知，該模型可以從尺寸方面進一步優化。承載體結構尺寸的優化采用Workbench中的目標驅動優化模塊，承載體優化采用目標驅動優化與響應面相結合的設計。Design Explorer通過實驗設計DOE和響應曲面Reponse Surface技術來描述設計變量和優化目標之間的關系,通過實驗設計方法產生多種數據，再用設計變量的參數來研究設計變量對優化目標的影響，但因一般輸入設計點數是有限的，所以通過有限個設計點擬合成響應曲面（線）進行研究[8]，最終就可以得到一個較優化的值。

選取以上軸肩外徑與軸徑之差2、壁厚1、軸肩2、內部臺階高度1作為參數的設計變量，以承載體的剛度≤max＝0.0006 mm、強度≤max＝5 MPa為約束條件，以一階頻率要高、質量最輕為優化目標進行優化設計，建立優化的數學模型[9]為：

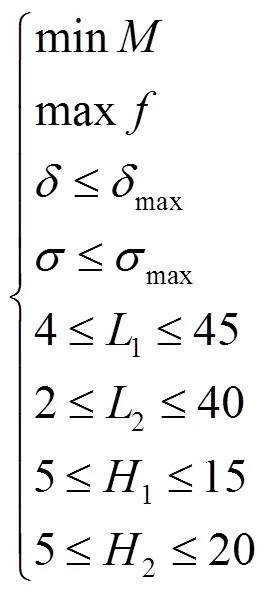
2.3.1響應面法理論

相應面法就是采用一種數學的方法，通過一個近似的表達式來表達出所需要的功能函數，功能函數是通過一定的數據通過線性或二次多項式的形式擬合，得到一個性能值與各數據的響應函數[10]。在實際的計算過程中，經常會用到數學里的多次線性插值，插值函數為：

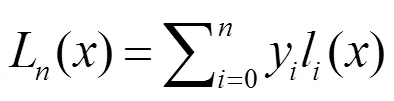
式中：L()為變量的函數；l()為的基函數；y為系數。

首先用多種數據計算得到插值函數L()，然后對設計的變量約束下，得到最優的輸出變量，也就是較優響應結果。

2.3.2響應面優化

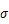
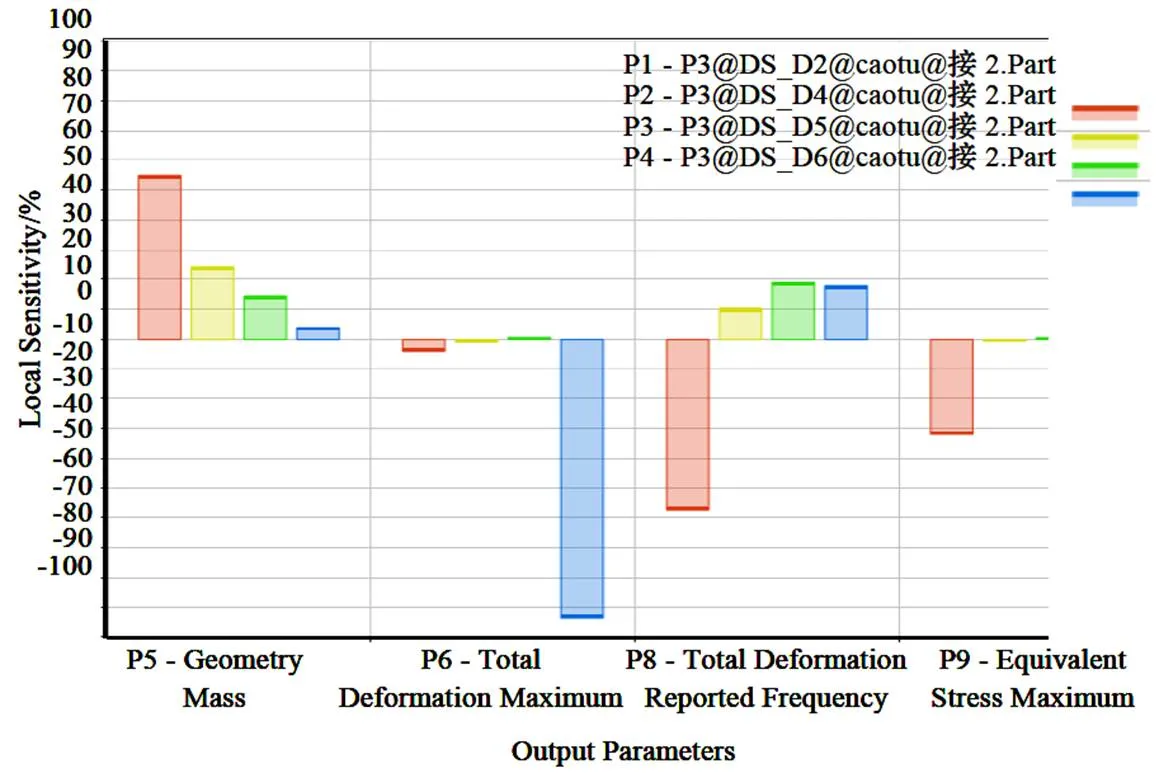
圖6 各參數對輸出結果靈敏度

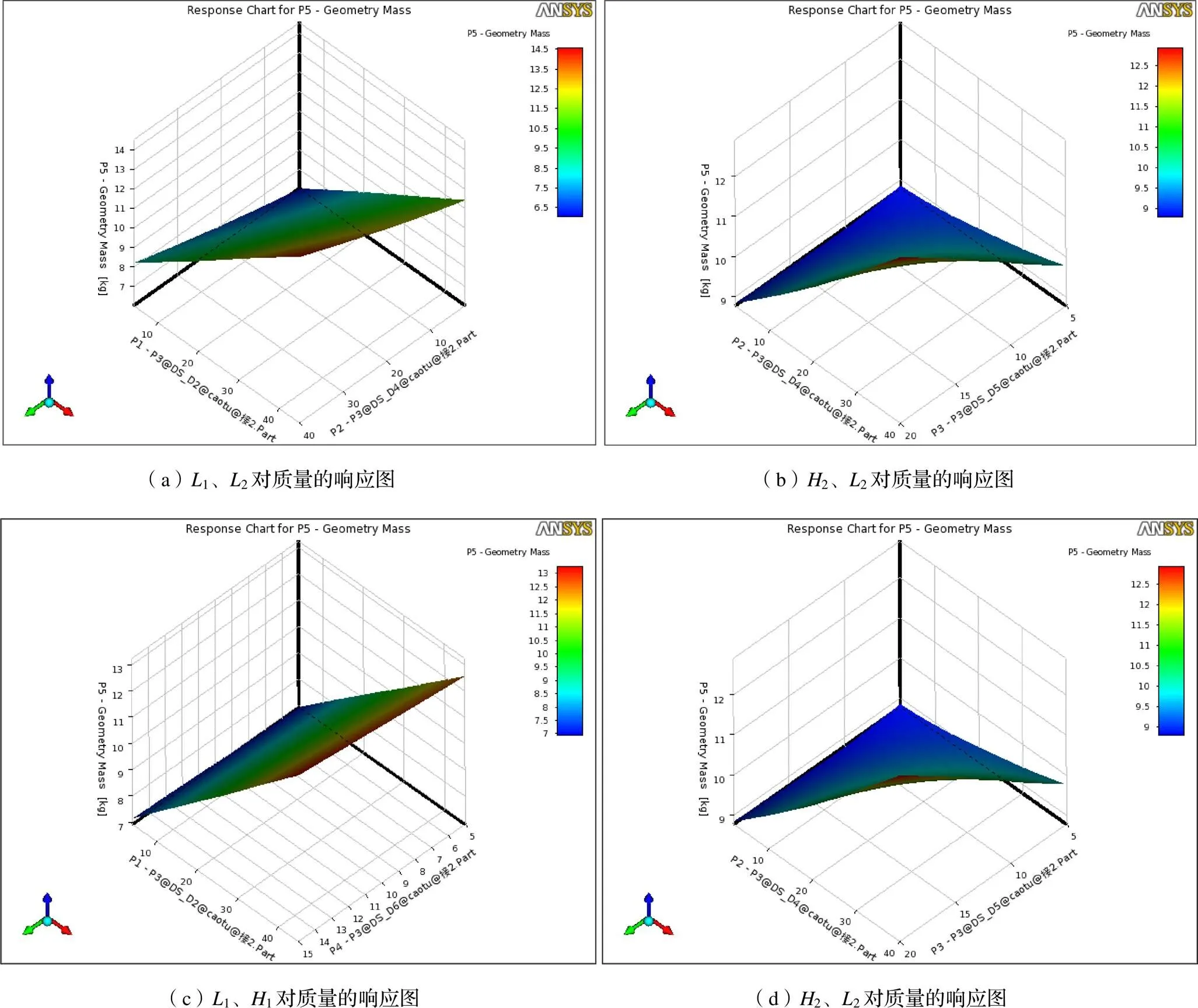
通過響應曲線圖，可以知道哪幾個參數對質量的影響比較大。從以上25組數據中，進一步設定優化目標質量、頻率、變形、應力進行優化，以質量最小、≤max＝0.0006 mm、≤max＝5 MPa為約束條件，建立與四個尺寸的的響應函數進行優化得到下面三組候選數據如表3所示。以質量最小為最先優化目標，選取第一組數據為優化結果，取1＝10 mm、2＝8 mm、2＝7 mm、1＝14 mm導入模型計算對比優化前后的參數如表4所示。

表3 優化結果

表4 優化前后的參數對比

3 結論

（1）完成了腕部旋轉結構的設計，并對相應的結構進行了靜力學、模態分析，分析出來的結果均能滿足設計要求。

（2）在滿足實際要求的情況下，分析結構承載體的結構和工況，確定優化的參數，對結構體進行多目標的優化，運動多目標驅動優化與響應面優化相結合對其結構尺寸進行優化，并得到優化的參數。

（3）優化后的尺寸明顯減小，優化后的質量減少46.7%，變形量減小了，雖然應力增大了，不影響其性能，一階固有頻率有所增大。

[1]王春華，安達，趙東輝. 工業機器人臂部靜動態多目標拓撲優化設計研究[J]. 機械科學與技術， 2016，35（2）：241-246.

[2]李錦忠，唐宇存，陸秋龍，等. 有限元和拓撲聯合優化方法及其在機器人結構輕量化設計中的應用[J]. 機械科學與技術，2019（2）：14-16.

[3]Albers A， Ottnad J，Weiler H，et al. Methods for lightweight design of mechanical components in humanoid robots[C]. Ieee-Ras International Conference on Humanoid Robots. IEEE，2008：609-615.

[4]張大江. 料袋碼垛機器人臂部結構優化[D]. 哈爾濱：哈爾濱工業大學，2018.

[5]賀瑩，梅江平，孫玉德，等. MD-1200YJ碼垛機器人腰部支架的多目標結構優化設計[J]. 食品與機械，2018（2）：87-88.

[6]王啟義. 中國機械設計大賽：第三卷 [M]. 南昌：江西科學技術出版社，2002：1421-1422.

[7]呂濤濤，王玲，殷國富，等. 伸縮皮帶運輸機機架在不同工作狀況下的結構仿真分析[J]. 機械，2019（2）：46-50.

[8]黃志新，劉成柱. ANSYS Workbench 14.0超級學習手冊[M]. 北京：人民郵電出版社，2013.

[9]傅旻，林立峰. 鋼板熱處理前標識設備支撐橫梁的強度分析及優化設計[J]. 機械設計與制造，2016（4）：94-97.

[10]宋儼軒，殷鳴，江衛鋒. 基于響應面的帶式輸送機桁架結構截面優化[J]. 煤礦機械，2017（4）：67-70.

Multi-Objective Optimization of Carrier Structure of Palletizing Robot Using Response Surface Methodology

LIU Guanghui，YIN Ming，YIN Xiangyun，YIN Guofu

( School of Mechanical Engineering, Sichuan University, Chengdu 610065, China)

In order to meet the need of lightweight design of the carrier structure of the 4-degree-of-freedom palletizing robot, the paper analyzes the structural design of the rotating part and the dynamic performance of the carrier at the end of the bearing body. The present work addresses an optimization algorithm combining multi-objective optimization with response surface optimization. The size of the carrier is taken as the design variable, and the stiffness, strength, first-order frequencyand massof the carrier are taken as the optimization objectives. The results show that the optimal solution has guaranteed significant weight decreases, raising the first order natural frequency, declining the deformation, and increasing the strength. The performance is not affected, hence the objective of lightweight optimization is achieved.

palletizing robot；lightweight；multi-objective optimization；response-surface optimization

TH16

A

10.3969/j.issn.1006-0316.2020.06.009

1006－0316 (2020) 06－0056－06

2019－10－30

四川省科技計劃項目（2018GZ0111）

劉光輝（1992－），男，湖北孝感人，碩士研究生，主要研究方向為智能制造。

殷鳴（1987－），男，四川成都人，博士，副教授，主要研究方向為增材制造技術和智能制造，E-mail：mingyin@scu.edu.cn。