基于云粒子群優化神經網絡的損傷識別算法研究

◎崔寶影 程權成

（遼寧機電職業技術學院華孚儀表學院，遼寧丹東118009）

橋梁結構損傷識別對于預測橋梁健康狀況具有重要作用，為避免經濟損失和人員傷亡，工程人員將以此為依據做出重要決策。目前存在大量關于損傷識別因子的研究，如采用模態振型[1]、類柔度差曲率和頻率攝動[2]、結構響應向量（SRV）[3]、應變響應統計信息[4]、剛度法[5]、曲率模態變化率[7]等作為損傷識別因子進行橋梁結構損傷識別。隨著人工智能算法的成熟，越來越多的研究員將其應用于結構損傷識別，如李雪松等人利用卷積神經網絡研究了混合噪聲模式下的結構損傷識別[6]；胡倩利用人工神經網絡進行結構損傷識別，同時采用貝葉斯正則化（BR）的Levenberg Marquardt（LM）算法訓練前饋神經網絡[8]；邢哲等人采用二階段的RBF損傷識別方法[9]；占洋洋等人研究了大量以神經網絡為基礎的結構損傷識別算法[10]；蘭翔研究了不同損傷狀況和噪聲情況下以加速度為識別因子的結構損傷識別方法[11]；何睿等人針對僅采用BP神經網絡識別損傷容易陷入局部最優的問題，結合混沌粒子群算法進行優化并完成結構損傷識別研究[12]；同樣，許如鋒等人結合粒子群算法通過改善BPNN權值閾值的方法進行橋梁結構損傷識別[13]。

筆者針對BPNN初始權值閾值設置不當容易達不到全局最優的特點，研究了云理論-粒子群-BPNN（云粒子群優化神經網絡）的算法，然后將其應用于識別結構損傷。以某實際橋梁為研究對象，利用ANSYS軟件建立有限元模型，并通過降低彈性模量的方法獲得非噪聲影響下靜力應變數據作為損傷識別因子從而構成樣本庫。最后基于此樣本庫訓練云理論-粒子群-BPNN及測試驗證其性能。

1 云粒子群優化神經網絡

1.1 云粒子群優化算法

粒子群算法是一種在多維空間中利用群體搜索最優的智能算法。其算法流程如下：

1.1.1 初始化

初始化搜索空間范圍維數D、群體粒子總數N、迭代終止次數K、粒子n的速度Vn∈[Vmin，Vmax]，粒子 n 的位置 Sn∈[Smin，Smax]。

1.1.2 更新速度和位置

定義適應度函數，根據以下公式更新速度和位置。

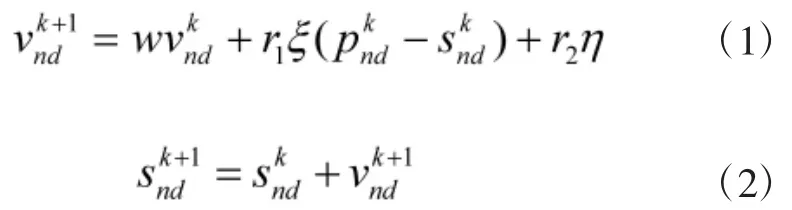
式中，k 為當前迭代次數，k=1，2……K，d=1，2……D，n=1，2……N，Pn=（Pnl，Pn2……PnD為粒子 n最接近目標的坐標，Pg=（Pg1，Pg2……PgD） 為群體最接近目標的坐標。w為慣性權重，通常取0.726；r1和r2為非負常數，稱學習因子，通常取1.49445；ξ和η為偽隨機數，均勻分布在[0,1]區間內。

從上式可以看出慣性權重為固定值顯然不能適應持續搜索的能力，即初期距離最優位置較遠需要較大的慣性權重，后期應自適應的改變權重，因此筆者引入云理論，通過云發生器產生能夠針對不同粒子不同狀況的自適應慣性權重。

云粒子群優化算法的流程如下：

粒子群初始化。同粒子群初始化參數。同時定義適應度函數并計算。

根據以下公式計算慣性權重w，并將得到的w 代入公式（1）和（2）得到 Vn和 Sn，以及更新 Pn和Pg。

慣性權重的設置如下：

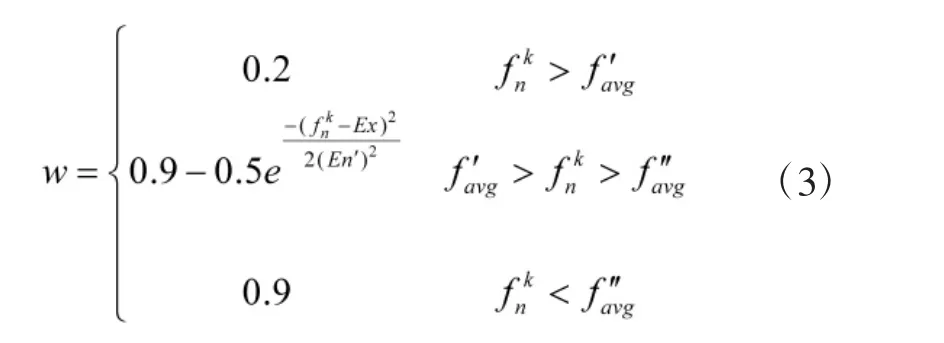
定義fn為粒子n的適應度；fkavg為所有粒子的平均適應度為適應度大于fkavg的所有粒子的平均適應度，f＂avg為適應度小于fkavg的所有粒子的平均適應度；云理論期望值EX=fkbest，fkbest為群體最優適應度；熵值En（f＇avg-fkbest）/c1；超熵 He=En/c2；En＇=normrnd（En,He）,normrnd 為正態隨機數發生器。

返回上一條繼續迭代直到滿足停止條件。

1.2 云粒子群優化BP神經網絡算法

云理論—粒子群—BPNN（云粒子群優化神經網絡）算法的實質是利用云理論優化粒子速度更新權重w，進而優化BPNN的初始權值閾值的過程。因此首先要建立BPNN模型，然后實現云理論—粒子群—BPNN算法，最后利用樣本數據訓練網絡，完成預測。其流程如圖1所示。

2 基于云粒子群優化神經網絡損傷識別算法

2.1 建立有限元模型

筆者圍繞秦皇島某橋梁展開研究，該橋由3聯12跨構成，每跨由六片單箱單室箱梁構成。采用彈性模量 Ec=3.40×104Mpa，泊松比 μ=0.22，密度ρ=2600建立有限元模型，其中主梁用beam188單元、連接主梁的濕接縫采用beam44單元模擬，橋的橫截面如下所示。

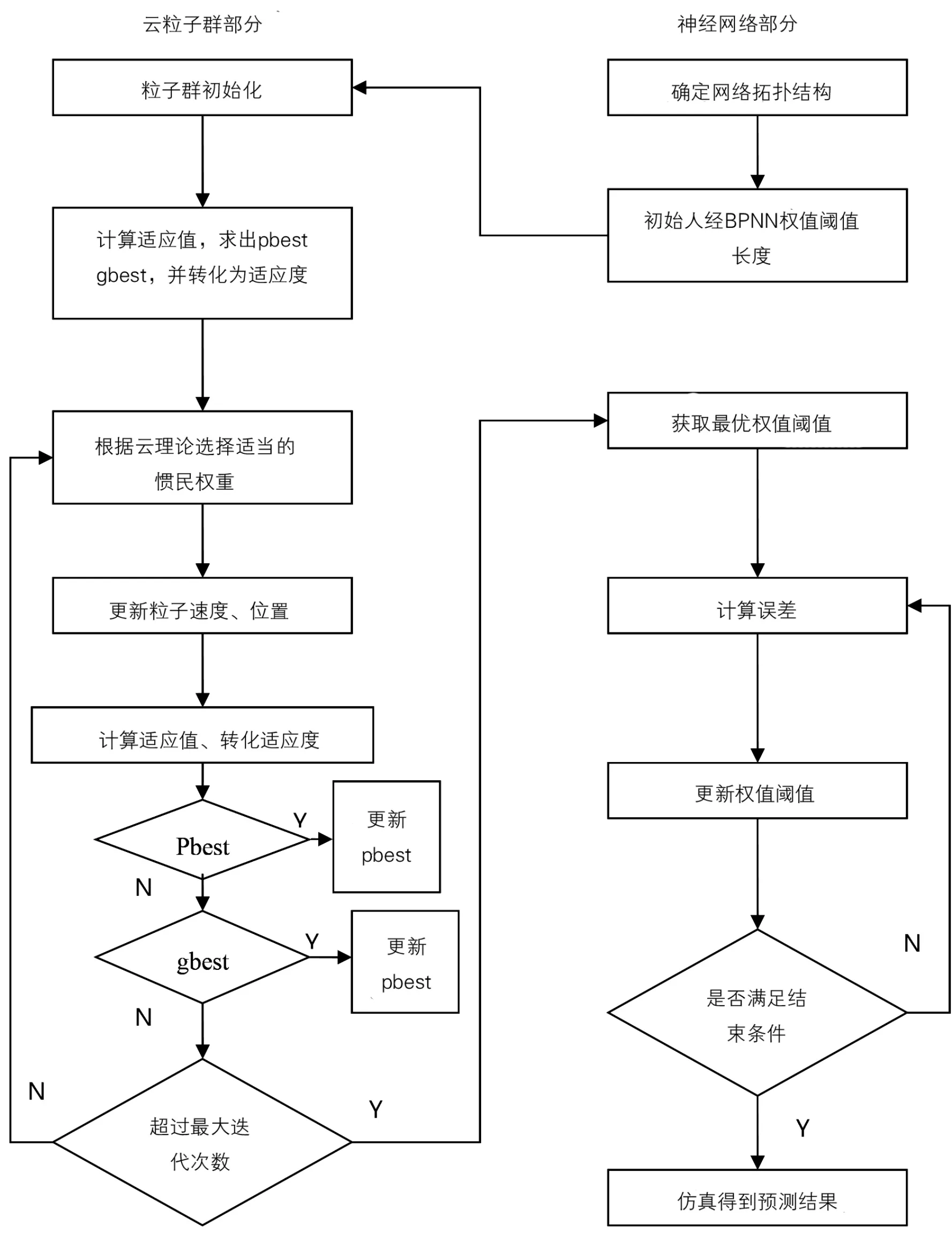
圖1 云粒子群優化神經網絡流程

基于該模型進行有限元分析并結合橋梁傳感器安裝位置以及工程經驗，最終選取以下四個位置作為損傷位置：距橋梁左端0.6米；四分之一跨；跨中；四分之三跨。

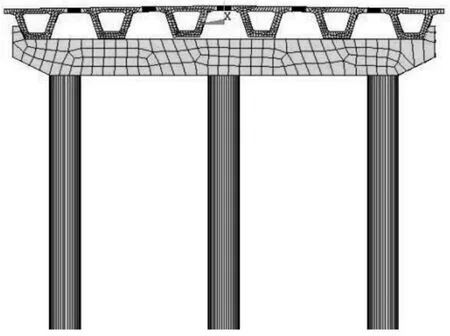
圖2 橋梁有限元模型的橫截面

然后采取分別降低某一損傷位置處的彈性模量的方法獲取14個位置非噪聲影響下的靜力應變數據，并通過公式（1）得到靜力應變變化率構成樣本庫。此處選擇的用于獲取靜力應變數據的14個位置與實際橋梁安裝傳感器的位置一致，其位置如圖3所示。

圖3 獲取靜力應變數據的14個位置所在單元

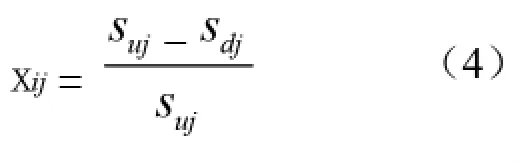
式中，i=1，2……4表示位置i發生損傷，j=1,2……14表示第j個位置單元，Suj和Sdj分別代表未發生損傷和存在損傷時位置單元j的靜力應變數據，Xij表示發生損傷i時位置單元j的靜力應變變化率。

筆者采用二階段損傷識別法，首先采集數據識別損傷位置，若判斷存在損傷，則進一步識別損傷程度。若判斷無損傷，則無須進一步識別損傷程度。

2.2 損傷位置識別

筆者搭建的BP神經網絡（以下簡稱BPNN）模型如圖所示，以靜力應變變化率作為神經網絡的輸入樣本，設置損傷程度為10%、20%、30%、40%狀況下獲得的靜力應變變化率作為訓練樣本，損傷程度為35%和50%狀況下獲得的靜力應變變化率作為測試樣本。

圖4 BP神經網絡的模型

基于以上結構及數據首先利用16組訓練樣本訓練云理論—粒子群—BPNN（CPSO-BPNN）模型，然后將測試樣本輸入訓練后的神經網絡，其輸出結果如表1所示，其CPSO的適應度曲線圖5所示。

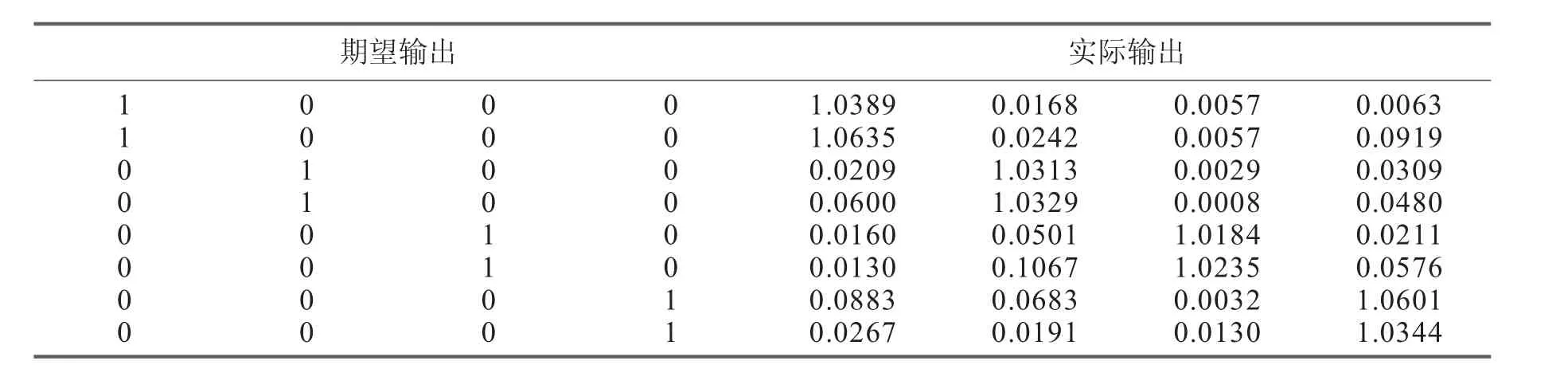
表1 CPSO優化神經網絡測試數據輸出

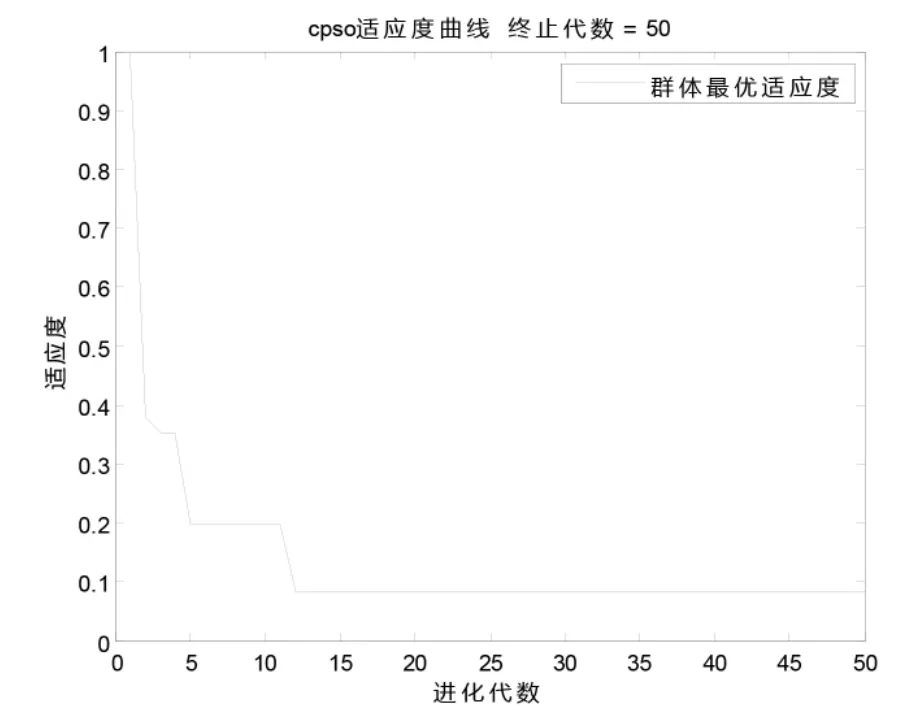
圖5 單位置損傷定位適應度曲線

表中數據表明：測試結果與期望結果完全吻合，說明了基于云理論—粒子群—BPNN算法可以有效地識別損傷位置。

2.3 損傷程度識別

當測試結果表明橋梁結構存在損傷位置，則需要進一步測試其損傷程度。依然采用上述網絡模型，只期望輸出是在相應損傷處顯示損傷程度。首先利用訓練樣本訓練云理論—粒子群—BPNN，然后將測試樣本輸入訓練后的神經網絡，其輸出結果如表2所示。

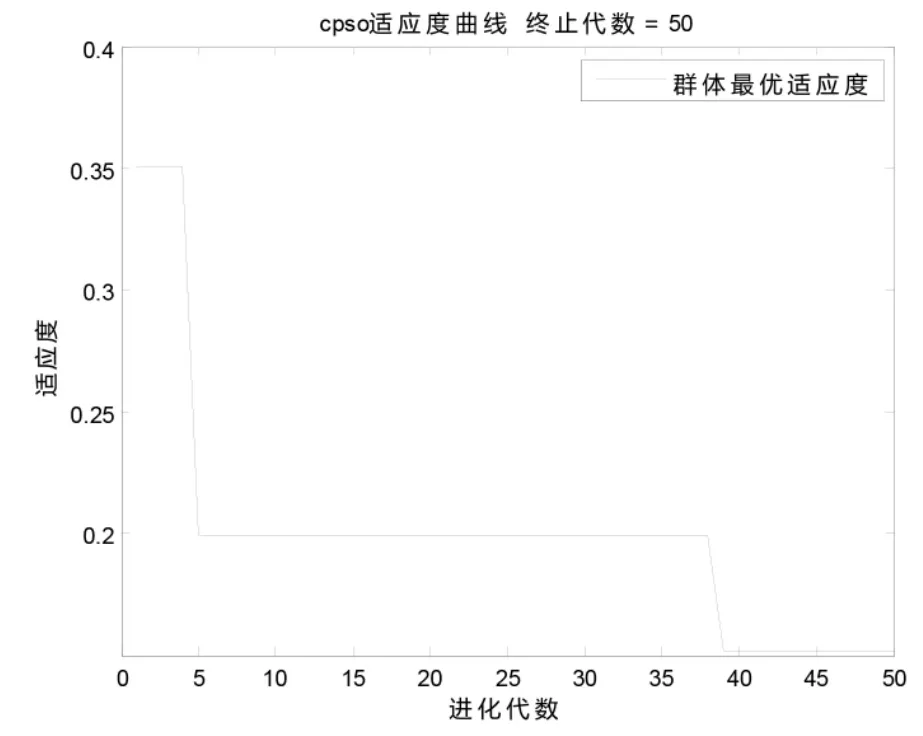
圖6 單位置損傷程度識別的適應度

3 結論

筆者采用識別精度較高的靜力應變數據作為損傷識別因子，以某實際橋梁為研究對象，利用ANSYS軟件建立有限元模型，并通過降低彈性模量的方法獲得非噪聲影響下不同損傷狀況的靜力應變數據構成樣本庫。針對BPNN初始權值閾值設置不當容易達不到全局最優的特點，采用粒子群算法優化BPNN初始權值閾值。進一步地，針對粒子群本身慣性權重為固定值，設置過大容易錯過最優位置，設置過小收斂速度過慢的缺點，利用云理論設置自適應慣性權重，實現云粒子群優化BP神經網絡算法。然后利用樣本庫中的樣本訓練并測試云理論-粒子群-BPNN。仿真實驗可以看出，云理論-粒子群-BPNN算法可以判斷出損傷的位置并進一步判斷其損傷程度。最后經過數十次的實驗，結果表明云理論-粒子群-BPNN算法具有良好的穩定性。筆者的研究數據都在非噪聲影響下獲取的，下一步的研究重點將圍繞噪聲影響下該方法的可行性并做出改進。

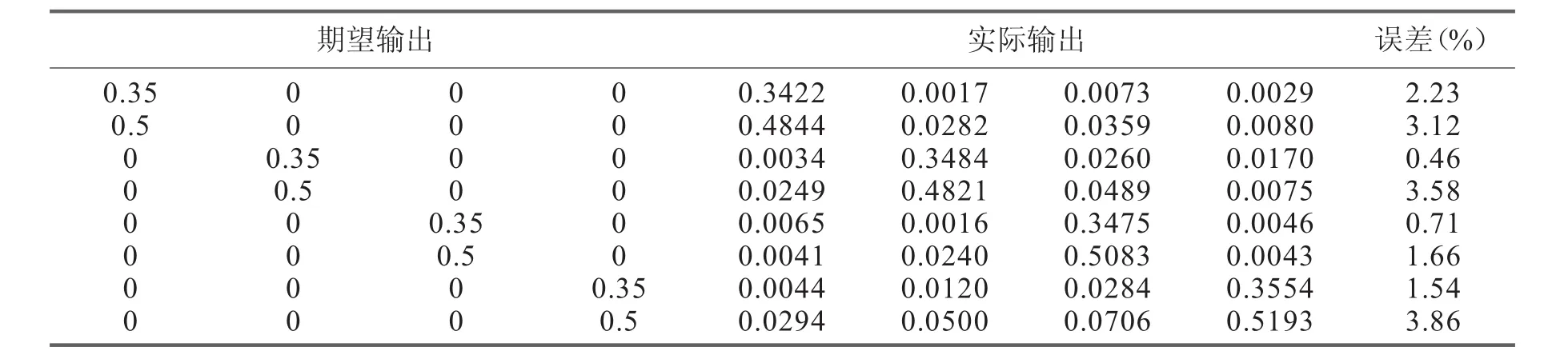
表2 優化神經網絡的測試數據輸出結果