基于小波分析的多層框架結構損傷識別研究

丁 科 ，鄧宇龍 ，肖運蔚

(1. 中南林業科技大學 土木工程學院，長沙 410004；2. 中南林業科技大學 工程流變學湖南省重點實驗室，長沙 410004；3. 湖南建工集團 裝飾工程有限公司，長沙 410004)

隨著時間的推移，大部分結構在使用過程中會出現不同程度的損傷，尤其是一些結構經常在超負荷的情況下服役，造成了構件或部分結構出現損傷﹒縱使在正常使用情況下，隨著服役年限的增加，結構的強度和剛度也會有所下降，當損傷達到一定程度時可導致結構完全破壞﹒因此，及時對結構進行檢測和診斷，確定其損傷出現的位置以及損傷的程度，對于維護和確保結構安全可靠是非常必要的﹒

結構出現損傷的根本原因在于組成結構的構件局部強度或剛度降低和質量損失，其在結構動力特性參數上的表現是結構的模態參數發生了改變﹒因此，可以根據系統的動態特性參數來對結構進行損傷定位﹒通常可以根據頻率、振型、模態應變能、剛度矩陣、柔度矩陣、頻響函數、傳遞函數等參數來定位損傷位置﹒如Cawley[1]曾經利用結構損傷前后頻率的變化來確定損傷位置；Yuen[2]根據結構損傷前后振型與特征值的比值來分析懸臂梁的損傷位置；張勇等[3]認為曲率模態的微分對結構損傷有較高的敏感性；Stutz 等[4]根 據響應面模型和柔度矩陣，運用粒子群優化方法來求解損傷識別逆問題；鄭飛等[5]基于單元模態應變能變化率提出了多位置損傷診斷的組合方法；張龍[6]以塑性率作為損傷參數來分析鋼筋混凝土框架損傷程度﹒

小波變換是在傅立葉變換(Fourier transform)的基礎上發展起來的，克服了其不能作局部分析的不足，廣泛地應用于圖像處理、語音識別、偏微分方程求解、故障診斷等方面﹒近20 年來，利用小波變換對信號奇異性處理的優點，使其被逐步應用到土木工程結構損傷檢測中﹒郭健[7]分析了小波包能量特征提取方法，并通過耦合神經網絡法對損傷特征信息進行融合用以確定損傷位置；管德清等[8]曾對運用小波變換對單層平面框架結構的應變模態進行處理，判斷框架裂縫位置；李洪泉等[9]運用小波變換的尺度函數來判斷結構損傷；Magdalena[10]的研究表明梁高階模態的小波變換對損傷具有較高的敏感性；楊佑發等[11-12]基于構件損傷后固有頻率的一、二階靈敏度矩，通過混合迭代算法識別損傷位置；楊海鳴等[13]根據小波模極大值分布圖來確定結構的損傷位置；鞠彥忠等[14]將小波去噪和小波神經網絡相結合進行框架結構的損傷識別﹒

本文主要考慮運用小波變換對2 層框架結構的曲率模態進行處理，并分析不同工況下其對框架結構損傷的識別能力﹒

1 小波變換基本理論

小波變換是20 世紀80 年代發展起來的一種數據處理工具﹒1981 年法國學者Morlet 基于群論思想首次提出小波分析這一概念并成功運用在地質數據分析，由此引起了其他學者的廣泛關注和研究﹒1985 年，Meyer 提出了光滑的小波正交基；1986 年，Lemarie 在Meyer 的指導下提出了多尺度分析思想；1988 年，Daubechies 提出一系列具有緊支集的光滑正交小波基﹒此后，在Mallat 多分辨分析基礎上形成了快速小波算法，加快了小波變換在實際中的應用﹒

則稱 Ψ (t)為小波母函數﹒引入伸縮和平移因子后，小波母函數 Ψ (t)可以寫為：

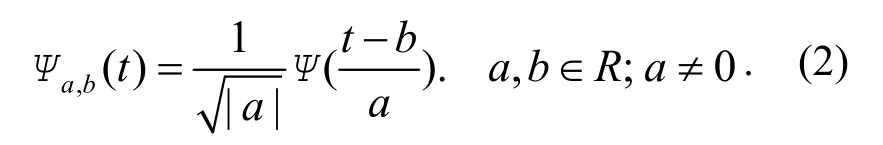
其逆變換為：

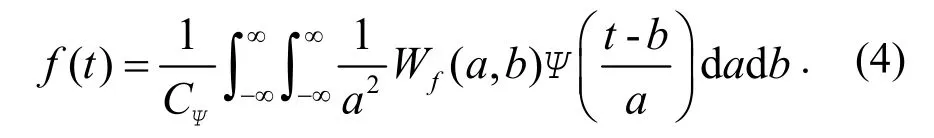
工程中常用于損傷識別的小波函數有：Daubechies 系列小波、Morlet 小波、Symlets 系列小波、Meyer 小波等﹒

2 多層平面框架結構損傷分析

多層平面框架結構作為一個離散的多自由度的系統，其自由振動方程為：

式(6)表示系統無阻尼時的自由振動方程﹒運用有限元分析軟件，可以獲取結構的各階振型；然后根據中心差分公式，可以得到第r 階振型在第i個結點處的模態曲率：

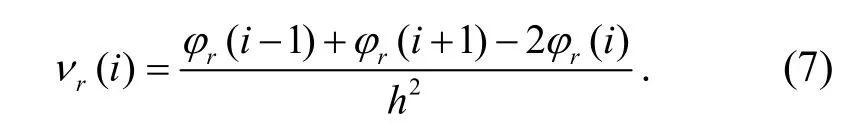
第1 步：運用有限元分析軟件計算模型結構的固有頻率和振型﹒對于實際結構，可以通過儀器測量其前幾階固有頻率和振型﹒

第2 步：根據公式(7)對振型進行計算，得到其模態曲率﹒

第3 步：選擇適當的小波類型和分解層數，運用連續小波變換對模態曲率進行分析，根據變換后的小波分解系數判斷結構的損傷位置﹒

圖1 平面2 層框架結構模型

如圖1 所示，有一2 層平面框架結構，第1 層層高5 m，第2 層層高4 m，跨度為12 m﹒取混凝土強度等級為C25，梁柱橫截面均為矩形，其橫截面寬度 b= 0.2 m ，高度 h= 0.3 m，材料彈性模量 E = 3.1 ×1 04MPa，泊松比 μ = 0.2，密度ρ = 2 500 kg/m3﹒取單元長度為10 mm，采用平面剛架單元對該框架結構進行分析﹒現假設該平面框架結構發生損傷，損傷情況如表1 所示﹒

工況一：左邊立柱AG 距A 點2 m、7 m 處，右邊立柱BH 距B 點6 m 處，橫梁GH 距G 點1 m處，橫梁CD 距C 點9 m 處共5 處發生損傷，損傷情況如表1 所示﹒運用自編的分析軟件，得到其前八階振型，如圖2 所示﹒

表1 框架損傷情況

圖2 工況一下框架結構的振型

根據公式(6)計算各階振型的曲率，基于Matlab 平臺編制程序對各階模態曲率進行連續小波變換，本文的小波函數為db3 小波，分解層數為15 層，圖3 所示為圖2 八階模態的處理結果﹒

由圖3 可以看出，損傷位置處的小波變換系數存在不同程度的模極大值﹒然而，也有部分模態的損傷位置不明顯，如圖3a)中一階模態的小波變換在2#、3#損傷位置不明顯；圖3f)中第六階模態的小波變換在1#損傷位置不明顯﹒故在實際檢測中，需要得到結構的多階模態，綜合考慮各階模態的小波變換系數模極大值﹒

工況二：結構發生2 處損傷，分別為右邊立柱BH 距B 點7 m 處損傷35%，橫梁GH 距G 點3 m 處損傷30%﹒根據公式(6)計算了前八階振型的曲率，然后對各階模態曲率運用db3 小波進行15層小波分解﹒圖4為該平面框架在工況二時前八階模態曲率的小波變換系數﹒由圖4 可知，八階模態的小波變換系數在損傷位置處均存在不同程度的模極大值﹒因此，可以根據小波變換系數確定損傷的位置﹒

工況三：結構發生1 處損傷，為右邊立柱BH距B 點3 m 處，損傷40%﹒運用有限元分析軟件計算其前八階振型后根據(6)式計算其各階振型的曲率，對各階模態曲率采用db3 小波進行10層連續小波分解﹒圖5 為前八階模態曲率的第10層小波變換結果﹒由圖5 可看出，前八階模態曲率的小波變換系數在損傷位置均存在模極大值﹒

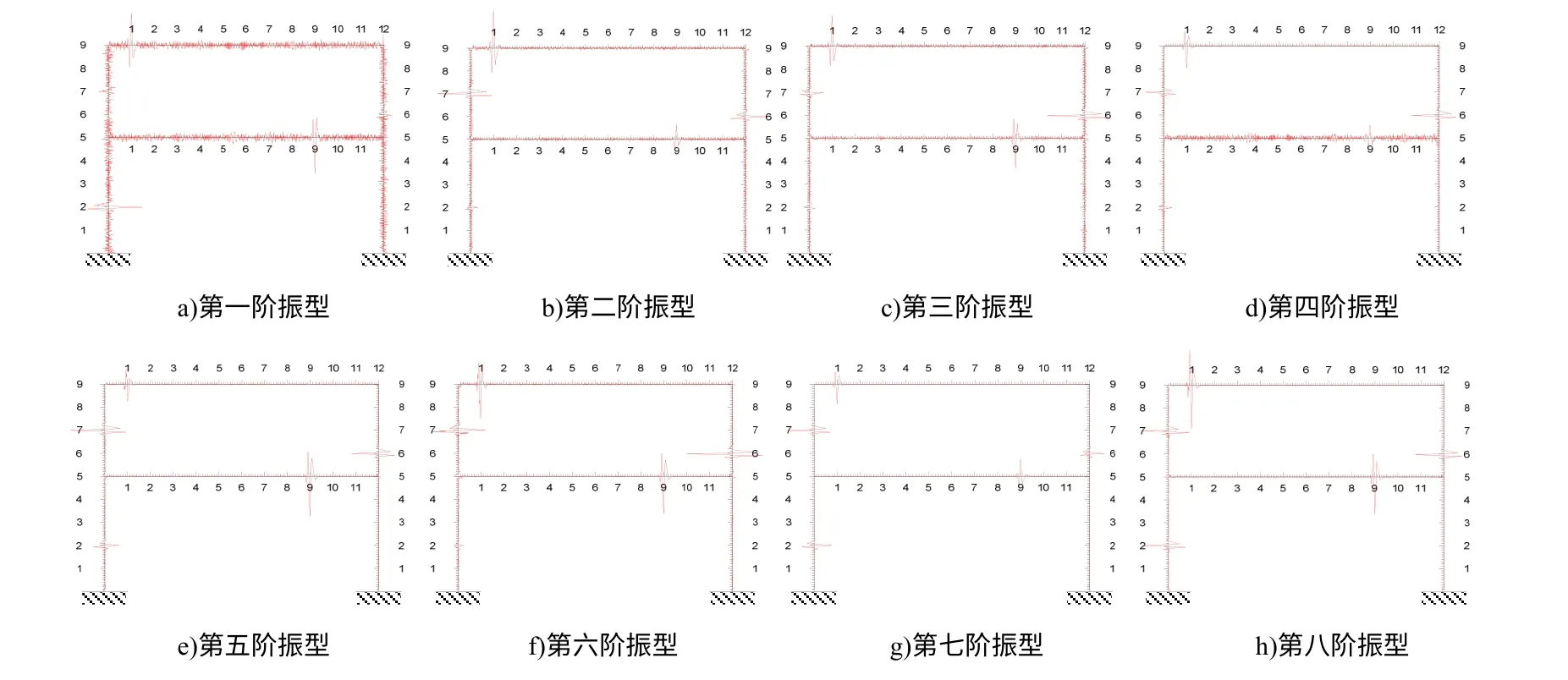
圖3 工況一下框架振型的小波變換結果

圖4 工況二下框架振型的小波變換結果

圖5 工況三下框架振型的小波變換結果

綜合3 種情況可知：框架結構發生損傷時，通過對振型的曲率模態進行小波變換，可以根據變換系數的模極大值來定位結構損傷的位置，但模極大值的大小與損傷程度的對應關系不確定﹒

4 結論

1)運用db3 小波對框架結構模態曲率進行15層連續小波分解，其小波分解系數模極大值準確指示了框架結構損傷的位置﹒

2)當損傷位置處于某階振型的平衡位置時，其小波變換系數對損傷位置的確定不明顯，通常為了增加損傷位置判斷的準確性，需要前面二、三階的振型數據﹒

3)結構損傷程度的確定是一個難題，不能根據小波變換系數模極大值來確定損傷程度﹒因此，進一步討論其它指標來確定結構損傷的程度是必要的﹒