基于多元回歸的高鐵墩臺沉降形變預測分析

許 韜，黃長軍, ，趙 鑫

(1. 湖南城市學院 市政與測繪工程學院，湖南 益陽 413000；2. 湖南城市學院規劃建筑設計研究院 湖南省城鄉生態規劃與修復工程技術研究中心/湖南省博士后流動站協作研發中心，湖南 益陽 413000； 3. 湖南有色金屬職業技術學院 建筑工程系，湖南 株洲 412000)

隨著經濟的快速發展，高鐵已經成為我國公共交通體系中非常重要的組成部分﹒高鐵高速的運行速度，對其設計和施工提出了更高的要求﹒橋梁作為高鐵線下工程重要的組成部分，由于受外界因素引發或自身結構的變形都可能存在安全隱患，成為發生災難性事件的誘因[1]，因此，對高鐵橋梁的變形監測則變得至關重要﹒墩臺作為橋梁重要的組成部分，其形變在量級上往往呈現出微小的特點﹒高鐵墩臺在形變監測過程中時常會受到外界條件或者隨機噪聲的干擾，使得采集到的數據以及后處理預測數據顯現出較大的波動，從而給數據分析和后續的變形預測帶來較大影響[2]﹒目前，一些預測方法例如灰色理論法，時間序列模型、回歸模型等預測模型法在高鐵形變預 測中得到應用，然而每種預測方法受其自身模型特點和外界條件的限制，具有一定的適用范圍﹒因此，在利用預測模型法時需結合實際工程情況，根據工程實際觀測條件，選擇合適的預測模型和方法[3]﹒考慮到回歸模型構建簡單的特點，本文以武廣鐵路線上位于韶關市湞江區梅村境內的梅村特大橋的30#墩臺為研究對象，引入多元回歸模型對高鐵墩臺變形數據分析處理，在顧及溫度和荷載對墩臺作用基礎上，利用Matlab 建立了多元回歸預測模型，與傳統的GM(1, 1)模型進行對比驗證，并對其預測精度進行分析和評價﹒

1 多元回歸法

回歸分析法是數理統計中最成熟、最常用的一種方法，在進行預測分析方面，其適用于單點分析情況﹒該方法基于對變形觀測數據和影響因子進行回歸分析以及逐步回歸計算分析，由此得到變形與影響因子的函數關系式[4-5]﹒回歸分析需要定性地分析變量之間的相關關系，當自變量與因變量存在某種關系時，建立的多元回歸模型才有實際預測的意義﹒回歸分析模型包括線性回歸模型、一元線性回歸模型和多元線性回歸模型等[4]﹒本文主要介紹多元線性回歸分析法﹒

1.1 多元線性回歸分析

多元線性回歸法是研究因變量與多個自變量之間的不確定關系的基本方法﹒該方法應用于橋梁的變形預測分析就是通過分析變形監測的變形量與環境影響因素之間的相關性來建立模型﹒在多元回歸模型中，大多數非線性回歸模型可以通過變量的變化轉化為線性回歸﹒

1.2 回歸模型檢驗

對回歸方程的顯著性(有效性)進行檢驗，在選擇顯著性水平α 后，可用公式(9)檢驗原假設，假若公式(9)成立，即認為在顯著性水平α 下，多元線性回歸方程中因變量y 與自變量 x1, x2, …,xm之間存在顯著線性關系，方程回歸效果顯著，反之回歸效果不顯著﹒

2 實例分析

2.1 工程概況

為了對本文方法進行分析，選擇梅村特大橋為研究對象﹒該橋全長2 579.49 m，橋梁為直線橋，連續梁橋墩為29#～32#墩，其中30#和31#墩跨既有京廣線，墩身結構為直坡圓端形實心墩，兩墩身的高度分別為14 和10 m；基礎采用鉆孔灌注樁，樁徑為1.5 m，最長的樁為43.7 m，最短的樁為13.5 m，按柱樁設計；30#和31#墩為上覆粉質黏土和硬塑的地質條件，地基承載力為190～220 kPa；30#和31#支墩基礎處理采用條形混凝土基礎，支墩采用C 型鋼塔架進行拼裝，墩基礎表面采用C15混凝土封底，墩臺施工完成后4 w用漿砌片石回填至墩臺面[8]﹒

2.2 數據來源

本文主要以橋梁的墩臺沉降變形進行分析，考慮到溫度和荷載對墩臺沉降的影響，選取30#墩臺沉降監測的18 期數據(觀測時間間隔為3 d，數據見表1)，建立多元線性回歸預測模型﹒文中以前13 期數據建立預測模型，最后5 期數據作為檢驗數據﹒為驗證本文方法的有效性，以上述數據建立GM(1, 1)模型與本文方法進行比較分析﹒

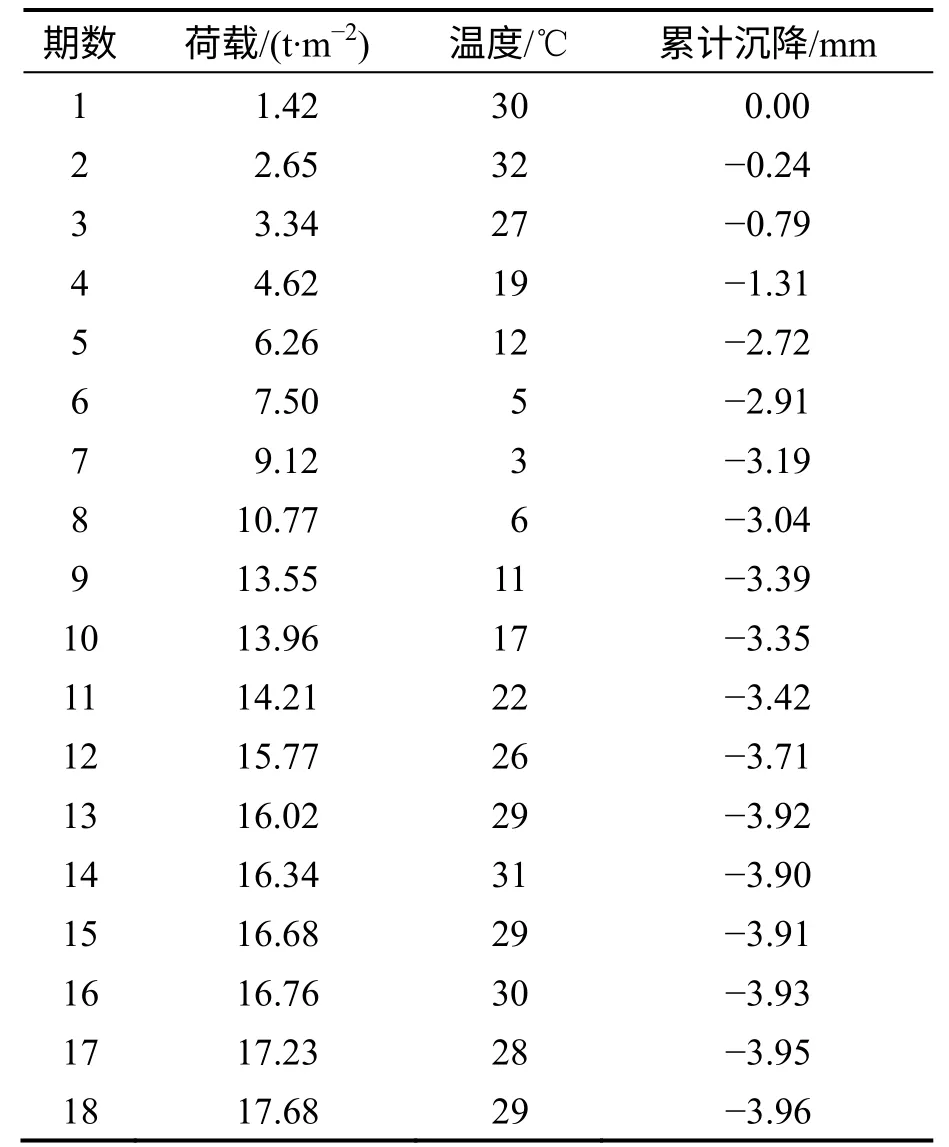
表1 30#墩臺沉降18 期觀測數據

2.3 模型建立

本文模型的建立利用Matlab 中的regress 函數進行數據處理和分析[9-10]，其形式如下：

式中，b 為回歸方程的參數估計值，b int表示b 的置信區間；stats 輸出結果中有3 個系數分別表示相關系數、F 統計量和估計誤差方差；y 為因變量；X 為自變量；alpha 為顯著性水平(一般取0.05)﹒

在本次橋梁墩臺沉降監測中主要考慮監測期內的荷載以及溫度對橋梁變形的影響，通過繪制出的荷載與累計沉降量的關系圖(見圖1)可以發現，荷載與沉降量具有一定的線性關系﹒令X1為荷載、X2為溫度作為自變量，Y 為累計沉降量，建立二元線性回歸模型﹒

圖1 荷載與累計沉降量關系

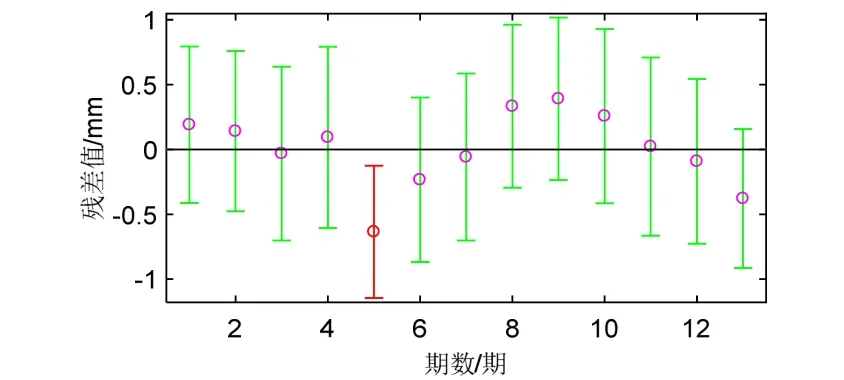
圖2 殘差分布

通過13 期觀測數據建立的殘差分布圖(見圖2)可看出，每個觀測值基本都處于其置信區間內， 但第5 個觀測值的置信區間未通過原點，該點可視為異常點，需要將該點進行去除后進行插值補充﹒本文采用拉格朗日插值法獲得第5 組數據的沉降量，計算插值結果為?2.47 mm﹒將插值獲得的數據進行回歸分析，利用rcoplot( r,rint)命令得到相應的殘差及其置信區間，見圖3﹒

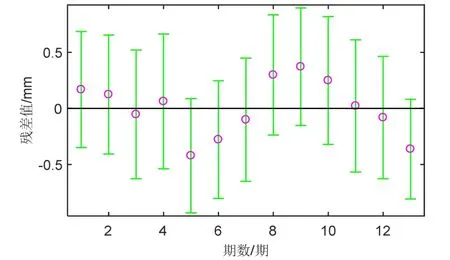
圖3 去除異常點后殘差分布

由圖3 可見相應的殘差都在其置信區間內，最大殘差為?0.422 mm，最小殘差為0.022 mm，殘差絕對值的均值為0.199 6 mm，殘差相對較小，由此說明模型的預測精度良好﹒最終獲得橋梁墩臺沉降實際值與回歸模型預測曲線，見圖4﹒

圖4 墩臺沉降實際值與回歸模型預測曲線對比

從圖4 可看出，回歸模型的預測值與實際值較接近，但第7 和第8 期數據稍微存在偏差﹒從這2 期的原始觀測數據來看，可能是由于受到外界其他因素(如暴雨等)影響而造成該點出現了上升的趨勢，從第9 期開始，該點又回歸到自然的形變狀態﹒從較差來看，最小較差僅為0.022 mm，最大較差為0.422 mm，沉降曲線基本與實際相似，說明回歸模型在整體上的預測是基本可靠的﹒

表2 回歸模型檢驗相關數值

表2 為計算得到的回歸模型檢驗結果，R 用 來衡量自變量x 與y 之間相關程度的大小﹒R 的值越接近于1，說明擬合得越好，結果表明自變量與因變量之間的關系為高度正相關，擬合優度較高﹒F 顯著性統計量為145.731 7，P 值(棄真概率)為4.02×10?8，遠小于顯著性水平0.05，說明該回歸方程回歸效果顯著﹒回歸標準差為0.243 9 較為接近0，說明模型預測值相對于實際沉降量的偏差較小，模型的預測精度較高﹒同時對于 X1的棄真概率為 3.44×10?8， X2的棄真概率為2.77×10?4，兩者都遠小于顯著性水平0.05，但 X1的棄真概率遠小于 X2的，說明荷載為影響墩臺沉降的主要因素，溫度對于墩臺沉降變形的影響相較于荷載來說是較小的﹒

2.4 精度分析與討論

為驗證本文方法的有效性，采用前13 期觀測數據，利用Matlab 編程建立GM(1, 1)預測模型，將GM(1, 1)模型計算的13 期預測值與回歸模型預測值進行比較，2 種預測模型前13 組數據預測曲線和殘差絕對值分別如圖5 和圖6 所示﹒

圖5 2 種預測模型前13 組數據預測曲線

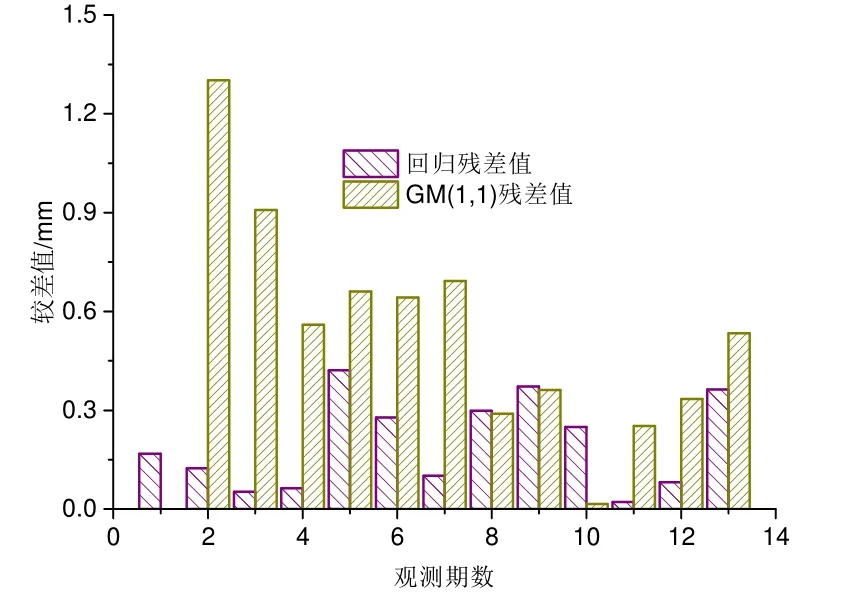
圖6 2 種模型殘差絕對值(前13 組)對比

從圖5 和圖6 可以看出，GM(1, 1)模型的殘差絕對值的均值為0.503 9 mm，而回歸模型的僅為0.199 6 mm，相較而言，回歸模型的殘差比GM(1, 1)模型的小，說明回歸模型的預測值更接近于實際沉降量，預測精度更高﹒

為再次驗證本文方法的可靠性，利用建立的模型，分別計算出最后5 期的沉降變形量，2 種模型對最后5 期的預測結果分別見圖7 和圖8﹒

圖7 2 種模型后5 組預測數據對比

綜上可知，在最后5 期的預測中GM(1, 1)模型的最大殘差達到了3.252 mm，最小殘差為1.004 mm；在回歸模型中最大殘差為?0.354 mm，最小 殘差為?0.022 mm﹒回歸模型的殘差絕對值都在0～0.4 mm 之間，殘差較小說明預測值與實測值很接近﹒通過以上數據計算可得GM(1, 1)模型最后5 組預測值的殘差均值絕對值為2.072 8 mm，回歸模型的最后5 組預測值的殘差均值絕對值為0.178 8 mm﹒通過對比2 組數據可看出回歸模型的預測精度要高于GM(1, 1)模型﹒回歸模型的預測曲線與實際沉降曲線更接近，而灰色模型的預測值與實際存在較大偏差﹒由此可見，在此工程案例中，回歸模型更適合預測墩臺沉降變形﹒

圖8 2 種模型殘差絕對值對比

3 結論

本文以梅村特大橋為研究對象，通過對橋墩墩臺的沉降監測，得到原始觀測數據﹒在對墩臺沉降進行多元回歸分析中，主要考慮了溫度和荷載對其的影響，然而，在實際的工程應用中，墩臺的形變會受到諸如水文地質、風力作用、土壤的物理性質以及濕度等多種因素的共同作用﹒為了得到更加精確的預測成果，需要從多方面考慮影響墩臺變形的因素，以便對橋梁整體變形進行準確的預測﹒根據原始觀測數據序列建立了基于墩臺沉降的二元線性回歸分析模型，由于在實際工程中橋墩的沉降會趨于穩定，而二元線性回歸模型中如果荷載一直增加則沉降預測值將會越來越大，這與實際情況相違背﹒因此，當橋墩沉降趨于穩定之后，二元線性回歸模型在后期的變化中不再適合用來進行沉降預測﹒

在本文分析的數據中，由前13 組數據建立模型，后5 組數據作為模型檢驗數據，當建立模型的數據選取不同時，模型精度也會有所改變，如減少原始樣本，回歸模型的精度可能會降低﹒此外，本文選取的二元線性回歸模型過于單一，為了提高預測精度，可以選擇多種方法結合的組合模型，如多元線性回歸+時序分析、多元線性回歸+BP 神經網絡模型以及多元線性回歸+趨勢分析等進行數據分析處理，以建立更加精確的變形預測模型，提高整體的預測精度﹒