數列常考綜合題型及破題思路探究

◇ 山東 杲 峰

數列是高中數學的重難點知識，一些綜合類的習題較為抽象，難度較大，是中學生最易失分的題型.

1 數列新定義題型及破題思路

數列新定義題在高中數學相關測試以及高考中出現頻率較高，對學生理解以及分析問題的能力要求較高.解題的關鍵在于深入理解新定義，充分挖掘隱含條件，靈活運用所學數列知識.為使學生掌握該類題的解題思路，實現迅速破題，教師在授課過程中應做好等差與等比數列知識的深入講解，不僅使其能準確地記憶相關的結論、性質，還應鼓勵其進行推導，知其然更知其所以然，避免死記硬背.同時，還要讓學生在解題過程中靈活運用題干已知條件，把握本質，實現數列各項關系的靈活推導與轉化.

例1已知正整數k，如數列｛an｝滿足以下等式：an-k+an-k-1+…+an-1+an+1+…+an+k-1+an+k=2kan，對所有的正整數n（n＞k）恒成立，則稱數列｛an｝為“P（k）數列”.（1）證明等差數列｛an｝為P（3）數列；（2）如數列｛an｝既是P（2）數列，又為P（3）數列，證明｛an｝是等差數列.

分析解答數列新定義綜合題的關鍵在于理解新定義，搞清楚題干中給出的等式關系.問題（1）只需要將k=3代入給出的等式，運用等差數列性質便不難證明.問題（2）難度稍大，應緊扣給出的條件，積極回顧所學的等差數列定義進行證明.

解析

（1）由已知條件可知，將k=3代入關系式易得：an-3+an-2+an-1+an+1+an+2+an+3=6an，由等差數列等差中項知識易得出等差數列｛an｝為P（3）數列.

（2）因為數列｛an｝既是P（2）數列，又為P（3）數列.

當n≥3時，an-2+an-1+an+1+an+2=4an， ①所以an-2+an-1=4an-（an+1+an+2），an+1+an+2=4an-（an-2+an-1）.

令n=n-1，則由式①可得

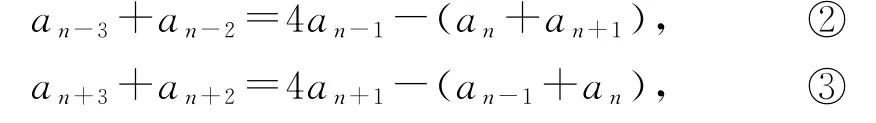
又因為當n≥4時，an-3+an-2+an-1+an+1+an+2+an+3=6an， ④

將②③代入④，得到an-1+an+1=2an（n≥4）.所以a3，a4，a5，…，an為等差數列.

設d 為其公差，在①中分別取n=4和n=3，化簡得到a2=a3-d，a1=a3-2d.

綜上，｛an｝是等差數列.

2 數列與方程題型及破題思路

學生對數列與方程綜合題型并不陌生.該類題難度一般不大，通常將數列的相關項或前n 項和與方程的兩根關聯起來.解答該類問題時需要求出方程的兩根，并根據已知條件確定數列的項或者數列的前n 項和.需要注意的是，如果是等比數列與方程相結合的題目，需要對求出的根進行合理取舍，準確求出數列通項公式后，再根據問題要求，靈活運用數列通項公式與前n 項和相關知識解答.

例2｛an｝是遞增的等差數列，且a2和a4為方程x2-5x+6=0的兩根.求數列的前n 項和Sn.

分析該題難度中等，根據給出的方程不難求出等差數列的通項公式.求數列的前n 項和可使用錯位相減法.

解析

因為a2和a4為 方 程x2-5x+6=0 的兩根，且數列為遞增數列，所以a2=2，a4=3.又因為a4-a2=2d，解得則所以

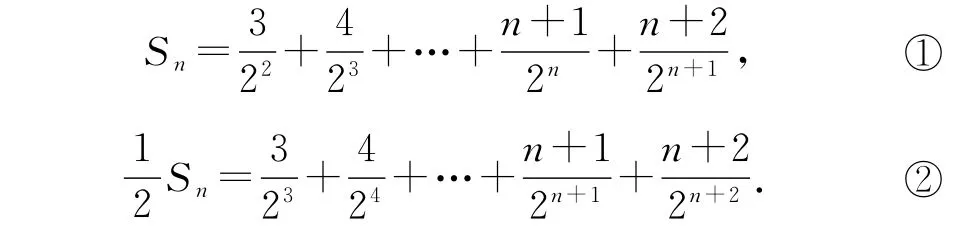
3 數列與函數題型及破題思路

數列是定義域為正整數的特殊函數，這就意味著一些函數知識可用于解答相關數列習題，包括函數圖象、函數性質、導數相關知識等，都能用于分析數列綜合題.為使學生更好地掌握該類題型的解題思路，應提高其函數知識應用意識，使其能靈活運用數列通項公式、前n 項和等知識解題.另外，在進行推理時應時刻關注數列的自變量n，保證得出的結論有意義，必要情況下可進行分類討論.

例3已知｛an｝為公差為d 的等差數列，點（an，bn）在函數f（x）=2x圖象上（n 為正數）.（1）證明數列｛bn｝為等比數列；（2）設a1=1，過函數f（x）圖象上點（a2，b2）的切線在x 軸上的截距為，求數列｝的前n 項和Sn.

分析（1）根據已知條件運用等比數列定義進行證明.（2）難度較大，需運用導數知識求得切線的斜率與在x 軸上的截距，得出數列｛an｝和｛bn｝的通項公式，而后使用錯位相減法求出Sn.

解析

（1）由 已知條 件 可知，bn=2an，則bn+1=2an+1，則bn+1／bn=2d，因此，｛bn｝是以2a1為首項，公比為2d的等比數列.

（2）對函數f（x）=2x求導得到f′（x）=2xln2，則過點（a2，b2）的切線方程為y-2a2=2a2ln2（xa2），令y=0，求得其在x 軸上的截距為

4 數列與不等式題型及破題思路

數列與不等式結合的綜合題難度較大，但授課中應注重樹立學生的自信，為學生歸納好該類題目的解題思路.該類題目通常和數列的前n 項和結合起來，因此，求解時可靈活應用數列前n 項和求解方法，包括公式法求和、分組求和、列項求和、錯位相減法求和等.而后使用基本不等式、函數單調性或放縮法等找到與要求解問題之間的聯系.尤其對學生而言，放縮法難度較大，可鼓勵學生記憶一些常見的放縮技巧，并不斷地訓練，直至正確牢固地掌握.

5 結語

為使學生掌握數列綜合題型的解題思路，教師在授課過程中應認真匯總常考的數列綜合題型，并為學生講解解題過程以及解題時應注意的關鍵點，使其積累豐富的解題經驗，以便遇到類似問題時能迅速破題.