子彈打木塊模型的解題方法
◇ 山東 李傳維
子彈打木塊問題是力學中的常見模型,綜合性較強,涉及運動學、牛頓運動定律、動量、能量等知識點.本文以兩道高考試題為例,試分析子彈打木塊問題的一般解法,希望對師生有一定的啟示.
1 實例分析
例1(2018年海南卷)如圖1,用長為l 的輕繩懸掛一質量為M 的沙箱,沙箱靜止.一質量為m 的彈丸以速度v 水平射入沙箱并留在其中,隨后與沙箱共同擺動一小角度.不計空氣阻力.對子彈射向沙箱到與其共同擺過一小角度的過程( ).
A.若保持m、v、l不變,M 變大,則系統損失的機械能變小
B.若保持M、v、l 不 變,m 變大,則系 統損失的機械能變小
C.若保持M、m、l不 變,v 變大,則系 統損失的機械能變大
D.若保持M、m、v 不變,l變大,則系統損失的機械能變大
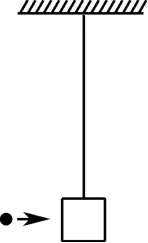
圖1
解析
子彈射向沙箱到留在其中的過程動量守恒,機械能減少.隨后子彈與沙箱共同擺動一小角度,此過程機械能守恒,沒有能量損失.碰撞過程,對于子彈和沙箱組成的系統,根據動量守恒定律可得mv=(m+M)v′.機械能減少量M)v2.聯立兩式可得變形為ΔEk=所以ΔEk與l無關,選項D 錯誤.若保持m、v、l不變,M 變大,可知ΔEk變大,所以選項A 錯誤.若保持M、v、l 不變,m 變大,可知ΔEk變大,所以選項B 錯誤.若保持M、m、l 不變,v 變 大,可 知ΔEk變大,所以選項C正確.
例2(2011年全國卷Ⅰ)裝甲車和戰艦采用多層鋼板比采用同樣質量的單層鋼板更能抵御穿甲彈的射擊.通過對以下簡化模型的計算可以粗略說明其原因.質量為2m、厚度為2d 的鋼板靜止在水平光滑桌面上.質量為m 的子彈以某一速度垂直射向該鋼板,剛好能將鋼板射穿.現把鋼板分成厚度均為d、質量均為m的相同兩塊,間隔一段距離水平放置,如圖2 所示.若子彈以相同的速度垂直射向第一塊鋼板,穿出后再射向第二塊鋼板,求子彈射入第二塊鋼板的深度.設子彈在鋼板中受到的阻力為恒力,且兩塊鋼板不會發生碰撞,不計重力影響.
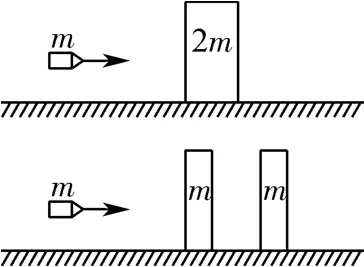
圖2
解析
設子彈以某一速度v0垂直射向質量為2m的鋼板,剛好能將該鋼板射穿,設射穿后鋼板和子彈速度相同為v,由動量守恒定律得mv0=3mv,動能損失為根據能量守恒定律得ΔEk=2Ffd.
鋼板拆分后,設穿過第一塊鋼板后子彈與鋼板的速度分別為v1、v1′,且v1大于v1′.則由動量守恒定律得mv0=mv1+mv1′.損失的動能ΔEk′=Ffd.ΔEk′=
設子彈射入第二塊鋼板后的共同速度為v2,根據動量守恒定律得mv1=2mv2.損失的動能ΔEk″=
設射入第二塊鋼板的厚度為x,根據能量守恒定律得ΔEk″=Ffx.
2 方法總結
通過上述兩道例題,總結子彈打木塊模型的一般解決方法如下:1)利用動量守恒定律、動量定理解決問題.在相關公式中,會涉及子彈、木塊的質量,碰撞前后的速度.如果涉及擊穿時間或者平均沖力、平均阻力,可以選用動量定理.2)利用功能關系、能量守恒定律解決問題.如果涉及能量問題,根據不同的情況,可以選用動能定理、功能關系及能量守恒定律,實現功能互求或不同形式的能量互求.能量公式中涉及的物理量有速度、動能、位移、相對位移、熱量等.3)利用牛頓運動定律、運動學公式解決問題.子彈打木塊模型中,涉及的運動一般可視為勻變速直線運動.4)子彈擊穿木塊后,子彈速度不小于木塊速度.
子彈打木塊模型是力學綜合類問題,只要從動量、能量、力與運動這三個方面入手分析,問題便可得以解決.

