加速度計貯存試驗及壽命評估方法研究
趙曉東,穆希輝
(1.陸軍工程大學石家莊校區 彈藥工程系,河北 石家莊 050003;2.32181部隊,河北 石家莊 050003)
0 引言
加速度計作為精確制導彈藥實現慣性制導的關重部件,具有長期貯存、一次使用的特點,因此準確評估其貯存壽命,對精確制導彈藥的可靠使用、維修決策和延壽處理都具有重要意義。
目前,主要通過加速試驗和自然貯存試驗兩種方式評估彈藥組件的貯存壽命。張煊工等[1]通過加速試驗,采用非線性維納過程和極大似然估計法,評估了末制導炮彈控制艙光耦的貯存壽命;王曉等[2]通過加速試驗,在威布爾分布假設下,建立了機電引信的貯存壽命預測模型,評估了機電引信的貯存壽命;胡明等[3]通過加速試驗建立加速模型,提出了適用于引信磁流變液解除保險機構貯存壽命的評估方法,并對其貯存壽命進行了評估;高永琪等[4]通過加速試驗,利用Hough變換法得到了加速壽命方程,最后外推得到了魚雷在常溫應力下的貯存壽命。上述研究都是通過加速試驗數據,采用一定方法建立產品的壽命模型,確定產品的貯存壽命。但由于加速試驗一般采用溫度應力作為試驗用力,而彈藥在實際貯存環境中所受應力更加復雜,因此只通過加速試驗評估部組件的貯存壽命存在一定局限性。
韓建立等[5]通過自然貯存試驗,采用殘差平方和最小原則方法,給出導彈貯存壽命的評估模型,預測了某型導彈的貯存壽命;陳佳欣等[6]依據3個不同地區的自然貯存數據,在威布爾分布假設下,通過極大似然估計法建立了彈藥貯存壽命評估模型,預測了不同地區的彈藥貯存壽命;王長安等[7]依據某型陀螺儀的定期檢測數據,建立了其貯存壽命評估模型,并依據該模型預測了陀螺儀的貯存壽命和開展加速試驗的加速因子;李湘寧[8]依據產品的短期自然貯存數據,在相似度控制、擬合分析的基礎上給出了產品的長期貯存壽命。上述研究都是依據彈藥導彈的部隊定期檢測數據來評估相關部組件的貯存壽命,但在實際中,受多種客觀因素影響,有些種類彈藥導彈的部隊定期檢測數據較為缺乏,使得無法單獨依據自然貯存試驗數據評估其貯存可靠性。
為解決某些彈藥導彈自然貯存數據缺乏問題、避免單獨依據加速試驗數據的局限性,本文提出一種結合自然貯存試驗數據與加速試驗壽命數據的產品貯存壽命評估方法。根據加速度計的物理失效機理,假設其可能服從的指數分布、威布爾分布、Ⅰ型極大值分布、Ⅱ型極大值分布4種壽命分布函數,依據其自然貯存試驗數據,采用極大似然估計法求得4種分布函數,并通過擬合優度檢驗來檢驗不同分布函數與數據的擬合度;設計并開展加速度計的步進加速試驗,得到其加速壽命數據,依據該數據估計得到威布爾分布和I型極大值分布的分布函數;通過加速因子變異系數法確定加速度計的壽命分布函數,并對比自然貯存中加速度計的失效率,驗證該方法的有效性。
1 自然貯存壽命評估
1.1 歷年檢測數據
為了鑒定貯存期不同階段加速度計的質量變化,需要在貯存過程中定期對加速度計進行檢測,檢測獲得的數據為成敗型數據。同時由于具體的失效時間未知,加速度計的檢測數據又是不完全數據。加速度計歷年的檢測數據如表1所示。
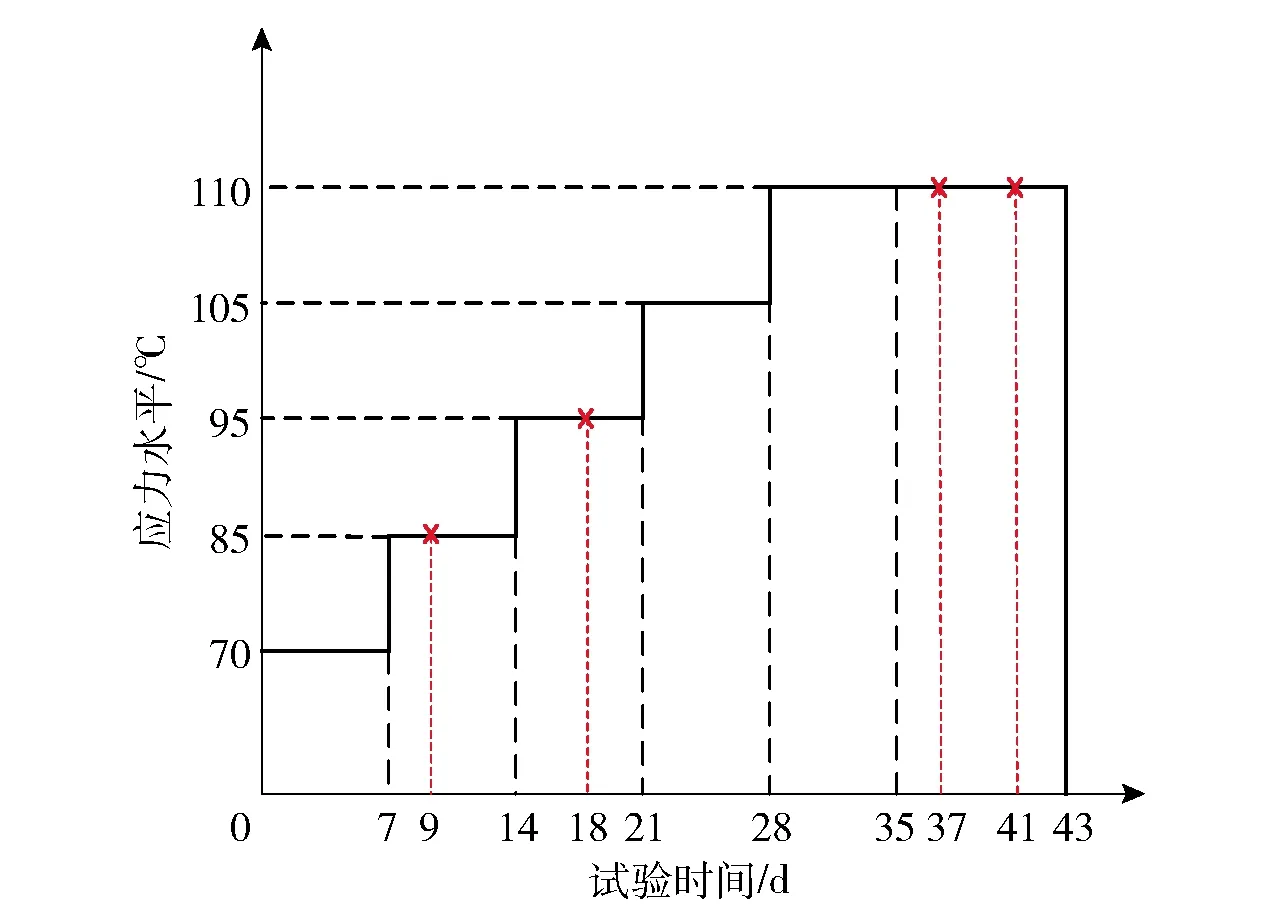
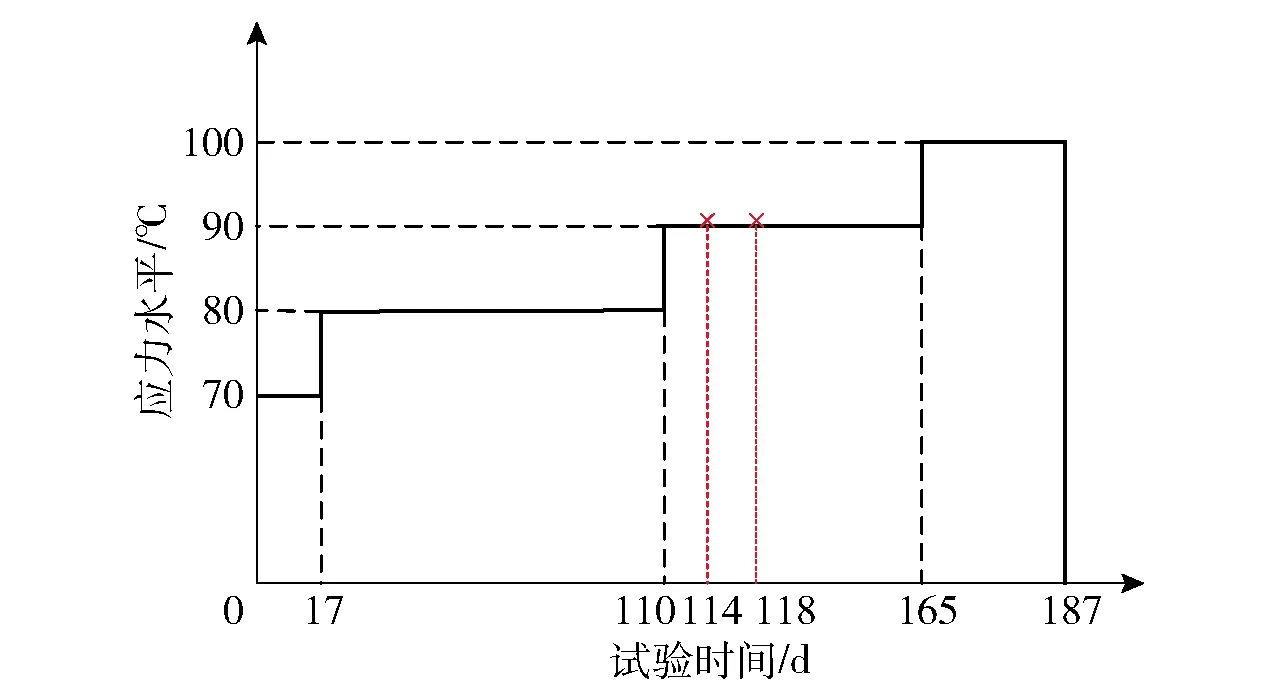
數據類型可以等效為:記t=(t1,…,ti,…,tk)為檢測時間點,k為自然貯存數據次序,在貯存了時間ti后,抽取ni件加速度計進行檢測,其中有Xi件失效,從而得到數據(ti,ni,Xi),式中:0 考慮加速度計的物理失效機理,假設其壽命分布的可能形式有指數分布、威布爾分布、Ⅰ型極大值分布以及Ⅱ型極大值分布,分布函數表達式如下: 表1 加速度計的歷年檢測數據Tab.1 Test data of accelerometer 式中:F(t)為壽命分布函數;θ為指數分布的率參數;m為威布爾分布和Ⅱ型極大值分布的形狀參數;η為威布爾分布和Ⅱ型極大值分布的尺度參數;μ為Ⅰ型極大值分布的位置參數;σ為Ⅰ型極大值分布的尺度參數。 χ2統計量的形式為 (1) (2) 為進一步明確檢驗的置信度,可計算檢驗的擬合優度p值,其計算公式如下: (3) 擬合優度可以衡量假定的分布與試驗數據的擬合程度,且擬合優度p值越大,表明擬合程度越好。 采用極小卡方估計法對加速度計的自然貯存壽命進行評估,其結果如表2所示。表2中:為指數分布率參數的估計值;為威布爾分布和Ⅱ型極大值分布尺度參數的估計值;為威布爾分布和Ⅱ型極大值分布形狀參數的估計值;為Ⅰ型極大值分布位置參數的估計值;為Ⅰ型極大值分布尺度參數的估計值;t0.95為可靠度為0.95的貯存壽命。 表2 加速度計自然貯存壽命評估結果Tab.2 Evaluated results of accelerometer natural storage life 從表2中可以看出,威布爾分布和Ⅰ型極大值分布的擬合優度p值更大,可靠壽命的估計值也更加符合實際,故可以初步確定加速度計的壽命分布函數為威布爾分布或Ⅰ型極大值分布。 依據彈藥洞庫的貯存規范(溫度小于30 ℃,濕度小于70% RH)推斷其在貯存過程中敏感應力主要包括溫度和濕度,因此選擇溫度、濕度為加速試驗的應力類型。但是,根據加速度計預試驗的分析結果發現,濕度應力并不是加速度計失效的關鍵應力,因此,正式加速試驗僅采用溫度應力作為加速應力。 由于確定溫度應力為加速應力,選擇Arrhenius模型[9-10]作為加速模型,其描述壽命特征與溫度的關系如下: L=AeEa/(kT), (4) 式中:L表示壽命特征;A為與溫度無關的未知常數;Ea為激活能(eV),表示分子參與反應所需的能量;k為玻爾茲曼常數(8.623×10-5eV/K);T為溫度(K)。 設步進應力加速壽命試驗共有d個應力,S0 2.2.1 威布爾分布 假設各應力水平下加速度計貯存壽命服從威布爾分布,則分布函數為 Fi(t)=1-exp [-(t/ηi)mi], (5) 式中:mi和ηi分別為應力Si下的形狀參數和尺度參數。 為求解威布爾分布下加速度計壽命分布模型參數,現做以下基本假設: 假設1各應力水平Si下的形狀參數mi相等,即m0=m1=…=mn=m. 假設2產品的特征壽命ηi與所施加應力Si滿足Arrhenius加速方程: lnηi=a+bφ(Si), (6) 式中:a=lnA;b為未知參數,b=Ea/k;φ(Si)=1/Si=1/Ti. 假設3產品剩余壽命僅依賴于失效累積量和當時的應力水平,與累積方式無關(Nelson累積失效假定)[11-13]。 由假定Ⅰ分布的形狀參數mi相等,應力水平Si下第j個失效樣本的失效時間折算到給定應力Sq(q=0,1,2,…,d)下的失效時間為 (7) 式中:Ki,q為應力水平Si與Sq之間的加速因子,Sq為從所有的應力水平中選定的一個應力水平, (8) ηq為應力水平Sq下的特征壽命,ηi為應力水平Si下的特征壽命,Tq為應力水平Sq下的溫度,Ti為應力水平Si下的特征壽命;tij為應力水平Si下第j個失效樣本在Si下的試驗時間;l為應力水平Si與Sq之間的其他應力水平數;τl為樣本在應力水平Sl下的試驗時間。 到達試驗截尾時間τk仍未失效的樣本,折算到給定應力水平Sq下的時間為 (9) 根據以上分析,可得似然函數如下: (10) 式中:f(tij,q)為應力水平Si下第j個失效樣本在給定應力Sq下的分布函數;F(τq)為試驗截止仍未失效樣本在給定應力Sq下的分布函數。 對數似然函數如下: (11) 通過解如下方程組: (12) 加速度計在常規應力水平下特征壽命η0的估計值為 (13) 式中:T0為常規應力水平下的溫度。 在給定可靠度R下,加速度計在常規應力水平下可靠壽命t0,R的估計值為 0,R=(-lnR)0= (14) 2.2.2 Ⅰ型極大值分布 假設各應力水平下加速度計壽命服從Ⅰ型極大值分布,則分布函數為 (15) 式中:μi和σi分別為應力水平Si下的位置參數和尺度參數。 為求解Ⅰ型極大值分布下加速度計壽命分布模型參數,現做以下基本假設[14-15]: 假設4各應力水平Si下的尺度參數σi相等,即σ0=σ1=…=σn=σ. 假設5產品的特征壽命exp (μi)與所施加應力Si滿足Arrhenius加速方程: exp (μi)=a+bφ(Si), (16) 式中:φ(Si)=1/Si=1/Ti. 假設6產品剩余壽命僅依賴于失效累積量和當時的應力水平,與累積方式無關(Nelson累積失效假定)。 由假定Ⅰ型極大值分布的尺度參數σi相等,應力水平Si下第j個失效樣本的失效時間折算到給定應力水平Sq下的失效時間為 (17) 到達試驗截尾時間仍未失效的樣本折算到給定應力水平Sq下的時間為 (18) 式中: (19) exp (μq)為應力水平Sq下的特征壽命,exp (μi)為應力水平Si下的特征壽命。 似然函數如下: (20) 對數似然函數如下: (21) 通過解如下方程組: (22) 加速度計在常規應力水平下特征壽命exp (μ0)的估計值為 exp (0)=exp (q)exp (23) 在給定可靠度R下,加速度計在常規應力水平下可靠壽命t0,R的估計值為 0,R=exp {-ln[-ln (1-R)]+0}= (24) 在步進應力加速試驗中,加速因子常用于不同應力水平之間失效信息的轉換以及加速應力到常規應力的外推,因此加速因子的穩定性對于試驗結果分析的精度起著至關重要的作用[16]。由于試驗樣本之間存在隨機性,且測量和評估過程中不可避免地引入隨機誤差,在不同壽命分布模型假設下往往得到不同的加速因子。本文基于加速因子變異系數的模型選擇方法,通過比較不同壽命分布模型假設下得到的加速因子變異系數(標準差與均值的比值),對壽命分布模型進行選擇。 在加速貯存試驗中,由于任意兩個應力水平之間均存在加速因子,加速因子變異系數的定義并不唯一。本文選用高應力與常規應力間的加速因子變異系數,其通常作為加速試驗中由高應力外推正常應力下的可靠性指標,形式如下: (25) 式中:CV(K0,q)為高應力與常規應力間的加速因子變異系數,K0,q為高應力與常規應力間的加速因子;σ(K0,q)為K0,q的標準差估計;μ(K0,q)為K0,q的均值估計。 對于威布爾分布, (26) 其均值的估計為 (27) 標準差的估計為 (28) (29) (30) Lwei表示威布爾分布下的似然函數,E表示數學期望。 故威布爾分布下加速因子的變異系數為 (31) 式中:σwei(K0,q)為威布爾分布下K0,q的標準差估計;μwei(K0,q)為威布爾分布下K0,q的均值估計;0,q為高應力與常規應力間的加速因子估計。 對于Ⅰ型極大值分布,同理可得其加速因子的變異系數為 (32) 式中:σext(K0,q)為Ⅰ型極大值分布下K0,q的標準差估計;μext(K0,q)為Ⅰ型極大值分布下K0,q的均值估計;0,q為高應力與常規應力間的加速因子估計, (33) (34) (35) 得到威布爾分布和和Ⅰ型極大值分布加速因子的變異系數后,比較兩種不同分布的加速因子變異系數大小,選擇加速因子變異系數小的分布作為加速度計的壽命模型。 在加速度計加速貯存壽命試驗設計之前,需開展加速預試驗作為加速貯存壽命摸底試驗,得到的試驗信息主要包括以下3點: 1)確認加速度計的可加速性; 2)確定加速度計加速退化應力水平上界; 3)確定加速度計性能參數是否存在退化規律。 根據加速度計的貯存規范,選擇溫度和濕度作為預試驗的應力類型。預試驗共開啟2個溫度、濕度試驗箱進行試驗,一個為溫度單應力試驗,一個為恒濕(75%RH)溫度雙應力步進應力試驗。試驗過程中的試驗箱運用說明如下: A試驗箱進行高溫步進應力加速試驗,溫度應力依次為S1=70 ℃,S2=85 ℃,S3=95 ℃,S4=105 ℃,S5=110 ℃; B試驗箱進行恒濕(75%RH)溫度步進應力加速試驗,溫度應力依次為S1=70 ℃,S2=85 ℃,S3=95 ℃,S4=105 ℃,S5=110 ℃. 當B試驗箱溫度應力高于95 ℃時無法施加濕度條件,直接將B試驗箱中的樣本拿到A試驗箱,一并進行試驗。 用5個同批次的加速計新品作為試驗樣品,進行35 d不間斷試驗。另外根據人機功效最大化原則,在溫度應力S1、S2、S3、S4下各試驗、測試7 d,如果還有樣品沒有失效,則繼續放在S5下進行試驗;每一應力水平下試驗時間包括應力持續時間、加速度計檢測時間以及升溫降溫時間。 通過專用的檢測設備,采用定周期檢測方法進行加速度計失效時間的測量,每周檢測3次,分別在每周的第2 d、第5 d和第7 d(即改變應力水平時)開始檢測程序:進行檢測時,需將加速度計恢復在正常應力水平S0(室溫25 ℃)下進行檢測,以保證測試條件的一致性。 依據上述試驗方案,取5個樣本開展預試驗,其應力設置與樣本失效分布如圖1所示。 圖1 加速度計預試驗失效分布圖Fig.1 Distribution map of accelerometer pre-test failures 4個失效樣本的失效模式依次為參數為0、零偏實測值與初始值相差大于3 Hz、標度因素K1超差、零偏值K0超差。4次失效分別發生在85 ℃(1個)、95 ℃(1個)以及110 ℃(2個)下,對失效樣本進行了失效分析。結果顯示,預試驗中2個失效樣本輸出異常;另外2個樣本超差。自然貯存失效的產品,由于管理原因,全部樣本由于過電壓應力而擊穿電容。根據預試驗結果,可得出以下結論: 1)濕度應力對加速度計的影響不大,故正式加速試驗將不考慮濕度應力; 2)加速度計具有顯著的可加速性; 3)110 ℃溫度應力下使加速度計損壞,即找到了破壞極限,因此正式加速試驗的最高應力水平為100 ℃,當然也可取105 ℃. 取7個樣本開展加速貯存壽命正式試驗,通過對加速度計的預試驗結果進行分析,設置高溫步進應力加速壽命試驗的最低應力水平為70 ℃,最高應力水平為100 ℃(稍低于預試驗摸底的極限最高溫度應力110 ℃)。設定4個溫度應力水平,根據溫度應力倒數等間隔取值公式,應力水平設置如下:S1=70 ℃、S2=80 ℃、S3=90 ℃、S4=100 ℃. 采用定周期檢測方法,從試驗開始,每隔2 d開始檢驗程序。進行檢測時,停止并打開試驗箱,將部組件溫度自然冷卻到正常應力水平(室溫25 ℃),以保證測試條件的一致性。檢測時間控制在2 h之內,檢測完畢后對性能數據進行分析,明確失效樣本個數,以確定是否改變應力水平。 綜合考慮時間、成本和試驗數據精度確定各試驗應力水平下的試驗時間。若低溫度應力試驗時間過長,則會增加試驗時間、提高試驗成本;若過早進入高溫度應力水平試驗,則由于采用定周期的檢測方式,會加大測量數據的誤差。因此,結合預試驗結果,正式試驗時在80 ℃和90 ℃下的試驗時間較長,在70 ℃和100 ℃下的試驗時間較短,在試驗開展187 d后,終止加速貯存試驗。 加速度計正式加速試驗應力設置與樣本失效分布如圖2所示。 圖2 加速度計加速試驗失效分布圖Fig.2 Distribution map of accelerometer accelerated test failures 結合預試驗和加速試驗失效數據,將加速度計失效時間折算到90 ℃. 在威布爾分布假設下,可以得到模型未知參數的極大似然估計值如下:m=1.841 2,η90 ℃=6.338月,b=7 979.73. 對數似然函數值為lnL=-19.445 0. 據此,可得加速模型如下:lnηi=-20.127 1+7 979.73/Ti. 在Ⅰ型極大值分布假設下,可以得到模型未知參數極大似然估計值如下:σ=1.5,μ90 ℃=0.731,b=9 507.283. 對數似然函數值為lnL=-18.239 0. 據此,可得加速模型如下:μi=-25.449 0+9 507.283/Ti. 根據基于加速因子變異系數的模型選擇方法,分別計算威布爾分布假設和Ⅰ型極大值分布假設下90 ℃與25 ℃之間加速因子的變異系數,具體如下: 威布爾分布假設下, Ⅰ型極大值分布假設下, 由于CVwei(K0,q)>CVext(K0,q),故選擇Ⅰ型極大值分布作為加速度計的貯存壽命分布函數。 利用常規應力下加速度計的失效分布函數,預測不同貯存年份加速度計的可靠度,并與標準貯存環境中檢測數據確定的加速度計可靠度進行對比。結果如表3所示。 表3 標準貯存環境中加速度計故障統計表Tab.3 Accelerometer failures statistics in standard storage environment 同理可得其他貯存年份可靠度的相對誤差,結果如表4所示。 表4 不同年份加速度計可靠度預測值與估計值對比Tab.4 Comparison of predicted and estimated values of accelerometer reliability 從表4中可以看出,各年份的相對誤差都很小,從而驗證了加速度計失效分布函數的準確性。 本文提出一種綜合利用加速試驗與自然貯存試驗的加速度計貯存壽命評估方法,通過自然貯存壽命評估,設計并開展加速試驗和加速貯存壽命評估,確定Ⅰ型極大值分布為加速度計的貯存壽命分布函數,得到其在常規應力水平下,可靠度為0.90的可靠壽命為14.917 6 a,可靠度為0.95的可靠壽命為10.052 4 a. 通過與常規應力下標準貯存環境中加速度計可靠度的對比,驗證了該方法的有效性,表明該方法是可以工程推廣的。1.2 分布函數模型


1.3 極小卡方估計法


1.4 擬合優度檢驗
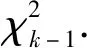

1.5 評估結果

2 加速壽命試驗模型確定
2.1 加速模型
2.2 壽命模型
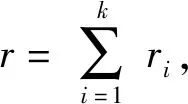
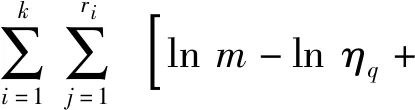
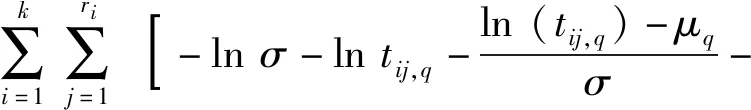
3 基于加速因子變異系數的模型選擇方法
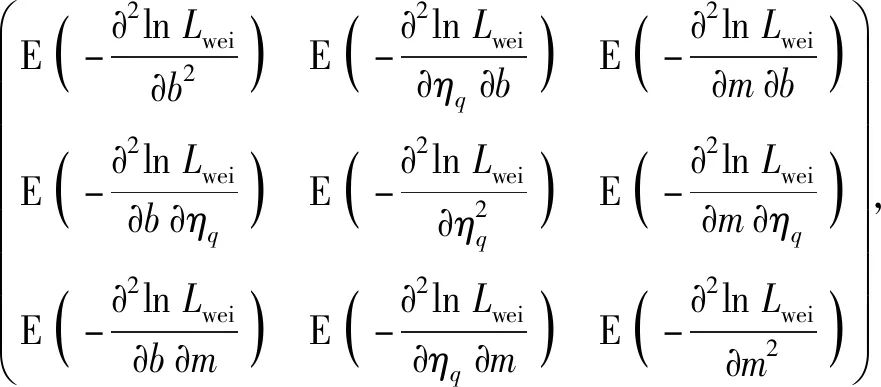
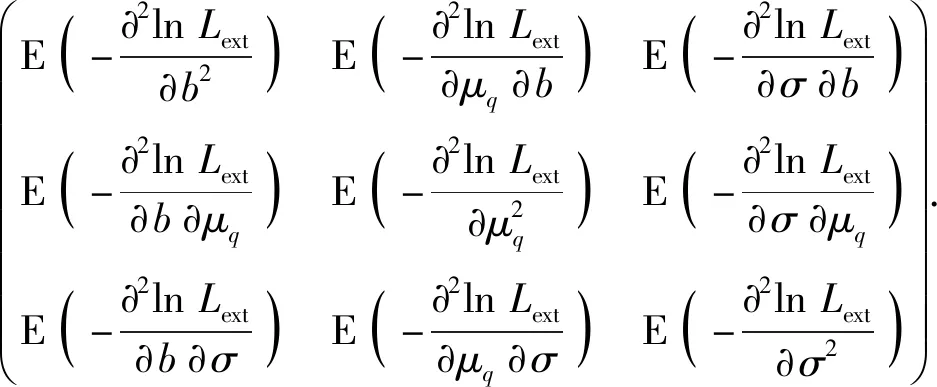
4 加速貯存壽命試驗
4.1 預試驗
4.2 正式加速試驗
5 加速貯存壽命評估
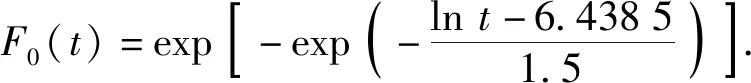


6 結論

