高揮發性液體傳質速率機理和實驗研究

劉文杰，白春華，劉慶明，姚箭，王曄

(1.北京理工大學 機電學院，北京 100081; 2.華北科技學院 研究生部，河北 廊坊 065201)

0 引言

云爆武器與常規武器不同，其在大空間范圍內形成可燃云霧，起爆后發生體積爆轟，具有超壓衰減速度慢、作用時間長、能夠產生窒息效應等特點[1]。云爆武器對隱蔽目標和軟目標的毀傷效果好[2]，能夠在較大范圍內對人員造成傷害，使其死亡或失去戰斗能力[3]。新一代二次引爆性云爆武器生產過程中用到大量乙醚，其易燃性和強揮發性決定了在生產、運輸、貯存、使用過程中有著較大的危險性。

國內外學者對可燃云霧形成影響因素及影響規律進行了研究[4-6]。云爆劑在分散拋灑過程中受到裝藥和彈體結構的影響。在可燃蒸氣云的形成方面，對其分布特性、固體與液體分布狀態和霧滴氣體液體(簡稱氣液)傳質過程進行了研究[7-8]。液體的氣化速度對蒸氣云形成起決定性作用，液體的快速氣化增加了可燃蒸氣云形成的可能性，增大了事故發生的可能性。為保證云爆武器安全生產，非常有必要開展高揮發性液體揮發速率影響因素和影響規律的研究。

國內外學者對不同情況下的氣液傳質進行了研究[9-10]，其中針對高揮發性液體的研究較少，各影響因素對氣液傳質速率的影響規律研究不足，不同物理屬性液體研究不系統。本文以乙醚為對象對高揮發性液體揮發速率進行實驗研究，分析液體溫度、液體表面氣體流速對揮發速率的影響。以Treybal[11]氣液傳質理論為依據，結合馮·卡門相似原理和格拉罕姆擴散定律，根據Mackay[12]和Sutton[13]提供的參數值，對氣液傳質計算公式進行推導。以實驗數據為依據，根據麥克斯韋熱運動速率分布律計算理論對實驗結果進行分析，總結得到新的氣液傳質速率計算方法。通過對比液柱下流質量損失率的實驗結果與計算結果，對計算方法的準確性進行驗證。

1 氣液傳質實驗

建立風道，進行氣液傳質速率實驗研究，實驗系統如圖1所示。使用有機玻璃創建長方體實驗作用區域，尺寸為0.2 m×0.2 m×1.0 m. 在實驗區域中間下部放置圓柱形液體盛料桶，直徑10.39 cm，高11.02 cm，盛料桶上邊緣高出長方體管道下表面0.5 cm，實驗時液體表面距離盛料桶上邊緣0.3 cm. 風機、進氣管道和壓力平衡膜為矩形管道提供一定風速穩定的空氣流。風機使用管道風機，口徑尺寸為0.2 m，最大氣體流量為1 205 m3/h. 進氣管道長0.15 m、直徑0.2 m，管道末端的10 mm厚腔體為壓力平衡膜作用提供空間，壓力平衡膜使用美國明尼蘇達礦業及機器制造公司生產的空氣過濾網。

圖1 液體質量揮發實驗系統圖Fig.1 Liquid mass volatilization experiment system

實驗系統共安裝3種傳感器，管道頂板安裝有溫度傳感器和風速傳感器，其安裝位置距離風道兩側0.1 m，距離進風端分別為0.47 m和0.53 m. 溫度傳感器量程范圍為-30～50 ℃，測量精度為0.1 ℃，溫度探頭位于液面下方1 cm處，如圖1(a)所示。風速傳感器量程為0～5 m/s，測量精度為0.02 m/s，傳感器探頭位于液面上方1 cm處，如圖1(a)所示。質量傳感器為懸臂梁單點式稱重傳感器，放置在盛料桶下，如圖1(b)所示，量程為1 500 g，測量精度為0.1 g. 根據風速傳感器測量的數據調節風機氣流量，保證液面上方空氣流速在目標風速±0.02 m/s范圍內。

使用濃度為99.5%的乙醚作為實驗對象，其部分物理屬性在表1中列出。

表1 乙醚物理屬性[14]Tab.1 Physical property of diethyl ether[14]

在風道內制造風速為0.5 m/s、1.0 m/s、1.5 m/s、2.0 m/s和2.5 m/s的空氣流，對乙醚在不同風速條件下的揮發速率進行實驗，單次需要乙醚909.9 mL，記錄液面上方10 mm處風速、液面下10 mm處溫度和質量，每次實驗持續時間為600 s.

2 實驗結果與分析

2.1 液體揮發預測模型

根據不同液體表面溫度及液面上層空氣流動速度計算氣液傳質速率，采用Mackay等[12]1973年提出的氣液傳質速率計算公式，計算低層大氣液體的揮發速率：

(1)

式中：Q為氣液傳質速率(kg/(s·m2))；K為傳質項(m/s) ；Mw為液體摩爾質量(kg/kmol)；A為液體表面面積(m2)；pv為飽和蒸氣壓力(Pa)；T為液體溫度(K)；R為理想氣體常數，R=8 314 J/(kmol·K)。

從(1)式中可以看出，液體質量揮發速率與溫度呈反比，與分子動力學的分析結果相反。根據熱運動麥克斯韋速率分布律可知，分子熱運動速率與溫度的平方根呈正比，液體分子為了克服分子間的相互作用需做功，動能轉換為勢能，動能越大、液體分子越容易擴散到空氣中，揮發速率與滿足條件——動能大于等于勢能的分子數量呈正比，分子的熱運動動能與分子熱運動速率的平方呈正比，因此推導得到揮發速率與溫度呈正比。

本文對溫度與揮發速率的關系進行修正，根據上文得到的結論，Q與溫度呈正比關系，因此在Mackay等[12]提出的氣液傳質速率計算公式后增加溫度系數：

(2)

式中：θT為溫度修正項；Tb為液體沸點溫度(K)；κ為溫度修正項系數。Sutton[13]使用馮·卡門相似原理及其參數文件推導，得到傳質項K的計算公式如下：

K=Cμαχβ，

(3)

式中：C為傳質系數(m/s)；μ為液面上方氣液相對速度；χ為液池直徑；α、β為相關系數。Dalton[15]給出的α取值為1，1973年Mackay等[12]將α值優化為0.78. Sutton[13]確定β值為-0.11.

系數C與物質的施密特數SC相關，Mackay等[12]給出關系式為

C=4.82SC-0.67.

(4)

施密特數SC為運動黏性系數ν和擴散系數DM的比值，計算公式為

(5)

應用格拉罕姆擴散定律計算物質的空氣分子擴散系數DM(m2/s)，計算方法為

(6)

式中：DH2O為水的分子擴散系數(m2/s)；MH2O為水的摩爾質量(kg/kmol)。

根據(3)式～(6)式，得到K的計算方法如下：

(7)

結合(1)式～(7)式，得到揮發速率計算公式為

(8)

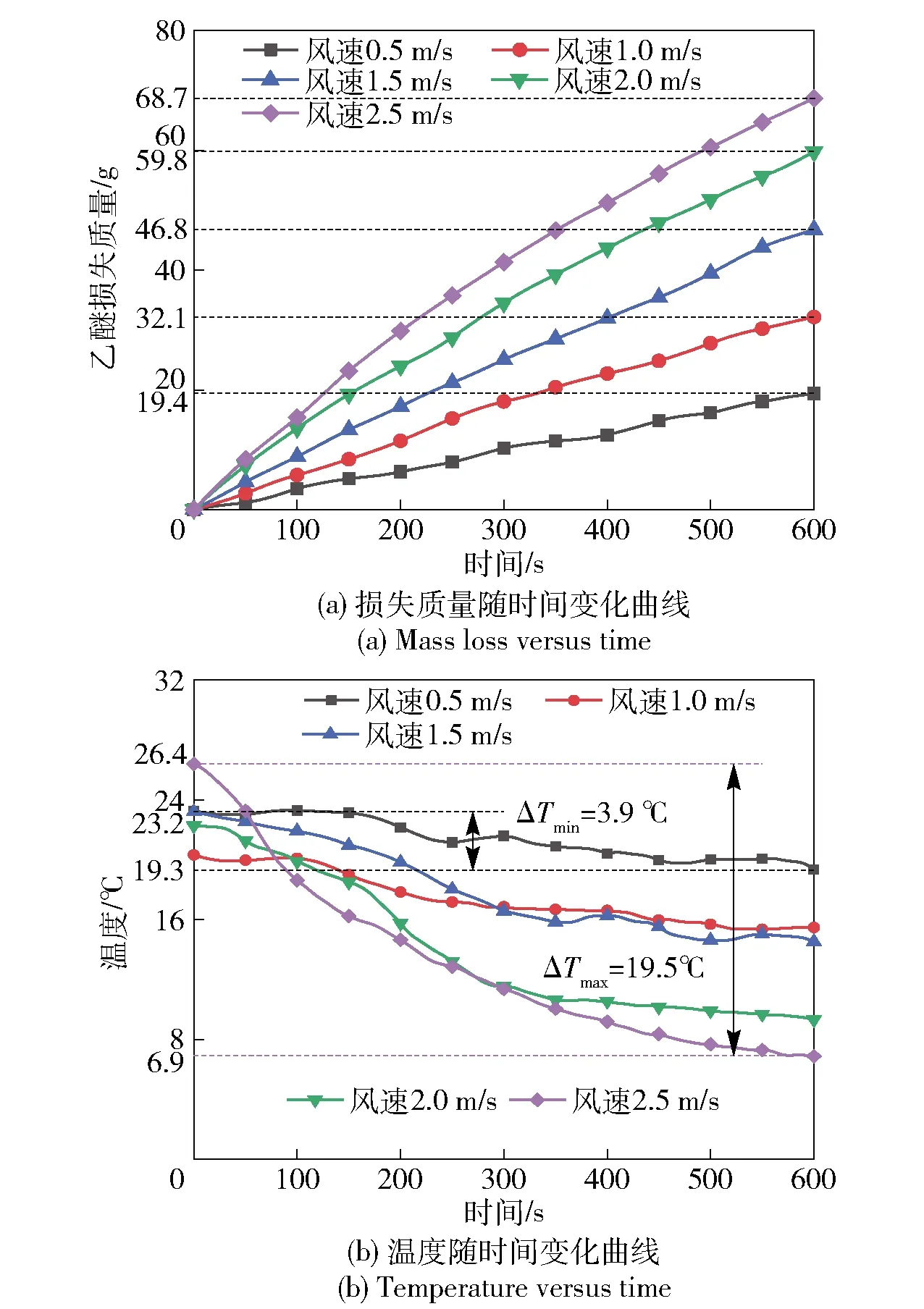
圖2 不同風速條件下風道內乙醚損失質量及溫度Fig.2 Mass loss and temperature of ether in air ducts at different wind speeds

2.2 結果規律分析

實驗得到損失質量及溫度隨時間的變化曲線分別如圖2(a)和圖2(b)所示。從圖2(a)中可以看出，風速越高、質量損失越嚴重，在忽略溫度影響的情況下，風速由0.5 m/s增大到2.5 m/s時質量損失由19.4 g增大到68.7 g. 從圖2(b)中可以看出，隨著時間的推進，乙醚溫度降低，實驗600 s內溫差最大的是風速為2.5 m/s時，溫差最大值ΔTmax=19.5 ℃，在0.5 m/s風速實驗條件下溫差最小，溫差最小值ΔTmin=3.9 ℃. 對比圖2(a)和圖2(b)可知，質量損失越大，對應溫度差越大，但呈非線性關系。

根據比熱容和揮發焓分別計算揮發吸收的總熱量和液體溫度降低釋放的總熱量，結果如表2所示。從表2中可以看出，隨著風速的增加，揮發吸收熱量和液體溫度降低釋放熱量均增加，但同一組實驗中揮發吸收的熱量與液體溫度降低釋放的熱量不同，揮發吸收的熱量均遠大于液體溫度降低釋放的熱量。造成這一現象的原因是容器內液體溫度分布不均勻，液體表面溫度與液體內部溫度差距很大，根據液面溫度進行計算，導致液體溫度降低釋放的熱量很大。

表2 不同風速條件下600 s時揮發吸收熱量和液體溫度降低釋放熱量Tab.2 Absorbing and releasing amounts of heat in 600 s at different wind speeds

圖3中給出了揮發速率隨時間變化的曲線。從圖3中可以看出：風速大于1.5 m/s時揮發速率隨時間呈明顯的下降趨勢；風速為1.5 m/s時，揮發速率隨時間同樣呈下降趨勢但并不明顯；風速小于1.5 m/s時，揮發速率隨時間沒有明顯變化趨勢，揮發速率基本處于恒定數值。對比相同風速條件下相同時刻的液面溫度，風速為2.5 m/s時，實驗前后溫度變化最大，對應揮發速率實驗前后揮發速率差距也最大，在0 s時刻揮發速率為0.077 g/s，在600 s時刻揮發速率為0.177 g/s，揮發速率差Δ達到0.100 g/s，這一過程中溫差為19.52 ℃；風速為0.5 m/s時揮發速率隨時間下降程度較弱，對應溫差僅有3.9 ℃. 因此，溫度對揮發速率是有影響的。

圖3 不同風速條件下揮發速率隨時間變化曲線Fig.3 Evaporation rate versus time at different wind speeds

2.3 溫度修正項系數

根據實驗數據確定溫度修正項系數κ. 根據對應時刻的液面下10 mm處溫度及液面上方10 mm處風速，取κ=1. 根據(8)式進行計算，得到計算值并與對應實驗值進行比較，取不同條件下比值的平均值，平均值為0.509，中位數為0.492，方差為0.076.

圖4為溫度修正項系數隨時間變化曲線圖。從圖4中可以看出：雖然溫度修正項系數波動較大，但在風速小于等于1.0 m/s時，溫度修正項系數在平均值附近波動；當風速大于1.0 m/s時溫度修正項系數隨時間呈總體下降趨勢，且風速越大、下降趨勢越明顯；當風速為2.5 m/s時，實驗首末系數差值最大達到0.50. 這是因為實驗測試過程中所測量溫度為液面下方10 mm處溫度，液面揮發吸熱使液面溫度下降，揮發速率越快吸熱越多，液面溫度越低。受液體傳熱速率的限制，液面下方10 mm處溫度比液面溫度低，且隨著時間的推進，溫度差越來越大。在同一時刻揮發速率越快，溫度差越大。使用液面下方10 mm處溫度進行計算時導致溫度修正項系數隨時間的推移呈總體下降趨勢。

圖4 溫度修正項系數隨時間變化曲線Fig.4 Temperature correction coefficient versus time

通過Meng等[16]給出的0.1 MPa壓力條件下乙醚密度ρ與溫度T的關系：

ρ=1 103.00-2.143 93T+4.947 97×10-3T2-7.368 06×10-6T-6

(9)

控制乙醚液體密度,使用實驗所得每秒液體質量損失量和液體初始溫度，利用流體仿真軟件Fluent二次開發技術[17-18]，對液體溫度場進行數值模擬，建立二維幾何模型計算600 s內液面下方1 mm處與10 mm處溫度差。計算結果如圖5所示。

從圖5中可以看出：在500 s時間內，隨著時間的推移溫度差越來越大，這一結果能夠解釋當風速較大時，隨著時間的推移溫度修正項系數不斷減小這一現象；但風速為2.5 m/s時，時間大于500 s時間段溫度差減小，這一現象是由于液體溫度差大，密度差大，液體內部流動加快，上層低溫液體向下層轉移增快，導致溫度差減小，但不影響其總體趨勢。

圖5 液面下方1 mm與10 mm處溫度差隨時間變化曲線Fig.5 Change of temperature difference between 1 mm and 10 mm below the liquid surface with time

根據模擬計算得到的溫差，對實驗得到的液面下10 mm處溫度值進行計算，預測液面下方1 mm處溫度，計算溫度修正項系數κ，如圖6所示。從圖6中可以看出，下降趨勢消除，κ值在平均值0.559附近，其中位數為0.547，方差為0.019，因此κ值確定為0.559.

圖6 溫度修正后溫度修正基系數隨溫度變化曲線Fig.6 Temperature correction coefficient versus time after temperature correction

3 液柱實驗

3.1 驗證實驗簡介

使用200 mL乙醚，在一定孔徑的管中下流至容器內，下流距離為0.2 m，在一定風速的風道中進行實驗，實驗裝置如圖7所示。將液體倒入過濾杯中，通過0.2 m長不銹鋼管后流出，通過200 mm高風道進入盛料桶中，風道內風速為1.5 m/s. 使用風速傳感器控制風道內風速，使用溫度測試儀分別測量實驗前和實驗后的液體溫度，精度為0.02 ℃.

圖7 不同直徑液柱質量損失實驗裝置Fig.7 Experimental equipment for liquid mass loss at liquid columns with different diameters

通過控制不銹鋼管的內徑控制液流直徑，選擇內徑分別為1 mm、2 mm、3 mm、4 mm和5 mm的不銹鋼鋼管進行實驗，制造對應直徑的液柱。實驗得到液流持續時間和液體前后溫度差值，通過與計算值的對比，判斷本文所給出液體揮發速率計算模型的準確性。

3.2 實驗結果

表3中列出實驗驗結果，從中可以看出隨著直徑的增大，液流持續時間越長，損失質量不斷變小，溫度差不斷變小。

根據動量定理和動能定理計算理論初始下落速度，液體通過200 mm長垂直不銹鋼管的初始下落速度為1.4 m/s. 表3中通過對液流持續時間進行計算，得到初始下落速度，各液柱直徑條件下初始下

表3 液柱表面液體揮發實驗結果Tab.3 Experimental results of liquid evaporation on liquid columns

落速度均小于1.4 m/s，且隨著直徑的增大初始下落速度不斷變大。分析其原因，管直徑越小，液體流動受其壁面影響越大，因此直徑越大、速度越快，且小于理論值。

3.3 實驗結果與計算結果對比

對一定直徑液柱周圍空氣流場進行數值模擬，風道內空氣流速為1.5 m/s，得到周圍各方向的空氣流速，液柱直徑選擇1 mm、2 mm、3 mm、4 mm和5 mm，結果如圖8所示，在背風面風速很小，側風面風速最大，各直徑液柱周圍平均風速分別為1.18 m/s、1.05 m/s、0.97 m/s、0.93 m/s、0.83 m/s. 圖8中，h0、he分別為初始下落高度、最終下落高度，Δh為高度差，T0為液體流出不銹鋼管時液體溫度，ue為終點時下落速度，Te為下落終點時液體溫度，d為液柱直徑。

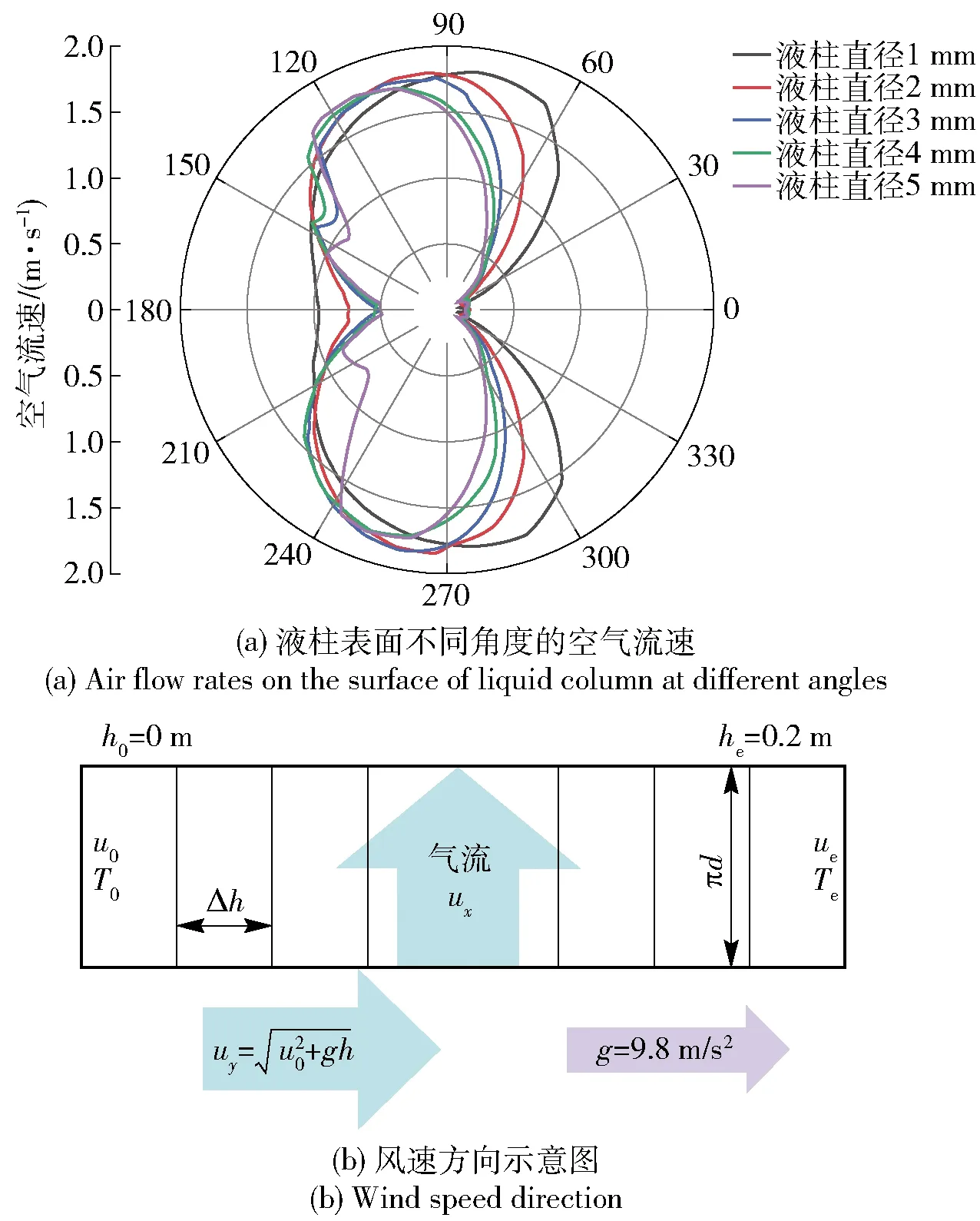
圖8 不同直徑液柱周圍空氣流速Fig.8 Air flow rates around liquid columns with different diameters

如圖8所示，液柱下流速度與空氣流速呈垂直方向，因此速度計算方法為

(10)

式中：ux為液柱周圍與風道底面平行方向的平均空氣流速(m/s)。根據實驗結果，在表3中列出不同直徑液柱條件下初始下落速度。液柱下落過程中液體揮發，吸收熱量溫度下降，因此溫度隨高度的下降降低。溫度變化率與液體揮發量呈正比，因此能夠得到計算公式：

(11)

式中：Ev為液體蒸發焓(kJ/mol)；cp為比熱容(J/(kg·K))。

(12)

解1階微分方程，得到T的計算公式：

(13)

式中：ω為溫度變化計算系數；Γ為溫度初始常量。根據表3給出的初始溫度及最終溫度，計算得到ω=26.96和Γ=272.87，h=0 m時對應初始溫度，h=0.2 m時對應最終溫度，計算結果在表4中列出。由表4可見，計算值與實驗值基本吻合，誤差最大為3.81%，這是因為液柱較粗時實驗過程較短、揮發量小，溫度變化小，測量相對誤差增大。液柱直徑小于等于3 mm時誤差較小，均在3%以內，這是因為液體溫度測量是在盛料桶中進行的，環境溫度高于液體溫度，液體與環境發生熱傳遞，導致實驗測量的液體溫度差偏低。計算值與實驗值誤差不超過4%，可認為本文計算模型準確。

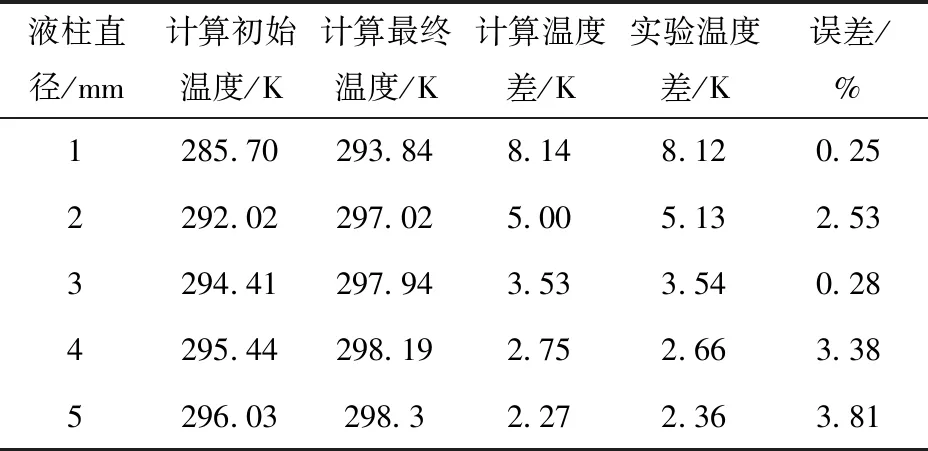
表4 溫度計算值與實驗值對比Tab.4 Calculated and experimental values of temperature

4 結論

本文通過實驗研究了不同風速及溫度對高揮發性液體氣液傳質速率的影響規律，得到相關結論如下：

1)隨著風速的增加，液體揮發速率增大，這一現象與已有理論相符。

2)隨著溫度的升高，揮發速率不斷增大，這一結果與已有理論相反。

3)以已有公式為依據，建立高揮發性液體傳質速率理論，得到修正后液體揮發速率計算公式，液體揮發速率與風速的0.78次冪呈正比，與溫度呈正比；經過液柱揮發實驗，證明公式計算準確性好，計算精度高。