永磁同步發電機模型預測直接轉矩控制方法研究
劉國聯
(湖南鐵路科技職業技術學院,湖南 株洲 412000)
0 引 言
目前,常用的幾種永磁同步放電機(Permanent Magnet Synchronous Generator,PMSG)的作業原理主要依靠直接扭矩控制和矢量控制[1-2]。相比之下,前者更為容易實現,所以如何合理應用算法提高電機直接轉矩控制預測精準度成為了重點研究內容[3]。
1 PMSG傳統控制算法分析
1.1 傳統控制算法概述
傳統控制算法建立在同步旋轉坐標系上,模型如下:
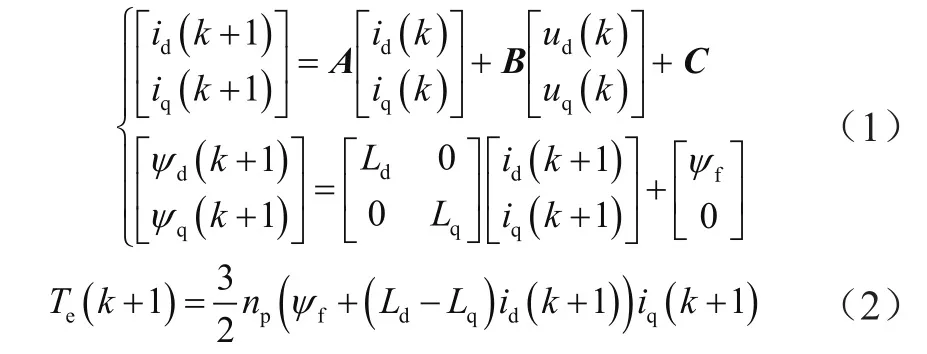
其中,id和iq分別代表定子電流在電機同步旋轉過程中沿著d坐標系、q坐標系方向產生的分量;ψq和ψd分別代表定子磁鏈沿著d坐標系、q坐標系方向產生的分量;uq和ud分別代表定子電壓在電機同步旋轉過程中沿著d坐標系、q坐標系方向產生的分量;k代表電機運行時刻;ψf代表永磁體磁鏈;Lq和Ld分別代表位于q軸和d軸的電感;np代表電機極對數;x(k+1)代表電機在k+1時刻下作業產生的轉矩變量。A、B、C均為矩陣,用于確定同步轉速、采樣周期等參數。在實際應用中,此算法暴露出動彈響應慢等問題。
1.2 傳統控制算法缺點
依據前文概述可知,PMSG傳統控制算法需要建立在同步坐標系上計算轉矩控制數據。該算法在先后改進過程中,分別暴露出計算量大問題、電壓矢量變化依附性問題。從理論層面分析,后者計算量有所減少,符合電機轉矩控制計算預測需求,但是7個電壓矢量的變化,同樣增加了算法運算量,對電機動態響應速度的提升幫助不大[4]。在實踐應用中,傳統控制算法參數依賴性過強,并且存在嚴重的魯棒性。因此,改進PMSG控制算法策略仍需深入探究。
2 PMSG控制算法的改進
2.1 算法改進總體方案
對于傳統控制算法存在的不足,本文利用全階滑模觀測器,對算法進行了改進,在靜態坐標系上形成了新的控制算法體系,即MP-DTC控制算法。圖1為MP-DTC控制算法框圖。
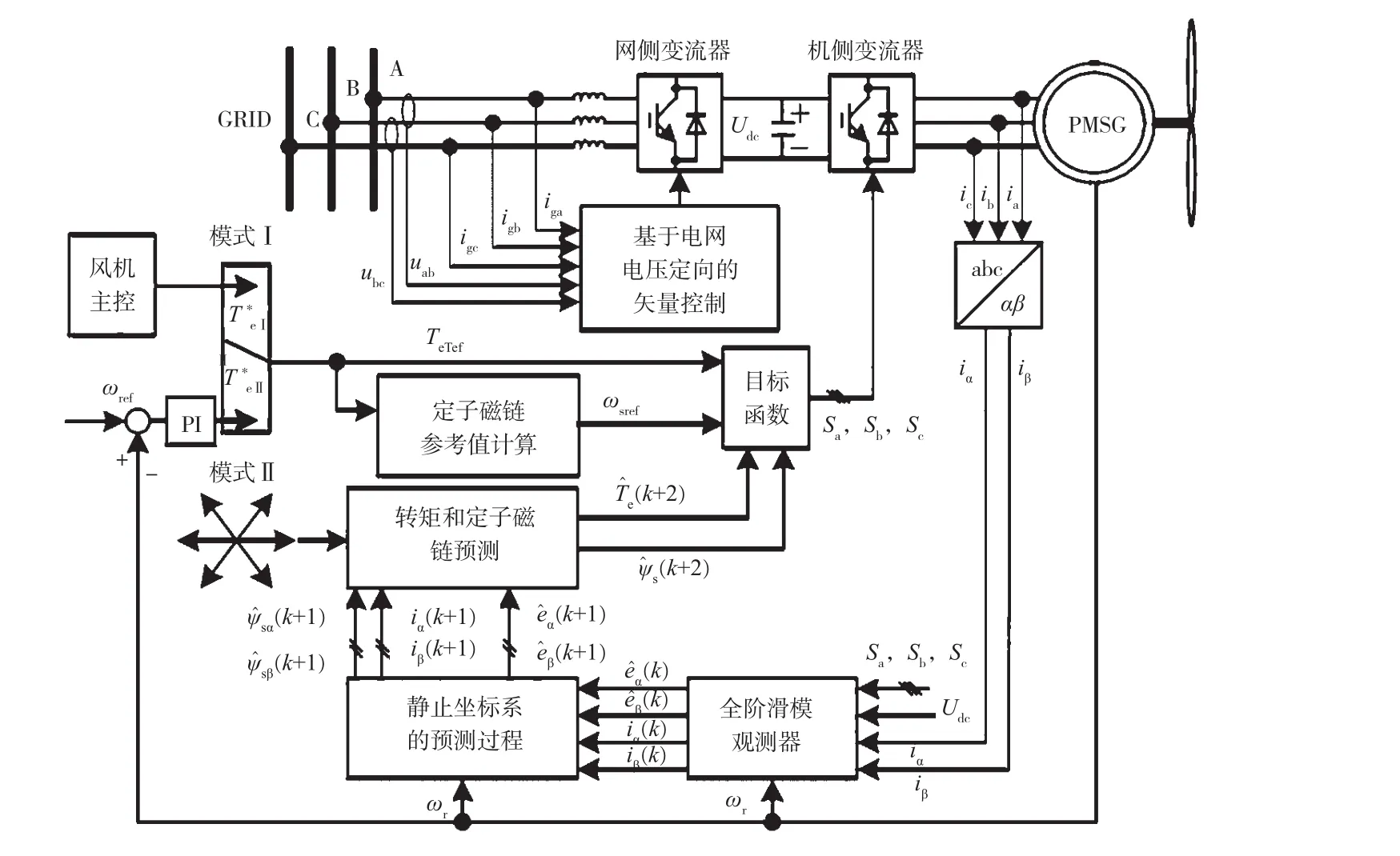
圖1 MP-DTC控制算法框圖
圖1中設定了兩種電機控制模式,模式Ⅰ相對簡單,通過計算定子磁鏈參考值,構建目標函數,在網側變流器和機側變流器作用下,對PMSG作業控制進行預測。模式Ⅱ在對轉矩和定子磁鏈進行預測的同時,增加了靜置坐標系的預測,引入全階滑模觀測器進行處理,形成新的目標函數,同樣網側變流器和機側變流器作用下完成預測。該控制算法不依賴參數設置,兩種模式應用在不同情況下預測,不僅可以彌補傳統算法的不足,還可以盡可能減少計算量,提高動態響應速度。
2.2 全階滑模觀測器的應用
本文提出改進算法的核心為全階滑模觀測器,利用該設備觀測電機的電磁轉矩和定子磁鏈。通過分析電機作業原理中的等效電動勢特點,在靜止坐標系上構建預測模型。
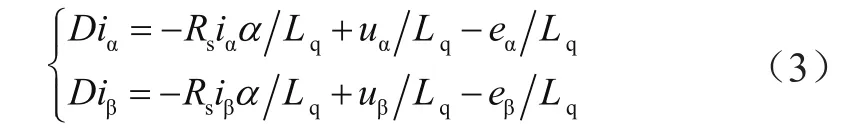
其中,eα和eβ均為等效反電動勢;D代表微分算子。
關于全階滑模觀測器的構建,本文直接引用研究比較成熟的模型體系,即文獻[4]的全階滑模觀測器。利用符號函數,計算觀測器的增益等參數數值,估算等效反電動勢,代入公式(4)進行計算,能夠得到電機正常作業下的定子磁鏈預算值。
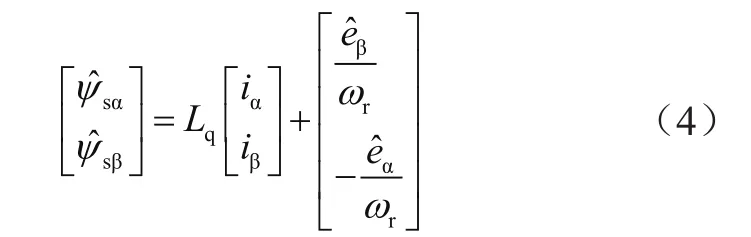
關于電機正常作業下的電磁轉矩預測計算公式如下:

其中,代表電磁轉矩預測結果。
2.3 靜止坐標系預測方案
本文采用前向歐拉算法,對靜止坐標系上的預測模型,即式(3)采取離散化處理,通過調節電纜和電阻2個參數數值,以減小外界因素影響,使得預測精準度得以提升。將預測得到的轉矩數值和定子磁鏈數值代入公式(6)中,得到電機的最優電壓矢量。

將最優電壓矢量作用于逆變器,從而實現PMSG預測控制。該算法功能實現具體流程如下。
第一步:構建滑膜觀測器模型,根據當前PMSG正常作業情況下各項參數數值,計算反電動勢。
第二步:對靜止坐標系下的模型采取離散化處理,結合反電動勢數據,預測電機運行k+1時刻下的定子電流數值。
第三步:依據反電動勢和定子電流數值,計算同一時刻下的定子磁鏈。
第四步:采用電壓矢量選擇方法,依據電壓分量和電壓矢量,預測下一個時刻的分量等參數值。
第五步:將第四步的計算結果代入式(5)中,得到電磁轉矩預測結果。每一組數值預測方法相同,根據矢量組別劃分情況,得到相應組數的預測結果。
第六步:將前兩個步驟計算得到的轉矩和定子磁鏈結果代入目標函數中,求取目標函數值最小情況下的電壓矢量。
第七步:將第六步計算結果作為電機作業的最優矢量,以此控制PMSG。
通常情況下,備選的電壓矢量數值為4個或者7個,需要根據實際情況計算數值,得到最優矢量。
3 測試分析
3.1 測試參數的設定
本文將兩種算法均應用至PMSG控制中,通過模擬仿真應用結果,得出判斷結論。表1為永磁同步發電機測試參數的設定情況。

表1 永磁同步發電機測試參數的設定
按照表1中方案設定PMSG參數,分別開展轉矩和轉速測量實驗。其中,轉矩的測量實驗是對參數突增情況下傳統算法與改進算法穩定性能進行測試,轉速測量實驗是對傳統算法與改進算法動態響應耗時進行測試。
3.2 測試結果分析
按照設計的測試方案,分別對參數突增情況下傳統算法與改進算法穩定性能、傳統算法與改進算法動態響應耗時進行測試,得到圖2和圖3對比實驗測試結果。
圖2左側圖為傳統算法應用下的PMSG的轉矩穩定性能測試結果,右側圖為本文提出改進算法應用下的PMSG的轉矩穩定性能測試結果。通過對比生成的穩定性能曲線可知,本文提出的改進算法轉矩測量穩定性更高一些,生成結果更加可靠。
圖3左側圖為傳統算法應用下的PMSG的軟件執行時間,右側圖為本文提出改進算法應用下的PMSG的軟件執行時間。很明顯,改進后的算法軟件執行耗時較短,上升沿代表作業狀態,改進后的算法軟件執行耗時縮減了24.4 μs,動態響應更加靈活。

圖2 參數突增情況下傳統算法與改進算法穩定性能測試結果

圖3 傳統算法與改進算法軟件執行時間對比圖
4 結 論
本文以永磁同步發電機作為研究對象,針對傳統算法在預測轉矩控制方面存在的動態響應不夠靈活、轉矩測量不夠穩定問題,引入全階滑模觀測器,提出新的預測算法。測試結果表明,改進后的算法達到提高了轉矩測量穩定性及靈活性,可以作為PMSG轉矩控制預測工具。

