基于“四個理解”的高中數學教學設計
陰瑞玲 薛亞云

摘要:本文從“四個理解”出發:理解數學,準確定位課時目標,把握極坐標思想的內涵與外延;理解教學,設置類比的教學方法,引導學生親歷探索圓的極坐標方程;理解學生,基于高二學生的知識經驗逐步成熟,引導他們主動探究;理解技術,運用視頻、PPT、幾何畫板幫助學生更好的理解極坐標方程。
關鍵詞:四個理解;圓的極坐標方程;類比思想
中圖分類號:G633.6 文獻標識碼:A文章編號:1992-7711(2020)12-088-1
章建躍博士提出理解數學,理解學生,理解教學,理解技術概括為“四理解”,這就是我們教學的總指導。理解數學是解決“教什么”的問題,理解學生是為了解決“怎樣教”的問題,理解教學就是解決“為什么這樣教”的問題,理解技術就是要解決“用什么促進教”的問題。
一、基于“四理解”確定教學目標
本節課是高中數學4-4《坐標系與參數方程》選講中第一講第三節的內容,是在復習了平面直角坐標系,引入了極坐標系,以及掌握了極坐標與直角坐標的互化的基礎上進一步學習《簡單曲線的極坐標方程》,并且學生已經學習了解析幾何與三角函數知識,對這節課的學習有一定的自主學習能力。這節在教參中的建議是2課時,本節課是第一課時。基于此,在理解教學和理解學生的基礎上,圓的極坐標方程這一節的教學目標設計如下。
1.知識與技能目標
理解極坐標系下曲線與方程的關系,會求圓的極坐標方程,掌握圓的極坐標方程與直角坐標方程的互化,體會極坐標系下求點的軌跡方程。
2.過程與方法目標
通過教學,使學生體會類比,從特殊到一般及整體思想,進一步認識數形結合在數學中的重要性。
3.情感態度與價值觀
培養學生觀察,分析與推理,探究的能力以及獲取知識的學習意識,激發學生的興趣和熱情,獲得積極的情感體驗。
二、基于“四理解”設計教學環節
1.引入環節
播放百歲山礦泉水視頻,講述廣告背后蘊藏的故事情形,引出笛卡爾的心形曲線,研究方程ρ=a(1-sinθ)的結構特征,引出課題,不僅將數學文化滲透其中而且極大地調動了學生們的學習熱情。
2.探究環節
(1)曲線的極坐標方程,基于高二學生知識經驗逐步成熟,有一定的類比歸納推理能力這一認知特點,讓學生自己類比直角坐標系曲線方程的概念推導極坐標系下曲線的方程,并且適時給出反例ρ=θ說明兩者的不同,進一步深刻的理解了極坐標系下極角的多值性,從而學生自己通過類比得出了定義,很好的詮釋了波利亞所說“類比和反例是獲得發明的偉大源泉。”
(2)求曲線的極坐標方程,學生仍然類比直角坐標方程得出求極坐標方程的五步,充分調動學生的主動性,切實體會極坐標方程是曲線方程的另一種表征方式,拓寬了學生的視野。
3.應用環節
圓的極坐標方程
應用1:求圓的極坐標方程
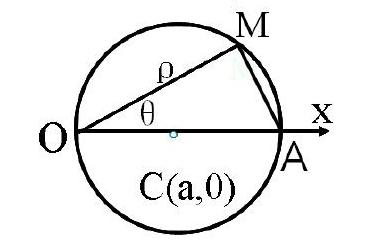
例1:如圖,已知圓心在C(a,0),半徑為a,求圓的極坐標方程。
學生們交流課前導學案的預習結果,生成了4種方法:
教學時重點突出極坐標的思想,原理,以教材提供的資源著重演繹極坐標思想方法。一題多解拓寬學生思維廣度,激發學生在解決問題中創新思維,式形結合從而達到研一題,悟一法,通一類的目的,為后面的學習在知識上和經驗上奠定了基礎。
變式訓練:若圓心坐標為M(ρ0,θ0),圓的半徑為r,求圓的方程.
基于例1的學習學生很快就給出了結果,r2=ρ2+ρ20-2ρ·ρ0cos(θ-θ0),當ρ0=r時,ρ=2rcos(θ-θ0)就是圓心在(r,θ0),半徑為r的圓的極坐標方程。特別的當θ0=0,θ0=π2,θ0=π,θ0=3π2時即為我們前面研究的圓心在特殊位置的圓的極坐標方程,在這里體會由特殊到一般再由一般到特殊的研究方法。
應用2:圓的極坐標方程的轉化
例2:已知一個圓的方程是ρ=53cosθ-5sinθ ,求圓心坐標和半徑。
學生們利用直角坐標和極坐標的互化,化成直角坐標系下求解圓心和半徑,強調互化中忽略自變量的范圍發生不等價變換。部分學生對極坐標系的運算往往通過直角坐標的轉換來運算,對于它的應用則淺嘗輒止,極坐標沒有變成一個學生解決問題的工具,而變成一種負擔,這和新課標引入極坐標的初衷不符,所以教學中應強化極坐標系應用意識,順勢引導學生在極坐標系下處理問題,將原式化為ρ=10(cosθ·32-sinθ·12)=10cos(θ+π6),所以圓心為(5,-π6)半徑為5的圓。
綜上所述,在“四理解”的指導下,教學自然、有序、高效,學生在學習過程中進一步中體會了類比,等價轉換,數形結合,整體分類等數學思想,重溫多種數學思想方法的美妙,極坐標不僅可以用另一種視覺看數學問題,開闊數學思維空間,而且提高學生對于數學應用意識的認識和理解。
[參考文獻]
[1]中華人民共和國教育部.普通高中數學課程標準(2017年版)[M].北京:人民教育出版社,2018.
[2]宮前長.新課程極坐標方程教學困惑、解惑與感悟[J].教學參謀,2015(19):58-62.
[3]徐小琴,趙思林.基于“四個理解”的數學教學[J].數學教學通訊,2018(2):5+29.
注:本文系山西省教育科學“十三五”規劃2019年度課題“基于四理解的高中數學教學設計的實踐研究”(編號GH-19360)階段性研究成果。
(作者單位:山西省太原市第五中學校,山西 太原 030012)

