基于博弈論賦權對銀行經營績效的動態評價

王彥偉

(安徽大學 安徽 合肥 230000)

一、理論介紹

(一)改進后的層次分析法(AHP)

一般的層次分析法具有很大的缺陷是當在變量很多的情況下，層次分析法判斷矩陣難以得到保證，需進行多次的一致性檢驗，導致計算量巨大，而且在用整數和倒數表示指標的重要性也難以做到完全客觀和準確，因此我們采用3標度的方法對傳統的層次分析法進行改進，能夠有效地避免決策者的主觀意愿帶來的誤差，提高準確性。

1.建立比較矩陣

我們對一般的層次分析法中的對所有指標進行比較后進行打分進行改進，對倆個變量進行比較，用3標度方法建立比較矩陣：

2.計算重要性排序指數

3.構造新的判斷矩陣B

B=(bij)n×n

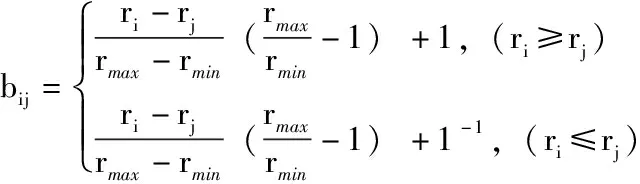
4.傳遞矩陣：M=(mij)n×n，mij=lgbij

6.擬優一致矩陣：R=(rij)n×n，rij=10dij

7.計算權重：求R的最大特征根所對應的的特征向量，進行歸一化處理，即為權重ω。

(二)改進后的熵值法(EVM)

1.判斷矩陣

假設我們收集到n個樣本，觀察每樣本的m維，得到樣本數據集X=(xij)n×m，針對各指標的量綱不同，利用下試對數據進行歸一化處理

則判斷矩陣為：

D=(dij)n×m,(i=1,2,…,n;j=1,2,…,m)

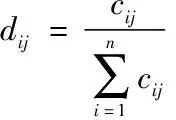
2.計算指標的熵值

傳統的求熵方法得到熵值為：

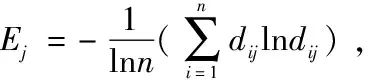
3.各指標權重向量W

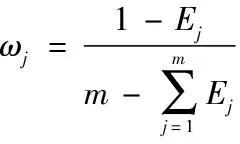
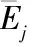
(三)組合賦權-博弈論組合賦權

本文采用綜合賦權的方法，基于層次分析法和熵權法，利用博弈論思想，進行綜合賦權，以科學的比例分配來平衡各個單一方法對綜合權重的作用。

假定采用了K種單一的賦權方法，記為ωi=(ωi1,ωi2,…,ωim),i=1,2,…,k，其中m表示選取的指標個數，則K種權重向量的線性組合可表示為：

根據博弈論的思想，即可以轉化為對單一權重向量的線性組合的優化，優化的目標為使得組合權重向量ω與各個單一權重向量的偏差達到最小，可用下式表達：

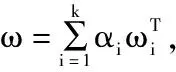
(四)時序加權平均算子(TOWA)

在動態綜合評價問題中，常采用時序加權平均算子對觀察年份進行賦權，最終形成指標權重與時間權重的集成，應用于對問題的綜合評價分析。

1.時序加權平均算子的定義

令N={1,2,…,n},[μi,ai]為時序加權平均算子對，μi稱為時間誘導分量，ai表示的是指標維度的數據量，定義時序加權平均算子為：

2.利用時序加權平均算子確定時間權向量

對時間賦權即為求時間權向量λ=(λ1,λ2,…,λp)T，本文采用規劃問題的求解方法來求解時間權向量λ=(λ1,λ2,…,λp)T。首先引入時間權向量信息熵I和時間度γ

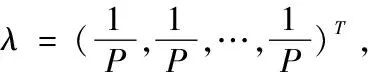
接下來我們求解規劃問題：時間權向量中各元素的差異最小。在給定γ值時，可轉化為求下面規劃問題的最優解：

二、實例應用

(一)數據的來源與指標體系的構建

本文依據2014～2019年國內13家具有代表性銀行的面板數據展開分析，分別包括5家大型商業銀行和8家全國性股份制商業銀行，這13家銀行的總資產占銀行整體資產的60%左右，在行業內具有較強的代表性。本文選取的指標數據均來自各大銀行的年報。

本文依據指標體系的構建原則，充分考慮指標的全面性原則、科學性原則、重要性原則、可得性原則[3]，建立如下的指標體系：

表1 13家銀行所構建的指標體系

(二)實例求解

建立如下的模型計算各銀行的綜合得分：

zki表示第k年第i個銀行的綜合得分，Zi表示第i個銀行綜合得分。

依據2019年13個銀行的截面數據，進行初步分析。本文采用全序列極差化法來消除指標量綱的影響，Xij表示消除量綱之后的數據。

依據改進后的層次分析法(法一)、改進后的熵值法(法二)和基于博弈論賦權(法三)對上述8個指標進行賦權，如下表

表2 不同賦權法結果

依據時序加權平均算子方法，由于對銀行的經營績效進行評價，則前期數據相對更具有代表性，因此選取時間度ω=0.4，采用Lingo軟件求解規劃問題，得到時間權重λ

表3 時間賦權結果

按照上述過程，對13家銀行的各個年份求綜合得分，以及對年份加權，得到13個城市的最終得分以及排名，結果如下表：

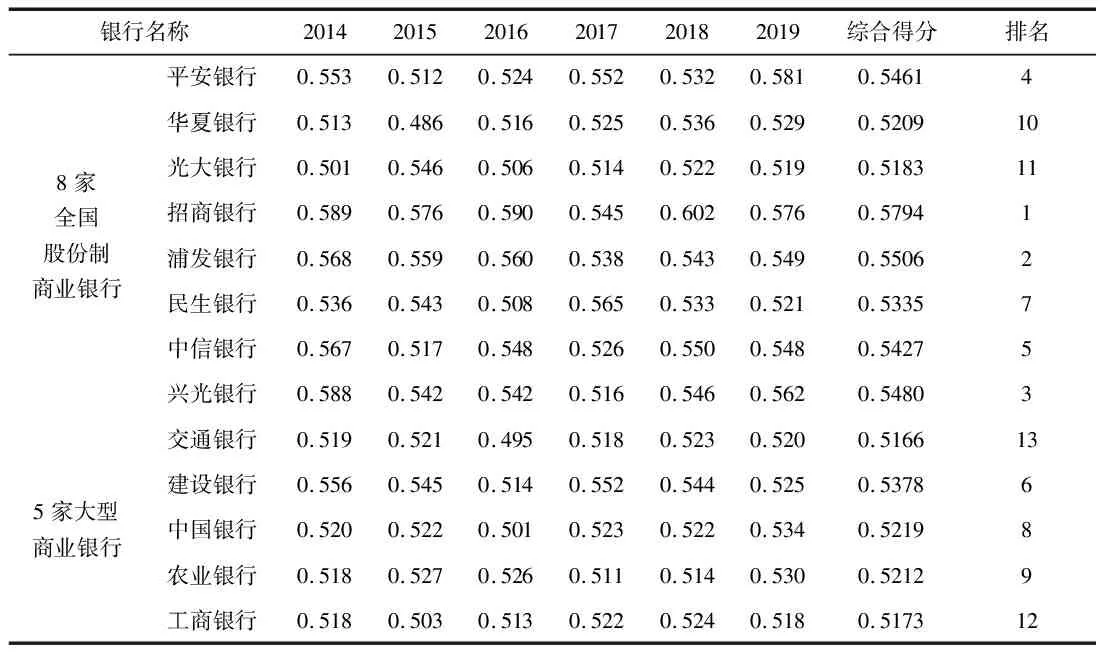
表4 2014～2019年13家銀行的得分及動態綜合得分與排名

三、結論

從上述結果來看，基本每股收益、存款增長率、營業收入增長率是影響經營績效的重要指標。8家全國股份制商業銀行整體績效要優于5家大型商業銀行。國有5大銀行實行的是一級法人治理結構下的多層代理體制，造成資產的管理有制度性的缺陷，在體制方面。遠遠落后于國外。在國有5大銀行中，建設銀行的排名最為突出，雖然建設銀行的成立時間較晚，由于在動態評價中，更注重前期的數據，所以其綜合得分較高，并且可以明顯的看到建設銀行在成長性和安全性方面明顯優于其他國有銀行，這與建設銀行近些年在自動化方面的投入息息相關。招商銀行作為我國目前最具有實力、規模最有優勢的銀行，在8家全國性股份制商業銀行中處于領跑位置，在盈利性、安全性、成長性表現強勁。