數學思維可視化工具的類型及其應用

沈利玲

摘 要?? ? 數學是一門具有高度抽象性邏輯思維的學科，對小學生來說難度較大。因此可以采取一些數學思維可視化工具輔助學習，通過量化的圖表更直觀地反應變量數值及變化過程，降低學習難度，同時拓展學生的思維空間。小學數學思維可視化工具分為思維地圖、思維導圖、概念圖三大類別。分析思維圖表對數學概念闡述的不同效果，以及對學生數學學習帶來的不同影響，可以為教師提供一定的參考借鑒。

關鍵詞? 小學數學 可視化工具 思維導圖 思維地圖

在數學學習的過程中，復雜的邏輯關系、主題與客體的相互作用共同催生了數學認知的思維活動。抽象的數學概念借助一系列具象載體和介質在主體的印象中形成新的認知。如何確保認知的準確性，提高數學學習的效率，降低認知難度，是檢測數學思維可視化應用的重要指標。數學的符號體系是一個完整而復雜的系統，各類符號和圖像之間都有著密不可分的邏輯關系。在小學階段的數學符號體系相對簡單，種類也有限，為了方便小學生理解應用，可以通過淺顯易懂的方式將抽象難懂的數學邏輯概念轉化成適合小學生學習的數學知識。可視化工具的衍生對數學學習者來說是便捷而快速的學習途徑之一，也是較為獨特的一種數學語言，不僅能夠提高數學學習效率，更能夠拓展學習思維，鍛煉學習者的探索能力。

一、思維地圖及其應用

思維地圖工具在1988年Expand Your Thinking一書中被首次公開提出，作為一種數學可視化工具，它的誕生使越來越多的教育工作者形成了新的知識體系構建途徑。思維地圖具有精準的概念闡述及類比功能，可對某一個晦澀難懂的知識點進行詳細闡述，并將多個相似概念放在一起類比，分析異同，研究各個概念間的相互關系，形成更為完善的知識體系框架。小學數學教學中常用的思維地圖包括以下幾種。

1.圓圈圖

圓圈圖是思維地圖中一種十分常見的表現形式，能夠鍛煉學生數學變式能力、數學推理能力及數學概念的概括能力，鍛煉學生對各類數學要素的協調能力，提高整體的數學思維能力。

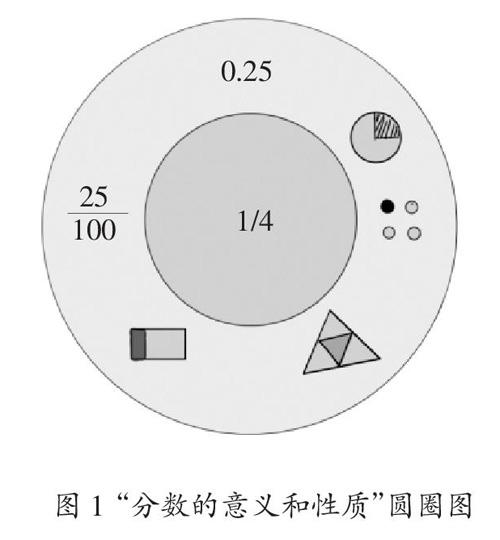
圓圈圖的繪制方法相對簡單，以某一個概念為中心，列舉同類對象。由于小學生思維模式較為簡單，所學內容也有限，因此可自由格式書寫，不限數量，盡可能地將能夠想到的抽象、具象的圖像符號與核心數學概念相聯系，在同一幅圓圈圖中加以體現。通過圓圈圖的直觀體現，分析各個對象的共同特征，得出這一概念的特征和性質。

以人教版《數學》五年級下冊第四單元“分數的意義和性質”為例，教師帶領學生初步認識分數的表現形式和含義后，可以鼓勵學生自己創作圓圈圖，在圓圈圖中盡可能地例舉的表現形式。例如統計中學過的餅狀圖，小數中學過的0.25，通分之后，以及多種幾何平面表現形式（圖1），充分發揮學生的想象力，鍛煉小學生的發散思維，使學生從多個維度進一步理解分數的意義和性質，同時鞏固所學知識內容。

2.氣泡圖

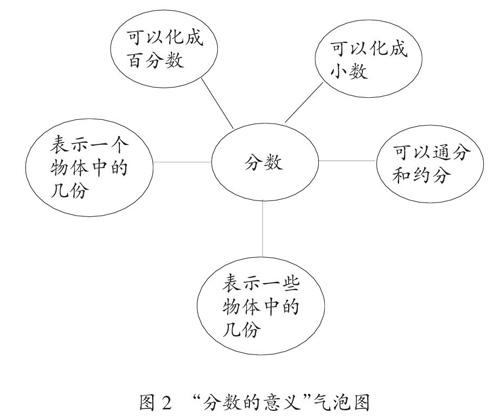
氣泡圖也是思維地圖中較為常用的一種表現形式，一般用來做發散思維訓練，總結某一個概念的各種特性。和圓圈圖不同的是，氣泡圖中每一個氣泡都可相互關聯又相互獨立，圍繞著核心概念形成一個完整而有邏輯的整體。氣泡圖能夠提高學生的發散思維能力，增強學生的分析總結能力，培養學生的學科素養，鍛煉學生的邏輯能力和探索能力。還是以人教版《數學》五年級下冊第四單元“分數的意義”為例，在學習這一課后，教師可要求學生繪制氣泡圖來檢驗學生的知識掌握情況。如圖2，是分數的氣泡圖，以分數這一核心概念為出發點，分散出五個特征概念：可以化成小數、百分數，表示一個物體中的幾份，也可以通分和約分，表示一些物體中的幾份。

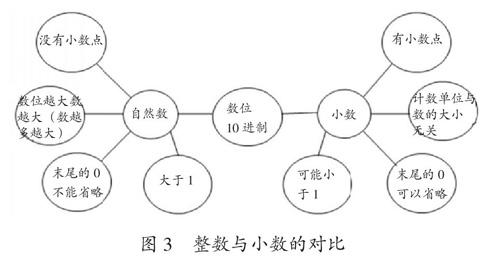
氣泡圖除了表現數學概念的特性，還可以用來對比兩個概念之間的區別及關系，探究二者之間的不同。在氣泡圖的眾多表現形式中有一種獨特的形式——雙泡圖。雙泡圖的產生源于對兩個相似概念的探究，輔助學生進行類比推理，通過對比兩個不同概念之間的聯系與區別，明確二者在應用過程中的相似性。學生在掌握了新概念之后，通過與舊概念的類比，得出二者之間的相同屬性與不同屬性。繪制雙泡圖，進一步探究兩個概念在數學學習過程中的不同應用模式與運用法則，同時也對二者做了合理區分，避免學生由于二者的相似之處產生思維混淆。圖3為雙泡圖所表示的整數和小數的特征區別，用于幫助學生歸納整理，區分整數和小數的特點，更加準確地完成數學學習任務。

3.樹形圖

樹形圖顧名思義，類似于樹狀，又名Tree Map，由一個頂端概念出發，由上到下分裂出數層分支，每個分支標明不同的概念，逐層分散解釋。樹狀圖的衍生主要是用于對知識體系的整理，使學生理解各類概念之間的包含關系。通常情況下，頂端的上位概念范圍比較大，末端的下位概念則屬于具體的小范圍概念，甚至是某一個具體的數值。

以人教版《數學》四年級上冊為例，圖4是這冊教材知識的樹形圖分析，將各單元打散重組，歸納整合，分為4個大板塊——數與代數、圖形與幾何、統計與概率、綜合實踐，各個板塊下面還有細分，如數與代數可細分為數的認識、數的運算、探索規律，數的認識下面可以列舉第一單元“大數的認識”，統計與概率中統計下面可列舉第七單元“條形統計圖”。對同一個大概念，每個人的思維體系不一樣，思維認知也不一樣，可以說，越是龐大的概念，每個人繪制的思維地圖就越是千差萬別。

4.括號圖

括號圖與樹形圖十分相似，樹狀圖為上下結構，括號圖則為左右結構，所表現的是部分與整體之間的邏輯關系。括號圖相比于樹形圖在形態上更加清晰，且從左到右的排列方式更加符合日常閱讀順序。

在人教版《數學》四年級下冊第五單元“三角形”的教學中，可以根據已經學過的幾何圖形繪制一張括號圖（圖5）。

括號圖不僅僅被應用于數學課程，在其他學科中也是常見的歸納模型。在小學數學中的應用，能夠幫助小學生塑造邏輯思維和系統歸納意識，化繁為簡，培養學生的學科素養，提高小學數學學習效率。

二、思維導圖及其應用

思維導圖是一種極富邏輯性和發散性的系統歸納方法，在數學學習過程中，合理地運用思維導圖能夠使小學生從小掌握分析能力，鍛煉他們的發散性思維和聯想能力，培養他們的分類認知。

思維導圖常常被應用在學科內容復習階段，更加注重學生知識體系的自主梳理和建構，鼓勵學生自主設計、自主羅列、自主學習，鼓勵學生獨立思考，親自參與對學科體系的建構過程，增強記憶。繪制思維導圖也是檢驗學生對學科內容知識的掌握情況的重要指標。除此之外，思維導圖還是學生自我評價的重要工具，數學課程標準指出：“在對學生的學習內容進行評估時，應該對學生的自我評估和相互評估予以保留”。思維導圖的誕生無疑是學生對學習內容最好的評價與反饋，透過思維導圖，我們能夠充分了解學生在數學學習過程中遇到的困難以及知識點的遺漏，使學生的知識體系和網絡得到進一步的完善。

思維導圖對學生學習方式也有一定的調節作用，通過思維導圖的繪制，學生能夠創造性地聯系各個知識模塊，主動思考各個知識體系之間的聯系，變被動為主動，更有利于培養學生的數學學習興趣。圖6為小學除法課程思維導圖示例。

三、概念圖及其應用

概念圖能夠有效地將課堂上較為抽象的、晦澀難懂的知識點變得直觀易懂，更加具體形象，便于學生掌握。小學階段的數學概念圖繪制，更加側重于不同概念之間的規律、聯系。數學學科的學習效果往往和學習興趣、學習熱情直接掛鉤，因此教師在數學教學過程中，應該注意對學生興趣的培養，利用概念圖化解數學概念的抽象性，降低數學學習難度，在潛移默化中使學生感受到數學的魅力。

在識圖階段，教師應該合理整合教學資源，不斷變換視圖方式，利用學生的好奇心，增強數學教學課程的趣味性，引導學生主動學習，提高學習效率，打造高效課堂。

在繪圖階段，教師要指導學生自主繪圖，并且強調繪圖質量，在保證學生能夠完整表達自己的知識體系的同時，盡可能地提高繪圖水平，使概念圖清晰明了，新舊知識點一目了然。這不僅能夠幫助學生鞏固知識體系，還能夠培養學生動手實踐的能力和創新性的思維模式。

除此之外，要注重對學生用圖意識的塑造，使學生在自主學習的過程中獨立完成概念圖的繪制工作，根據自己的知識體系呈現做自我反省檢查、查漏補缺，完善數學概念網認知絡。尤其是在復習階段，概念圖的知識體系能夠濃縮教材重點，化抽象為具體，指導學生針對自己的薄弱模塊加大復習力度，節約復習時間，提高復習效率。圖7為平面圖形相關知識的概念圖示例。

參考文獻

[1] 郭琳，楊培禾.小學數學復習中思維地圖的應用研究[J].首都師范大學學報：自然科學版，2017，38（04）.

[2] 史佳寧.思維地圖在小學數學思維能力培養中的應用[C].全國數學教育研究會.全國數學教育研究會2016年國際學術年會論文集.全國數學教育研究會：中國高教學會高等師范教育研究會數學教育會，2016.

[3] 費晴.用思維導圖助力學生構建小學數學單元知識體系[J].西藏教育，2019（12）.

[4]劉濤.淺談思維導圖在小學數學教學中的運用[C].廣西寫作學會教學研究專業委員會.2019年教學研究與教學寫作創新論壇成果集匯編（二）.廣西寫作學會教學研究專業委員會：廣西寫作學會教學研究專業委員會，2019.

[5] 盛文玲.思維導圖在小學數學高年段單元復習課中的應用[J].課程教育研究，2019（52）.

[6] 束佩芳.借助思維導圖，提升數學思維——以蘇教版一年級小學數學教學為例[J].數學教學通訊，2019（34）.

[7] 黃麗麗.思維地圖在小學數學教學中的應用研究[D].廈門：集美大學，2017.

[8] 俞娟.思維導圖在小學數學圖形與幾何復習課中的應用[C].中國智慧工程研究會智能學習與創新研究工作委員會.2019年教育信息化與教育技術創新學術論壇年會論文集.中國智慧工程研究會智能學習與創新研究工作委員會：重慶市鼎耘文化傳播有限公司，2019.

[9] 張海英.以圖融數，讓數學課程更美一些——小學數學課程與思維導圖的有效融合研究[J].小學教學參考，2019（32）.

[責任編輯：陳國慶]