小學數學教學中運算能力培養的途經與策略

迮恒良

摘要：學生運算能力的培養在數學教學中一直占據著重要地位，是學生整個數學學習階段乃至理科系列知識學習的重要基礎和工具，是數學研究的重點內容。《義務教育數學課程標準（2011年版）》是將“運算能力”作為十大核心概念之一提了出來。在實際教學中培養學生的運算能力，要在遵循兒童認知與發展規律的基礎上，注重算法和算理知識的掌握，注重數學知識體系的構建，注重數學思想方法的滲透，注重數學思維能力的培養和數學理性精神的弘揚，從而逐步提升以理性思維去解決數學問題的能力，達到有目的、有體系、扎實提升學生綜合素養的目的。

關鍵詞：算法和算理;知識體系;思維能力;理性精神;綜合素養

從建國初期的《小學算術課程暫行標準（草案）（1950年版）》到《義務教育數學課程標準（2011年版）》，學生運算能力的培養一直在數學教學中占據著重要地位，它是學生整個數學學習階段乃至理科系列知識學習的重要基礎和工具，是數學研究的重點內容。《義務教育數學課程標準（2011年版）》將“運算能力”作為十大核心概念之一提了出來，結合中國學生發展6大核心素養、18個基本要點中科學精神的基本內涵進行了具體的闡述。我認為，在遵循兒童的認知與發展規律的基礎上，培養學生的運算能力不僅要注重算法與算理的教學，還要注重學生數學知識體系的構建，注重數學思想方法的滲透，注重數學思維能力的培養以及數學理性精神的弘揚，從而有目的、有體系地提升學生的綜合素養。

一、注重算法和算理知識的掌握

算法和算理在計算教學中是相輔相成、密不可分的。算理是算法的重要根據，它指導著算法，而算法是算理的外在表現形式，它使算理外顯。教學時，如果只強調算理，則算法難以實現質的飛躍，如果只強調算法，則會導致學生“知其然，不知其所以然”。因此，在進行計算教學時，不但要關注算法，而且要關注算法背后的算理。教師要善于根據教學內容和學生的年齡特點、知識基礎等因素，綜合運用多種措施，幫助學生探明算理，掌握算法，發展學生的自主探究能力。

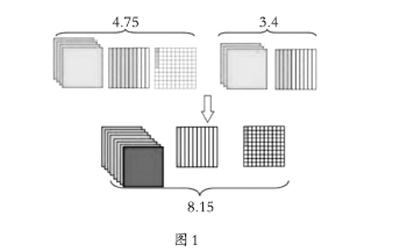
教學“小數加減法”中的例題4.75+3.4時，一位教師先讓學生自主思考，利用已有的生活經驗和知識儲備，自主探究個性化的算法，再交流各自的想法。學生有的用4元+3元=7元，7角+4角=11角=1.1元，5分=0.05元，7+1.1+0.05=8.15元;有的用3+4=7，0.75+0.4=1.15，7+1.15=8.15;有的將3.4的后面添上1個0變為3.40，讓每個加數都變為兩位小數，再列豎式計算;還有的直接將小數點對齊，列豎式計算……這樣，學生在探究的過程中體驗了方法的多樣化，他們比較了這些算法的共同點，再通過方格圖（如圖1），結合小數的意義來進一步理解了算理：可以先把4個1與3個1相加，再把7個0.1與4個0.1相加，滿10個0.1就向個位上進1，5個0.01直接移下來，結果是8.15。

著名教育家葉圣陶曾經說過：“教的法子要依據學的法子，學的法子要依據做的法子。”這位教師引導學生親歷自主探理的過程，并結合小數的意義，鼓勵學生展示真實的想法，在爭辯中悟理、明理，讓學生的智慧火花在碰撞中閃現;數形結合更是把抽象的算理直觀化、形象化、簡單化。“法”在交流中獲得，“理”在爭辯中明晰。學生沉浸在自主探究、獨立思考、交流爭辯的過程中，他們全程參與，悟透了小數加減法的算理，分析歸納出了小數加減法的計算法則，因而對算法與算理的理解和體會更加深刻，更容易內化為自己的知識。

二、注重數學知識體系的構建

《義務教育數學課程標準（2011年版）》中提出：“隨著數學學習的深入，學生所積累的數學知識和方法就成為學生的‘數學現實，這些‘現實應當成為學生進一步學習數學的素材。”選用這些素材，不僅有利于學生理解所學知識的內涵，還能夠更好地揭示相關數學知識之間的內在關聯，有利于學生從整體上理解數學，構建數學認知結構。因此，在教學時教師不但應該要讓學生知道怎么做，更應該讓他們明白為什么這樣做，并把新知納入到其原有的知識結構中，貫通新舊知識之間的內在聯系，直通數學本質，將學生的認知引向更深處。

教學“異分母加減法”時，學生通過紙上畫一畫，紙片折一折，透明膠片疊一疊，充分經歷了動手操作，自主探究，終得算理的過程，加深了對異分母加減法算理的理解。此時，應該趁熱打鐵，適時地去引導學生回顧以前所學的知識——整數加減法、小數加減法和同分母分數加減法是如何計算的，同一計量單位的兩種不同量又該如何進行加減的。教學中，可以引導學生通過舉例來呈現主要的思考過程，教師則相機板書：

15+43=？是怎樣計算的？

5個一+3個一=8個一

1個十+4個十=5個十

0.36+0.28=？是怎樣計算的？

6個0.01+8個0.01=14個0.01

3個0.1+2個0.1=5個0.1

[58]+[18]=？是怎樣計算的？

5個[18]+1個[18]=6個[18]

2米+8分米=？是怎樣計算的？

20分米+8分米=28分米

通過觀察，學生發現，所有加減法的計算都是在計數（計量）單位相同時，才能直接相加減。這是運算這一棵“大樹”的“主根”，大家以前所學的運算知識都是從“主根”上生長出來的“枝葉”與“花果”。要解決運算問題，我們就要順著“枝干”，想辦法回到“主根”上來汲取生長所需的營養，生長出一個個的“知識花果”，成就更加茂盛的“知識大樹”（如圖2）。

這樣，就能貫通各知識點之間的發展與聯系，形成知識體系，就能讓學生領悟知識背后的原理“主根”及化歸數學思想“主根”，從而在其腦海中形成一幅知識樹美圖。北京教育學院劉加霞教授曾經說過：“能否領悟和欣賞數學美是一個人數學素養的基本成分。”經常讓學生去構建這一類的知識美圖，發現數學知識本身之美，知識與知識之間的美，知識體系的美……學生的數學綜合素養就能在潛移默化中得到提高。

三、注重數學思想方法的滲透

“問題是數學的心臟，方法是數學的行為，思想是數學的靈魂。”不管是概念的建立，規律的發現，還是問題的解決，或是整個“數學大廈”的構建，歸根到底，其實是數學思想方法的建立。從這一基本意義上來說，數學學習其實不僅有具體數學知識的學習，也有數學思想方法的領悟。數學思想方法的領悟能促進學生在數學學習過程中，由對合理方法的“天才的、不自覺的運用”向“有意識的、自覺的運用”轉化，從而可以有效地指導我們的數學學習。

教學“異分母分數加減法”的第3課時，學生已經基本掌握了異分母分數加減的計算法則和一些基本的簡便運算技能，一位教師設計了一個練習題組：（逐條出示）

[12]+[14]+[18]=

[12]+[14]+[18]+[116]=

[12]+[14]+[18]+[116]+[132]=

…… ……

[12]+[14]+[18]+[116]+[132]+……+[11024]=

一開始，學生都無一例外地進行通分計算，但隨著數據越來越多，有些學生不動筆了，他們有的說：“分數越來越多，分母越來越大，用通分進行計算太難了。”有的說：“這一組題目不簡單，看起來應該是有規律的。”一語驚醒夢中人，很多學生這時也反應了過來，他們想：“對呀，這一題組中的數據有什么特征？存在什么規律呢？”經過一番探索之后，學生終于發現：所有分數的分子都是1，都是分數單位，后面一個分數的分母都是前面一個分數分母的2倍，后面一個分數都是前面一個分數的一半，每一道算式都是從[12]開始算起的，結果都是用1減去最后一個分數……

這樣，學生就發現了很多客觀存在的事實，并且他們還根據事實形成了猜想。但是，這個猜想對不對呢？這位教師不失時機地結合算式，畫出了一個正方形，作為單位“1”的示意圖。（如圖3）

在不斷等分的過程中，教師引導學生分析涂色部分、空白部分與整個正方形的關系。當等分到[116]的時候，很多學生恍然大悟：求涂色部分的面積和可以轉化成用整個正方形的面積減去空白部分的面積，即涂色部分的面積=1-空白部分的面積。這樣，前面形成的猜想就獲得了證明。當然，教師的教學并沒有止步于此，而是繼續引導學生思考：“如果像這樣不停地等分下去，最后所得的結果又會是怎樣呢？”這一問題把學生的思維帶入到了無限想象之中，滲透了極限思想。把數轉化成圖，直觀明了，正好應驗了華羅庚教授的那句名言：“數缺形時少直觀，形少數時難入微。”在這一教學過程中，教師成功地滲透了數形結合、抽象、類比、極限等數學思想，開拓了學生的眼界，讓數學學習變得更加簡單。

史寧中教授認為：“數學素養的培養是悟出來的而不是教出來的，會悟會看的底蘊是把握數學思想”。因此，在數學學習過程中，我們不僅要幫助學生夯實基礎知識、基礎技能，積累基本活動經驗，更應注意在掌握知識的過程中，了解數學知識的生成背景。要讓學生深入體會、領悟蘊含于數學知識發生、發展過程中的數學思想方法，從“有形”（具體的數學知識）中“觀”其“無形”（數學的思想方法）之妙，使學生真正深入透徹地理解與掌握數學知識，從而提高學生的綜合素養內容之一：數學文化素養。

四、注重數學思維能力的培養

數學是一門思維含量非常高的學科，它需要培養學生的邏輯推理、數學運算、空間想象、問題解決等能力，而如此眾多的數學能力均離不開數學思維能力。因此，培養數學思維能力是核心。運算教學時，教師要重視學生數學思維能力的培養，提升學生數學思維的能力，要讓學生自主、靈活地開展數學思維活動。在很大程度上，對學生數學思維能力的培養決定著學生數學學習的成效。

教學“分數四則混合運算”這一課時，學生通過大量例證、仔細觀察、慎密思考，得出了“分數四則混合運算的運算順序與以前所學的整數四則運算的運算順序完全相同”的結論。在鞏固練習環節，一位教師出示了這樣一組計算題：

[1120]×[57]+[1120]×[27]=

[38]+[57]+[27]+[58]=

[34]×[19]+[14]÷9=

[127]-（[13] ÷[715]+[45]）=

在教師出示的這一組題中，并沒有直接出現“簡單計算”或“能簡算就簡算”這樣的字眼，是直接讓學生獨立練習。這樣做就避免給學生一個暗示——這些題目有可能需要進行簡便計算。不直接要求簡便計算實際上比直接要求簡算更具有思維挑戰性。前兩題可以直接運用運算律進行簡便計算，而后兩題則要先算一算，在算的過程中，還需要根據實際情況進行簡便計算。換句話說，這些題目實際上都是可以進行簡便計算的。這樣的設計，不但要求學生正確地解決問題，還要求學生會根據題目的實際情況自主思考、自主選擇方法靈活解決。四道題目的難度依次越來越大，越來越不能一眼看出，有的題目甚至需要學生先根據運算順序算出一部分結果，再通過觀察數據特征，進行簡便計算。這樣的設計，讓能否簡便運算從很清晰、一眼看出，到有點模糊、需要算一算。這一系列由淺入深的思維活動促進了有效學習的發生。

教師在引領的過程中給學生搭建了思維的“腳手架”，讓學生的思維拾級而上，使學生順著“腳手架”步步深入地展開思考，訓練了學生思維的靈活性和創造性;“逼迫”學生注重自己思維的嚴謹性、嚴密性，考查了學生的觀察能力和數感，考驗了學生自主選擇方法、靈活運用知識解決問題的能力以及對事物的判斷能力。學生需要關注數據的特征，結合運算律和運算性質，選擇合適的方法進行計算。這是學生追求數學簡潔美的必經過程，可以讓學生的思維能力上升到一個更加理性的層次。這樣，也關注了思維背后的價值追求，對學生的成長非常有好處，為學生綜合素養的提升夯實了思維基礎。

五、注重數學理性精神的弘揚

當前，有一部分教師仍然認為，學生平時所學的數學就是為了考試而存在，所以應只注重數學技能的訓練;當然，也有一部分教師認為，數學的存在就是為生產實踐服務的，所以應只注重數學的實用性和工具性。日本數學家米山國藏曾經說過：“多數學生進入社會后，幾乎沒有機會應用他們在學校所學到的數學知識，這種作為知識的數學，通常在學生出校門后不到一兩年就忘掉了。然而不管人們從事什么業務工作，那種銘刻于大腦的數學精神和數學思想方法卻長期在他們的生活和工作中發揮著重要作用。”M·克萊因也認為：“數學是一種精神，是一種理性精神。”這些理論深刻揭示了數學理性精神教育的重要性。這就是說，相對于技能和工具，培養學生的數學理性精神才應該是數學教學的核心價值。思維受理性的感召，理性的思維依賴理性精神的支配，只有擁有理性精神，才能理性地思考問題。

教學“異分母分數加減法”第1課時，一位教師首先通過創設情境，讓學生列出算式：[14]+[12]。接著，教師引導學生觀察算式的特征，猜想算式的結果可能是[16]、[26]、[24]、[28]、[34]這五種，針對這些結果，學生自主思辨，他們很快發現：不可能是[16]，因為[16]比[14]、[12]都小;[26]也不可能，因為[26]=[13]，[13]本身就小于[12];[24]和[28]也不對，因為[24]就是[12]，[28]就是[14]，本身加上另一個分數肯定比自己要大。這樣，學生通過簡單的估算、推理，判斷出有一些猜想結果是錯誤的。然后，教師引導學生利用身邊已有的材料驗證[34]這一結果是否正確。學生獨立思考、分組驗證、交流分享。他們有換算成時間的，有轉化成小數的，有用透明膠片重疊的（畫圖法），也有通分的……自由的時空換來了思維“火山”的“迸發”，學生的各種新奇方法層出不窮，他們還發現通分法就是膠片重疊法（畫圖法）的算式化，所有方法都是把異分母加減法這一新知轉化成已經學過的舊知，從而驗證了猜想，獲得了結論。

縱觀數學發展史，古埃及人和歐洲人對分數加減法計算之繁瑣是望而生畏的，德國人甚至用“掉進分數里”的諺語來形容一個人所處的困境。而我們的祖先通過小小的算籌，發明了“齊同術”，完美地解決了這一難題，攀上了數學的“高峰”。本節課中，教師不但讓學生經歷了觀察、猜想、驗證、結論這一完整的、理性的科學探索過程，還讓他們體驗了分數加減法計算過程的艱辛，激發了他們對古人科學探索精神的崇敬。在課尾，教師還滲透了數學史的教育，讓學生感受到了我國數學文化的源遠流長，激發了學生的民族自豪感和責任感。這樣，在滲透愛國主義教育的同時，也提升了學生的綜合素養。

從畢達哥拉斯—柏拉圖的“傳統數量關系構成了現實的本質”，到經院哲學家們的“上帝按照數學模式創造了世界”;從歐氏幾何到非歐幾何，再到康托爾的無窮集合理論……數學史上的很多故事都體現出了數學的理性精神。它已經成為了數學家研究數學、研究世界的動力，同樣也應該是學生學習數學、研究世界最原始、最永恒、最有效的動力。當然，理性精神也不是一成不變的，它也是在不斷地發展和演化之中的。在平時的課堂教學中適當介紹數學史，展示數學知識的形成過程，可以讓學生感受數學文化之美和數學家嚴謹的治學精神，從而提升學生的理性思維能力。久而久之，學生就會逐步形成理性的思維精神。

總之，新時期的數學課程改革對小學數學的運算能力教學提出了更高的要求，上述的五個重點并不是完全獨立的，而是密切聯系的。因此，我們在教學中可以引導學生運用多種方法探明算理，獲得算法，內化數學知識體系，感悟其中蘊含的數學思想方法，逐步提升以數學理性精神和理性思維解決數學問題的能力，從而扎扎實實地提升學生的綜合素養。

參考文獻：

[1]中華人民共和國教育部.義務教育數學課程標準（2011年版）[S].北京：北京師范大學出版社，2011.

[2]鄭毓信.數學：看不見的文化——論數學的文化價值[J].南京大學學報，1994（1）.

[3]張先龍.數學教育要培養理性思維素養[J].中學數學教學參考，2017（9）.

[4]侯維民."數學精神"與數學教育[J].數學教育學報，2004（8）.

[5]張海進.打開兒童通住"理性世界"的大門[J].教育研究與評論，2014（6）.

（責任編輯：楊強）