利用線源入流測量方法對土壤入滲影響因素的研究

崔宇菲，李玉中，龔道枝，毛麗麗

( 中國農業科學院農業環境與可持續發展研究所，農業部旱作節水農業重點開放實驗室，北京 100081)

土壤水分滲透(或稱滲吸、入滲)描述的是水分進入土壤的過程，是水分循環的重要組成部分。由于入滲過程中土壤基質吸力梯度下降，土壤入滲速度隨時間按指數規律減小。水分在干燥土壤開始滲透時，基質吸力梯度比較大，水流滲入土壤的速度很快。隨著滲透的進行，濕潤土層逐漸加厚，吸力梯度逐漸減小并趨近于零。滲透速度除了隨時間變化外也受土壤的初始土壤含水率、地形地貌、植被覆蓋、土壤鹽堿化程度以及降雨強度和持續時間等的影響[1-2]。

土壤含水量尤其是初始含水率是影響水分入滲和傳導過程、改變土壤入滲速率的重要因子。土壤含水量對大田土壤入滲能力的影響主要表現在入滲的初始階段，土壤含水量較高時入滲濕潤鋒處的吸力梯度相對較小，因而入滲率也小；但土壤含水量較低時，濕潤鋒前沿處吸力梯度大、入滲率也大。較高的初始含水量會降低土壤的吸力梯度，土壤內部由于含有大量的水分，孔隙度也大大降低，這都會降低土壤的初始入滲性能[3-4]。研究不同初始含水量下土壤入滲過程有利于揭示降雨產流機制[5]，Hino等[6]利用人工模擬降雨研究[7-9]得到土壤入滲率與初始含水量具有非常高的相關性。賈志軍等[10]、王全九等[11]、解文艷等[12]、陳洪松等[13]、劉金濤等[14]、曹辰等[15]、劉汗等[16]分別在野外坡地或室內模擬環境下對土壤入滲模型參數及入滲過程與土壤初始含水率的關系進行了研究，得到隨初始含水率的增高初始入滲率減小的結論。張俊等[17]研究了初始含水量對新型地下灌溉方式——微潤灌的影響，解文艷等[12]研究了含水量為13.4%～32.7%之間的入滲過程，認為累積入滲量、穩定入滲率隨土壤初始含水量的增加而降低，王全九等[11]利用環刀法研究了含水量為2.25%～16.4%之間的土壤入滲過程，發現土壤飽和導水能力(穩定入滲率)隨初始含水率增加而增大。Hillel[4]發現土壤初始含水量對穩定入滲率的影響并不明顯。Hawke等[3]利用模擬降雨試驗研究發現土壤累積入滲量隨土壤含水量的增加而減小。雖然關于土壤初始含水量對入滲過程的影響研究很多，但迄今為止并沒有得到一致的結論。

地表坡度對土壤入滲過程的影響有很多研究。Singer等[17]和Mah等[18]發現地表坡度與土壤入滲性能沒有直接關系。Peosen[19]研究發現，坡度越大，雨滴打擊到地表的時候與地表的夾角越小，單位面積上對地表的打擊作用越小，導致地表結皮現象減弱，進而得出土壤入滲率隨坡度的增加而增大的結論。Janeau等[20]得出過類似的結論。Chaplot等[21]發現水流流速越快，地表水流深度越小，表明坡度越大，土壤入滲性能越低。Bobe[22]利用圓盤人工降雨器完成了三種土壤(砂土、壤土及粘土)在坡度5°、10°以及15°條件下的入滲試驗，發現坡度對土壤入滲過程沒有明顯影響。

綜上所述，迄今為止關于土壤初始含水量對穩定入滲率及累積入滲量、坡度對入滲過程的影響作用沒有得到一致的結論。當向地表的供水達到或超過土壤的入滲能力時，土壤的實際入滲等于土壤的入滲能力，這是測量土壤入滲能力的基本條件。現有的研究受測量方法的限制，在入滲測量初始階段很難滿足充分供水的條件，因此土壤入滲的初始過程測量不夠完整，不能準確揭示入滲過程影響因素、影響規律及其相互關系。同時，大部分傳統的入滲試驗測量方法對土壤有不同程度的破壞，得到的入滲過程綜合了很多的影響因素，單一因素(如初始含水量、坡度等)對入滲過程的影響很難分析出來，這也是現有的關于土壤初始含水量和地表坡度對入滲影響作用結論不一致的原因之一。由于土壤初始含水量影響降雨入滲、產流過程，所以對土壤水分沿坡面的分布具有重要的作用，同時坡面的水分分布情況也影響坡面降雨入滲、產流過程[8]。

Mao等[23]提出的土壤入滲性能線源入流測量方法，在整個土壤入滲性能測量過程中供水強度不小于土壤入滲能力，滿足了充分供水的條件。土壤入滲過程均由土壤本身的入滲能力控制，觀測得到的入滲率不受供水強度的影響，能夠反映土壤的入滲能力。從上述分析看出，土壤入滲過程的觀測方法是研究各因素對土壤入滲影響機理的基礎。本研究在提出的土壤入滲過程線源測量方法的基礎上進行室內試驗，研究土壤初始含水量和地表坡度對入滲過程的影響作用。由于測量方法本身的優勢，可以得到完整的入滲過程，因此對土壤初始含水量及地表坡度對入滲過程的影響作用分析更為完整和準確。在此基礎上，可以進一步分析其他因素對入滲過程的影響。

1 試驗材料與方法

1.1 試驗處理

本研究應用Mao等[23]提出的土壤入滲性能線源入流測量方法進行土壤初始含水量和地表坡度單一因素對入滲過程的影響研究。室內測量系統由土槽、布水器、供水裝置和測量裝置組成，具體見圖1。

圖1 試驗裝置模型圖Fig.1 The experimental apparatus

土槽的長、寬、高分別為1 m×0.6 m×0.25 m，沿寬度方向分為3個同樣尺寸的小槽作為3個重復。土槽的側面固定帶有刻度的標尺，用于記錄水流在地表推進的過程。

試驗所用土壤為壤土，其中砂粒(2～0.05 mm)占53%、粉粒(0.05～0.002 mm)占27%、黏粒(<0.002 mm)占20%。設置了三個土壤含水量水平，分別為風干土、8.22%和16.3%，風干土是將土樣從野外取回后直接在室溫下風干2個月，含水量維持在較穩定水平后再進行后續的過篩、配比含水量等處理，實驗室測量風干土的含水量數值為2.15%；設計供水強度分別為4.69、4.08 L·h-1及3.04 L·h-1；地表坡度設置為0°、5°及15°，設計供水強度分別為4.64、4.20 L·h-1及4.35 L·h-1。

1.2 試驗方法

試驗采用馬氏瓶恒壓供水，試驗過程中利用數碼照相機記錄地表濕潤面積的變化過程。

試驗先將土樣風干后過2 mm篩，在3個小土槽底部分別裝入一層1.5 cm厚的細砂，以形成透水透氣性能較好的邊界。將過2 mm篩的土樣稱重，并測定其初始含水量(2.15%)，按照設定的兩組初始含水量計算需要添加的水量。用噴壺將水均勻地噴灑在土樣上，混合均勻后用塑料布密封放置48 h，讓水分充分分布，以保證土壤內部含水率基本均勻。

按天然容重即1.26 g·cm-3將土樣每5 cm為一層分層裝入。土樣放入土槽后，在不搗壓的前提下用耙子整平，并在裝入下一層土之前先將前次裝入的土層表面用工具打毛，以避免上、下土層之間出現結構和水動力學特性突變等不必要的內邊界。總裝土深度為20 cm。土樣裝入后，將土槽調整到設定坡度進行試驗。

試驗過程中的具體觀測內容和記錄、計算數據如下：

(1)記錄時間間隔：由秒表控制，分別按1、2、5、10、15、30 min的間隔來記錄馬氏瓶讀數和拍照時間間隔；

(2)時段內累計入滲水量：記錄馬氏瓶上初始與結束時刻的刻度，計算得到時段內的累積供水量即時段內流入地表的水量；

(3)地表濕潤面積：首先由數碼相機拍攝試驗中地表濕潤過程照片，根據對應土箱兩邊的刻度記錄，由計算機處理計算得到時段內增加的濕潤面積。

(4)土壤入滲率的計算：根據觀測內容和記錄數據，應用Mao等[23]提出的計算公式，得到不同時間的入滲率為：

(1)

式中，q為供水流量(L·h-1)；i為入滲率(mm·h-1)；ΔA為時段內濕潤面積增量；n為對應的時段。

2 結果與討論

2.1 初始含水量對入滲的影響

設定的三個初始含水量條件下，土壤表面濕潤面積變化過程由照片記錄。將得到的照片加載到AutoCAD中，對濕潤面積在照片中的變形進行還原，計算得到地表濕潤面積推進過程見圖2。

根據濕潤面積隨時間增加規律，并考慮試驗最終得到穩定入滲率這一邊界條件，利用毛麗麗等[23]提出的擬合公式，將圖2中的數據利用式(2)進行擬合。

A=M(1-e-Nt)

(2)

式中，A為地表濕潤面積(mm2)；t為時間(min)；M，N均為擬合常數。

如圖2所示，在土壤入滲初始階段，地表濕潤面積隨時間增加很快。各擬合曲線的斜率在初始階段很大，隨著時間的推進慢慢降低并最終趨于一致。這說明初始含水量對地表濕潤面積增加的最終階段影響不大，擬合參數及每組擬合結果的確定性系數見表1。

表1 濕潤面積增加過程擬合參數

圖2 地表濕潤面積推進過程Fig.2 The wetted area as function of time

應用式(1)計算不同土壤初始含水量條件下的入滲率，得到的結果見圖3。

如圖3所示，3組不同初始含水量條件下的土壤入滲過程規律比較明顯。含水量8.22%的初始入滲率最高，風干土(含水量2.15%)的初始入滲率最低。隨著時間的推進，3組土壤的入滲率逐漸接近，3組穩定入滲率差別不大。Hillel[4]指出土壤初始含水量越高，初始入滲性能就越低，入滲達到穩定的時間越短。本研究中，初始含水量最高(16.3%)的土壤初始入滲率比含水量為8.22%的土壤低，符合Hillel提出的基本規律。這是由于初始含水量高的土壤吸力梯度較小，土壤孔隙也較少，因此水流進入土壤的過程比含水量低的土壤慢。同時，Levy等[24]指出，干燥土壤的快速濕潤過程會導致土壤團聚體的破壞及地表結皮的形成，進而會降低土壤的入滲性能。本試驗中風干土(2.15%)的初始入滲率比含水量最高(16.3%)的還要低，原因可能是快速濕潤導致地表出現結皮，進而降低了土壤入滲率[24]。由于應用其他傳統入滲測量方法過程中出現的地表結皮及雨滴對地表的打擊作用，導致土壤入滲過程的初始階段觀測不準確，無法準確分析土壤初始含水量對入滲過程初期的影響作用。本研究結果指出，風干土由于快速濕潤導致地表出現結

圖3 不同含水量條件下的土壤入滲過程Fig.3 The infiltrability functions for soils with different initial moisture contents

皮，降低了入滲率；初始含水量最高的土壤由于土壤吸力較小，初始入滲率也較低。本試驗中含水量居中(8.22%)的土壤初始入滲率最高，較高或較低的初始含水量均不利于水分在初始階段迅速地滲入土壤。

Philip入滲模型[25]是現今為止應用比較多的入滲模型，該模型具有明確的物理意義，首次提出利用數值方法解決土壤水流問題。Philip入滲模型的簡化公式為：

(3)

式中，i(t)為入滲率(mm·h-1)；S為土壤吸著力(mm·h-0.5)；t為入滲時間(min)；A為常數(mm·h-1)。

利用Philip入滲模型對試驗結果進行了擬合，如圖4所示，Philip入滲模型與本研究得到的結果擬合效果非常好。但模型擬合的穩定入滲率均比測量得到的低。

不同土壤初始含水量條件下，測量得到的土壤初始入滲率與Philip入滲模型擬合回歸得到的參數吸著力(S)具有相同的變化趨勢。如表2所示，初始含水量為8.22%的土壤擬合得到的初始入滲率比其他兩組含水量的土壤高。圖4中Philip入滲模型與測量得到的土壤初始入滲階段擬合很好，但對穩定入滲階段的擬合精度較差，擬合得到的穩定入滲率為負值。分析原因可能是Philip入滲模型公式中時間的指數設置為(-0.5)導致的。受該指數的影響，模擬過程中土壤初期的入滲率越高，擬合得到的穩定入滲率越低。由于傳統土壤入滲率測量方法受供水等限制，測量得到的土壤初始入滲率比較低，因此在利用Philip入滲模型進行擬合時，擬合結果反而比較好，不會出現本研究中的模型指數設置問題。

表2 Philip入滲模型擬合參數

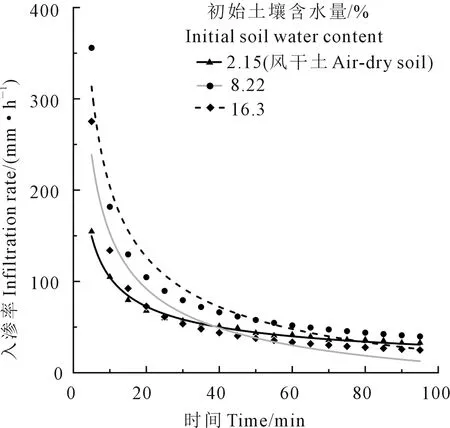
圖4 Philip入滲模型擬合結果對比Fig.4 The curves fitted by the Philip Infiltration Model

2.2 地表坡度對入滲的影響

三個不同坡度條件下，利用土壤入滲性能線源入流測量方法得到的地表濕潤面積累計增加過程見圖5。

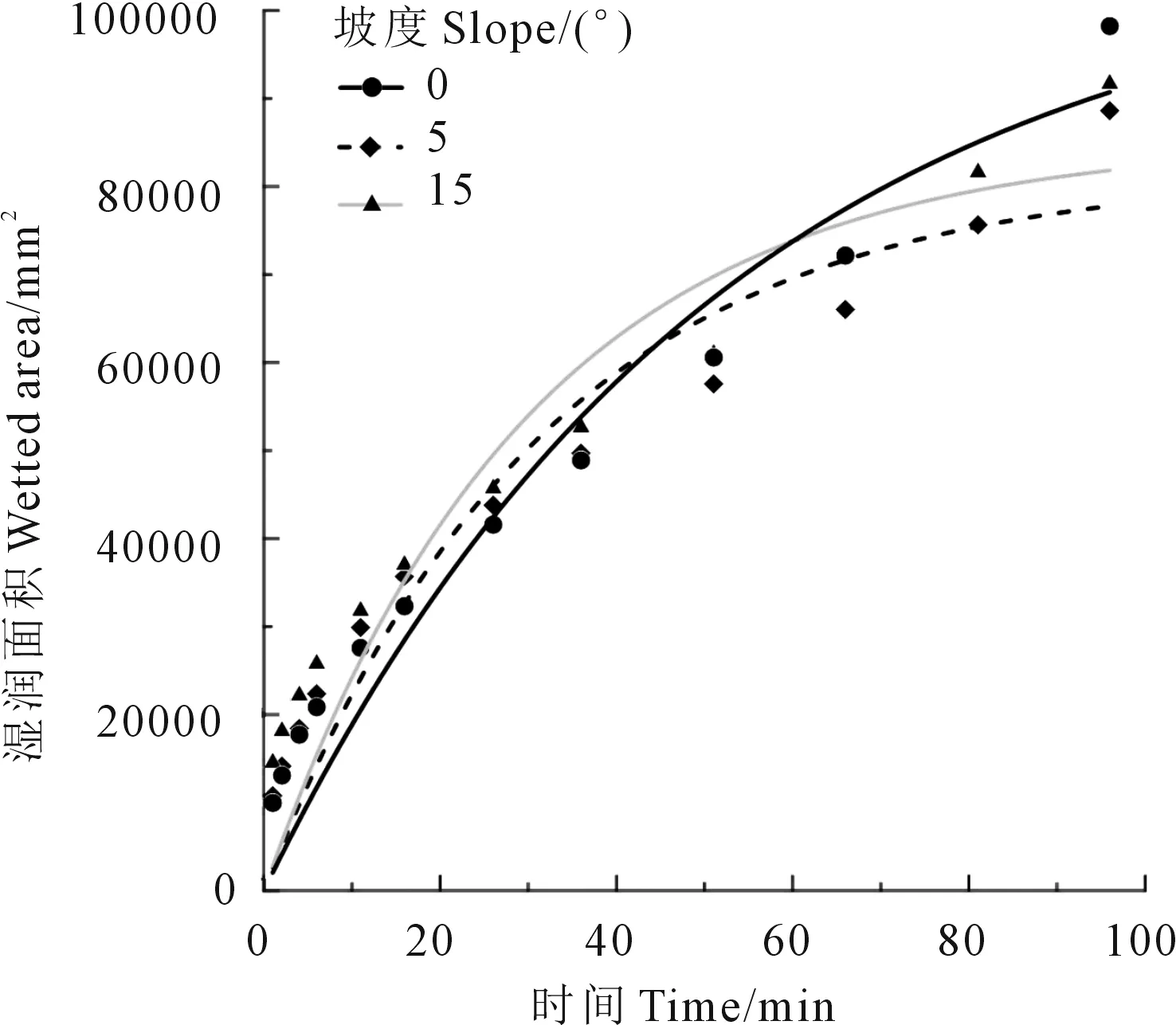
圖5 地表濕潤面積隨時間變化過程Fig.5 The wetted area as function of time

利用式(2)對地表濕潤面積推進過程進行擬合，具體擬合參數見表3。式(2)與測量數據擬合非常好，擬合確定性系數都很高(表3)。擬合結果中e的指數為負數，這表明隨著時間的推進，地表濕潤面積趨于一個穩定值，即擬合方程中的M，表明當入滲持續一段時間之后，地表濕潤面積將不再繼續增加，而是達到一個穩定值。入滲過程中的穩定入滲率可以直接從地表穩定入滲面積中估算，具體計算過程為：

表3 地表濕潤面積推進過程擬合參數

(4)

(5)

(6)

從上面的計算結果看，3種坡度條件下的土壤穩定入滲率非常接近。這表明坡度對穩定入滲率影響較小。土壤入滲率隨時間變化過程見圖6。

如圖6所示，3組不同坡度條件下的土壤入滲過程非常接近，并沒有明顯的差別。這表明坡度對土壤入滲過程的影響很小。Singer[17]及Mah等[18]通過試驗得到了與本研究一致的結論，即坡度與土壤入滲率沒有明顯相關關系。

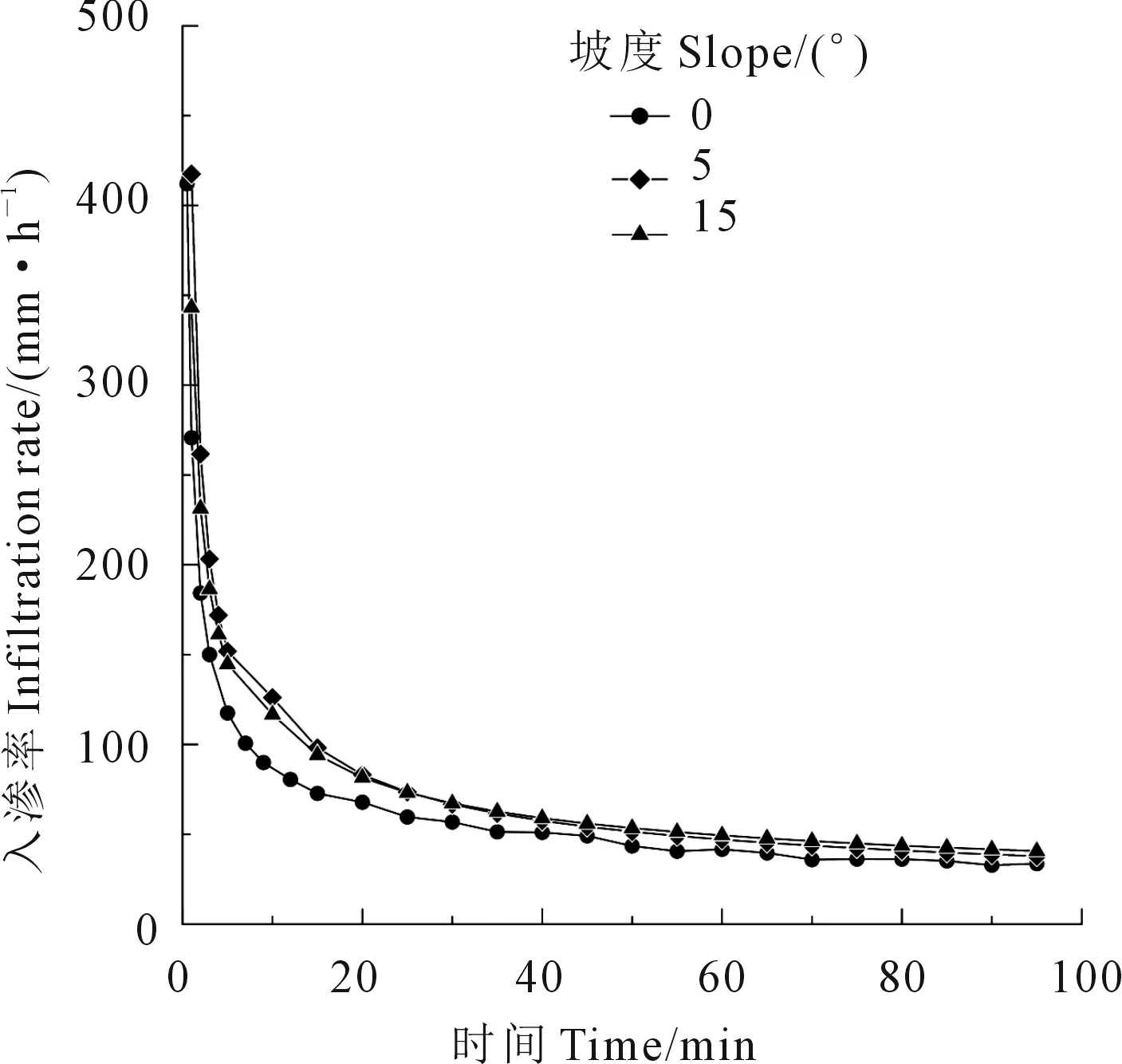
圖6 土壤入滲性能Fig.6 Measured infiltrability changing with time

利用Philip入滲模型對本研究中不同坡度條件下的土壤入滲過程進行擬合，結果見圖7。利用Philip入滲模型擬合得到的三種坡度條件下的土壤入滲率變化過程基本沒有區別，3組擬合曲線非常接近。具體擬合參數見表4。如表4中所示，擬合方程的確定性系數均非常高，這表明Philip入滲模型可以很好地描述測量的入滲過程。Philip入滲模型擬合得到的穩定入滲率(表4)與實際計算得到的穩定入

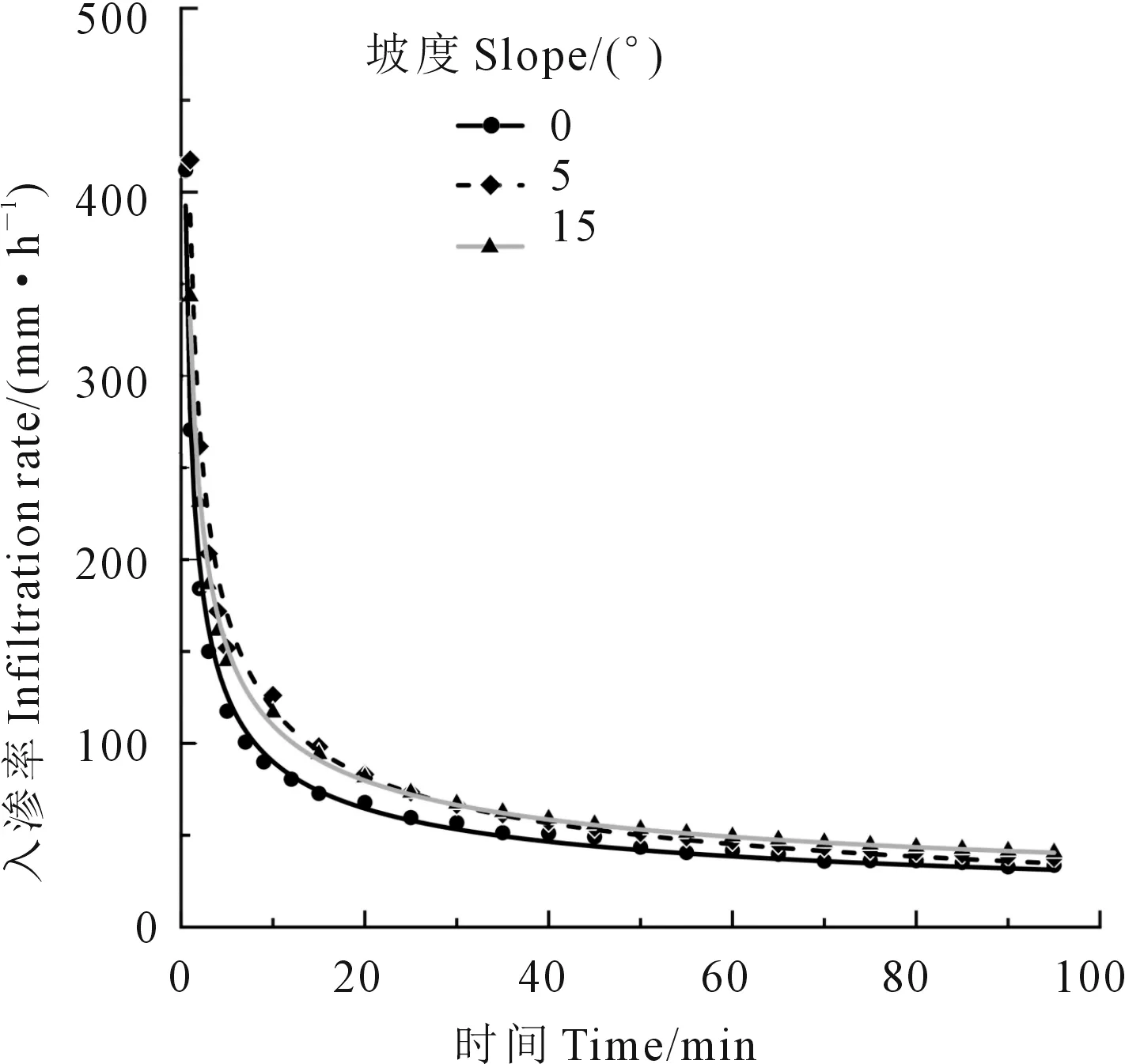
圖7 Philip入滲模型擬合結果Fig.7 The fitted curves of the Philip infiltration model

表4 Philip入滲模型擬合結果

滲率相比均非常低，甚至出現負值。原因與之前分析一致，是由于Philip入滲模型中時間指數設定為(-0.5)及較高的土壤初始入滲性能導致的。如表4所示，土壤入滲性能線源入流測量方法得到的不同坡度條件下的穩定入滲率雖然差別不明顯，但具有隨坡度增加而增加的趨勢。由于觀測過程中沒有受到雨滴打擊作用及地表結皮的影響，得到的結果可以用來準確分析坡度對入滲過程的影響。

3 結 論

土壤入滲性能線源入流測量方法在保證充分供水及保持土壤結構不被破壞的條件下，測量得到的土壤入滲率為土壤的最大入滲性能。本研究中利用的線源入流測量方法不受供水流量的限制，可以準確得到各因素對土壤入滲過程的影響作用：

(1)本研究結果表明,過于干燥或濕潤的土壤均不利于水分快速地滲入地表，中間含水量8.22%的土壤初始入滲率最高。過于干燥的土壤在入滲過程中由于快速濕潤可能會導致土壤團聚體的破壞，進而形成結皮、降低土壤入滲性能。濕土相對于干土而言，用于存儲入滲水量的孔隙較少，而且水力梯度較小。土壤初始含水量對穩定入滲率沒有明顯的影響。

(2)室內試驗也表明地表坡度的變化對土壤入滲性能沒有明顯的影響。

(3)應用Philip入滲模型模擬了這兩組室內試驗，模型較好地擬合了試驗數據并得到了一致的結論。

坡度和初始含水量對不同土壤類型的影響可能并不相同。更確切的土壤入滲性能影響因素的結論還需要進行更多的室內及野外試驗獲得。