鐵路信號聯鎖表計算機輔助設計主要算法與量化策略研究
李茂蛟
(中鐵工程設計咨詢集團有限公司,北京 100055)
1 概述
聯鎖表是車站信號設備聯鎖關系的信息說明圖表,以進路為單元,表達了進路與進路、進路與道岔及進路與信號機之間的制約關系。
鐵路信號設計人員完整地編制聯鎖表不僅是一項重要而繁瑣的設計工作,而且編制過程中很容易出現差漏,尤其是敵對信號及其敵對條件的差漏。利用計算機輔助設計是大幅提高聯鎖表編制效率的唯一途徑。但相關技術標準[1-3]及文獻[4]中僅從宏觀層面對聯鎖表編制的格式、內容以及敵對進路等概念進行了規定與定義,而基本進路與變更進路的選擇、變更按鈕的選擇等內容均具有較強的主觀性,以上因素都不利于計算機的自動處理。
本文對信號設備平面布置圖的結構化表達、聯鎖表進路的主要處理算法進行研究,以實現聯鎖表的計算機輔助設計。
2 信號設備平面布置信息化表達
結合圖論中“圖”的概念[5],將信號設備平面布置圖中信號機、絕緣節、道岔、軌道區段等抽象為含屬性的基本節點單元,則可將信號設備平面布置圖視為一張從左至右或從右至左的有向圖[6]。
為便于處理,對上述節點單元采用統一數據結構進行描述,具體的節點單元數據結構包括設備類型代碼、設備名稱及相關屬性等字段。
為精簡接口數據,結合聯鎖“進路”與圖論“路徑”的概念,按從左至右的順序將一條進路中的所有節點單元按序組成一束路徑數據,則全站信號設備平面布置圖的拓撲結構可由若干束路徑數據進行描述。
本文以符號v(x)表示設備x節點信息,以節點集合Rd={v(x1),v(x2),…,v(xn)}表示一條進路和路徑中順次經過的所有節點,其中,xi為進路或路徑中第i個設備名稱,n表示節點數量。在不涉及具體設備名稱的情況下,將v(xi)簡寫為vi。
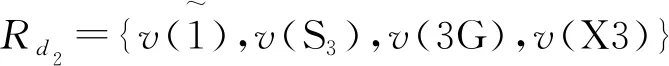
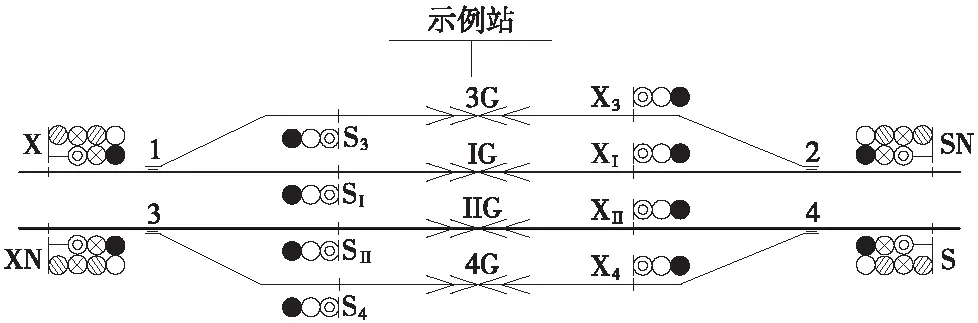
圖1 示例車站信號設備平面布置示意
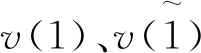
全站的進路搜索空間可表示為
Rd=[Rd1,Rd2,…,Rdn]T
(1)
其中,
Rdi={vi,1,vi,2,…,vi,m}
(2)
其中,m表示第i條路徑Rdi上所有的節點數量。
由此,可根據節點鄰接關系及具體屬性,采用圖論中相關路徑搜索算法進行進路搜索。對于圖1所示車站,全站若分咽喉表示,僅需8束路徑數據即可實現聯鎖表設計所需的全部信息的結構化存儲。
實現車站信號設備平面布置的結構化表達,可有以下兩種方式。
(1)人工編制結構化接口數據
設計人員根據車站實際的信號設備平面布置示意圖,按照上述路徑數據單元的表達方式,對車站的所有路徑逐條編制相應的路徑數據。該方法對平面圖繪制無特殊需求,且適合對既有紙質版平面布置圖進行結構化表達。
(2)計算機輔助設計
需在計算機輔助設計信號平面布置圖時,根據需要將相關信息附加到相應的設備圖元上,這樣,平面圖本身就包含了所需的信息,通過計算機程序根據需求即可提取所需的設備屬性及設備連接關系等信息。該方法一方面需要信號平面布置圖的繪制(本文僅討論AutoCAD制圖形式)遵循嚴格的規定,如需采用預先定義的圖塊單元來表達信號機、聯鎖道岔等信號設備,還需要為這些圖塊單元分別附加相應的屬性;另一方面,需要編制相應的AutoCAD插件,以提取相關屬性,從而根據上述路徑數據定義生成全站的路徑數據。
3 進路搜索算法與變更進路量化選擇策略
圖論中,路徑搜索算法有深度優先(DFS)[7]、廣度優先(BFS)[8]等多種搜索算法,對于本文采用的進路數據束結構,僅在道岔節點處有分支存在,本文采用DFS算法作為進路搜索核心算法,內存消耗較BFS算法小,且可在搜索過程中對搜索方向進行優化限制,如可限制直股優先或彎股優先。
3.1 進路基礎搜索算法
以Rt表示進路空間,以點v1表示進路搜索起始節點,以式(3) 表示搜索到節點vi時,已順序訪問的節點集合。
V(vi)={v1,v2,…,vi}
(3)
對于某節點vi(i>1),其父節點為vi-1,其子節點集合可表示為Vs(vi)={vi,j,j=0,1,2,…,k},其中,k表示子節點數量(k=0表示無子節點,即vi,0=?)。
不失一般性,以vc表示(任意)當前節點,則DFS(vc)遞歸過程如下。
a)令R=V(vc),判定是否構成合法的進路,若是,則將R存入Rt,并轉d),否則轉b);
b)搜索得vc子節點集合Vs(vc),若Vs(vc)=?,則轉d),否則轉c);
c)對Vs(vc)中每個有效節點vc,j,分別遞歸調用DFS(vcj);
d)令R=V(vc-1),返回上層遞歸狀態,若無上層遞歸,則結束;
由上述DFS算法過程可知,要實現進路搜索,需要設計合法進路的判定函數F(R),例如,對于式(3)中節點列表R=V(vi),若始端v1為出站信號機,終端vi為進站信號機,且二者方向相反,則可判定為合法的列車發車進路。
聯鎖系統中,進路需有明確的始端和終端,因此,進路搜索首先需提取進路始端設備,然后根據始端設備屬性,搜索所有可能的進路。對每一個進路始端節點,采用DFS算法,搜索以該節點為始端的所有合法進路,并將每條搜索出的進路存放于進路空間,最終得到全站所有的進路集合。
Rt=[R1,R2,…,Rn]T
(4)
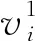
(5)
對于某進路R,根據式(5)所示的節點集合,可相應提取道岔、軌道區段等信息。以W(R)表示進路R內道岔及防護道岔(含道岔狀態)的集合,以T(R)表示進路R內的軌道區段集合。
3.2 基本進路量化選擇策略
在工程實際應用過程中,工程人員提出了不少基于經驗的確定基本進路與變更進路的規則與見解[9-10],但通常依賴于聯鎖表編制人員對于平面圖的直觀觀察與理解,其基本進路與變更進路的比選沒有量化指標,不便于計算機處理。
從進路之間相互關系出發,提出一種量化的進路比較算法,為每條進路賦予相應權值,從而根據權值大小確定基本進路與變更進路。
根據兩條進路所經過道岔的狀態與軌道區段的相互關系,將兩條進路Ra與Rb之間關系定義為以下三類。
(1)相互獨立。若W(Ra)與W(Rb)無相同道岔(同一道岔的定位與反位狀態視為相同道岔),且T(Ra)與T(Rb)無相同軌道區段,則Ra與Rb相互獨立。
(2)相互排斥。若W(Ra)與W(Rb)分別包含至少1組相同道岔的兩種狀態(定位/反位),則Ra與Rb相互排斥。
(3)相互重疊。若W(Ra)與W(Rb)不包含同一道岔的不同狀態(定位/反位),且T(Rb)包含至少1個相同軌道區段,則Ra與Rb相互重疊。
在不作特殊限制的情況下,相互獨立的進路能夠同時開放,列車經獨立進路相互之間不沖突;相互排斥的進路因道岔狀態沖突,是不可能同時開放的;相互重疊的進路能夠同時開放,但列車經相互重疊的進路可能發生沖撞。
對于進路空間Rt中的任意進路R,與之相互獨立的的進路數量Nd(R)越大,則說明受其影響的進路越少,因此,采用Nd(R)作為衡量進路影響的權值。
對于始端vs與終端ve均相同的m條進路構成的進路空間如式(6)所示
R(vs,ve)=[R1,R2,…,Rm]T
(6)
對式(6)所示進路空間按進路權值由大到小進行排序,得到
Rs(vs,ve)=[Rs,1,Rs,2,…,Rs,m]T
(7)
則標記Rs,1為基本進路,其余為變更進路。
如圖2所示為京張高鐵某車站右咽喉的信號設備平面布置示意,以SN至IG接車進路為例,存在兩條進路R1、R2,其順次經過的道岔狀態分別如式(8)、式(9)所示
W(R1)={2,8,16,20}
(8)
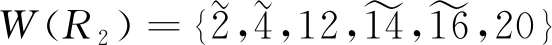
(9)
依據上述量化策略,計算兩條進路的權值分別為Nd(R1)=25,Nd(R2)=13,判定R1為基本進路,R2為變更進路。
由圖2可知,當R2進路排出時,由S、SC接車至IIG、4G、6G及由IIG、4G、6G向S、SC口發車的共12條進路無法排出,而當R1進路排出時,上述12條進路不受影響,上述12條進路即Nd(R1)與Nd(R2)的差值所在。另一方面,R1為直向進路,R2為八字進路,以上量化策略判定R1為基本進路,也與實際經驗相符。
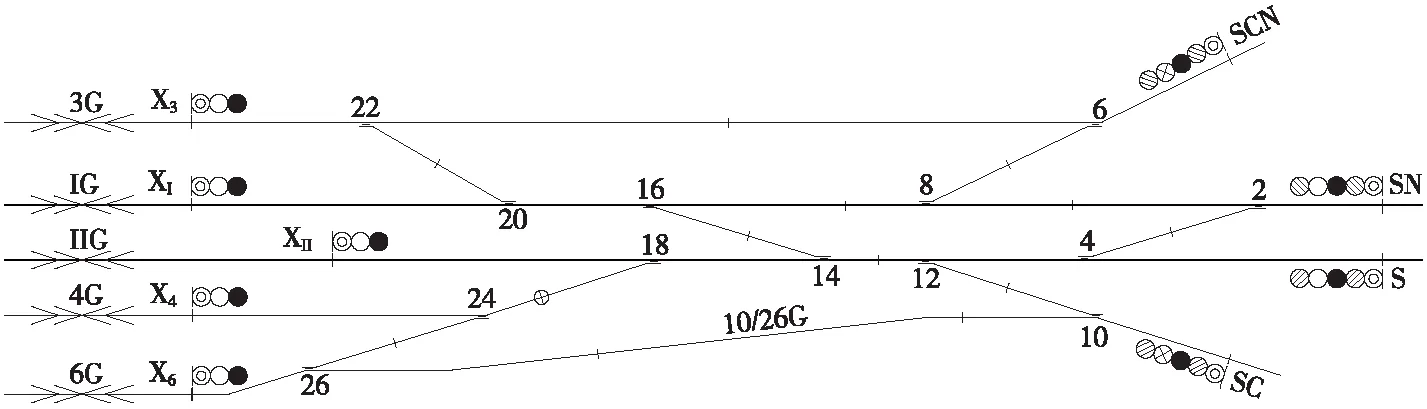
圖2 某站右咽喉信號設備平面布置示意
3.3 不合理進路判定策略
對始端vs與終端ve相同的兩條進路Ra與Rb,不失一般性地,假設Ra為基本進路,Rb為變更進路。若T(Rb)?T(Ra),即基本進路內的軌道區段均包含于變更進路內的軌道區段,則標記Rb進路不合理。一般來說,對于上述情形,如果變更進路Rb能辦理成功,則基本進路Ra亦能辦理成功,就沒必要辦理影響范圍大的變更進路。當然,實際應用時可僅對判定的不合理進路進行存疑標記,由設計人員參考相關部門意見后確定是否刪除以上不合理進路。
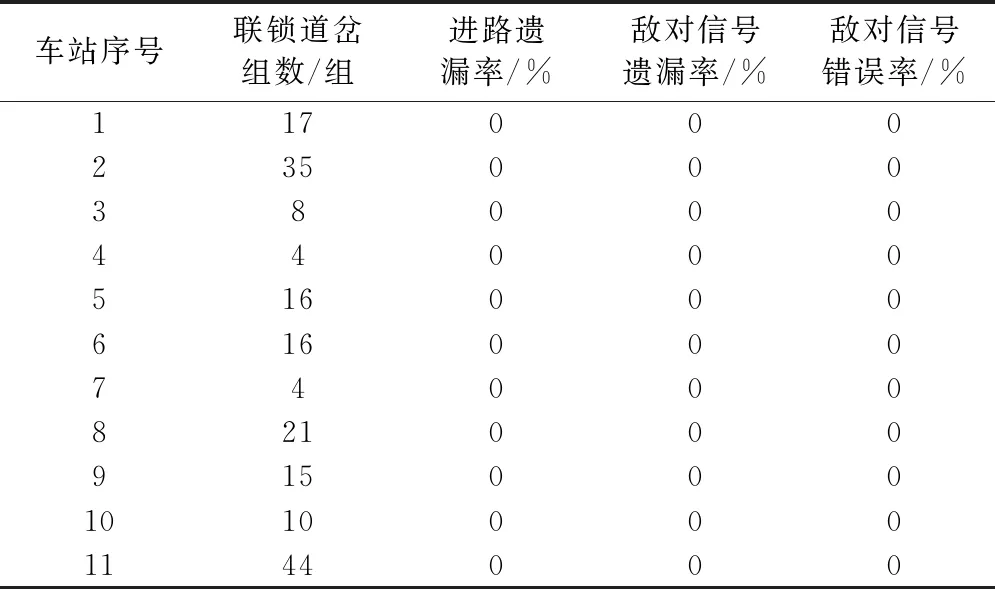
對于式(7)所示的進路集合,對于m>2(即具有兩條及以上的變更進路)的情況,需要依次對所有變更進路進行標記。即對于式(7)中已排序完畢的變更進路Rs,i(i>1),對任意j T(Rs,i)?T(Rs,j) (10) 若兩條(或兩條以上的)進路能同時辦理(即進路不相互排斥),但同時辦理以后有可能造成沖突的進路稱為敵對進路[11-12]。根據文獻[2]對敵對進路的劃分,將敵對進路歸納為以下兩種類型。 (1)重疊型敵對進路。根據本文對相互重疊進路的定義可知,與進路R相互重疊的進路可判定為進路R的敵對進路。 (2)侵限型敵對進路。防護進路的信號機設置在侵限軌道絕緣節處,不準許同時開通的進路。關于該進路,以圖3為例,對于D8至ⅡG的調車進路R(D8,XⅡ),由于D14處絕緣節侵限,為避免側面侵限沖突,禁止辦理以D14為終端的調車進路,該類進路為敵對進路。 圖3 某站信號平面布置圖局部示意 對于式(4)所示的進路空間Rt中的進路R,若存在某進路Rj≠R,使得Rj與相互重疊,則判定Rj為R敵對進路,并將添加至R的敵對進路空間Rc(R)中;否則繼續判定是否為R的侵限型敵對信號,判定流程如下: a)從T(R)提取絕緣節處為侵限的信號機集合S; b)若S為空,則返回,否則轉c); c)對S中的每一個信號機vs,從進路空間中搜索以vs為終端,且與相互獨立的進路子空間Rs,若Rs≠?,則Rs中各進路均為的敵對進路,將Rs添加至R的敵對進路空間Rc(R)中。 至此,即完成了R的敵對進路搜索,得到其敵對進路空間表示如式(11) Rc(R)=[R1,R2,…,Rk] (11) 對于進路Ra,其敵對進路的始端信號即為其敵對信號,其敵對類型與敵對進路類型一致。例如,若Rb為Ra的列車敵對進路,則Rb始端信號為Ra的敵對列車信號。 對式(11)所示的R的敵對進路空間,按照進路類型,提取其始端信號,構成無重復的始端信號集合如式(12) (12) c)初始化道岔集合Win=?和Wout=?,分別表示進路內和進路外道岔條件; d)對于每條進路Rx∈Rt(sj)且Rx∈Rc(R),取其道岔集合W(Rx)中第一個包含于W(R)中的道岔狀態wx,in,若wx,in?Win,則將wx,in添加至Win; e)對于每條進路Rx∈Rt(sj)且Rx∈Rc(R),取W(Rx)中最后一個不包含在W(R)中的道岔狀態wx,out,若wx,out?Wout,則將wx,out添加至Wout; 最終,若Win不為空,則Win中的道岔狀態即為進路內敵對條件;Wout不應為空(否則應為無條件敵對),Wout中的道岔即為進路外敵對條件,二者選其一作為敵對條件即可。 圖4 某車站過渡階段平面布置局部示意 本文主要討論關鍵道岔提取算法和變更按鈕選擇算法。前者具有確定性,不受編制人員主觀影響,但其判定邏輯和算法實現并不直觀,值得討論;后者往往具有較大的主觀性,在計算機處理時,需確定其量化比較策略。 文獻[13]規定,當有兩種以上運行方式時,為區別開通的進路,需填寫關鍵對向道岔的位置(定位/反位)。將從算法層面探討關鍵道岔的搜索方法。 對于任意兩條始端vs與終端ve相同的進路,二者由始端開始,必然分別經由某個道岔wf的不同位置產生分支,方能形成不同進路;之后必然再分別經由某個道岔wh的不同位置重新匯聚,方能到達同一終端。這里,產生分支的道岔wf,以下稱為二分道岔,其定位與反位即為兩條進路的關鍵道岔位置。例如,假設基本進路R0(vs,ve)和變更進路的道岔狀態集分別如式(13)和式(14)所示 W0={wf,w0,1,w0,2,…,wh,…,w0,k} (13) (14) 則顯見,兩條進路分別經由道岔wf的定位和反位產生分支,經由道岔wh的定位和反位最終匯聚。因此,道岔wf的定位與反位即為兩條進路的關鍵道岔位置。 在排列變更進路時,為區分于基本進路及其他變更進路,需在始端按鈕、終端按鈕之間設置變更按鈕[14]。對于進路R,以Sg(R)表示進路內始端按鈕和終端按鈕之間的可用作變更按鈕的調車信號集。 若變更進路Rb對應的Sg(Rb)中有可用作變更按鈕的調車信號,則可選擇合適的調車信號按鈕作為變更按鈕;否則,需在進路中合適的區段單獨設置變更按鈕。本文對以下問題的量化解決方案進行討論。 (1)進路中有多個調車信號可設為變更按鈕時,如何選擇。 (2)需單獨設置變更按鈕時,設置于進路中哪個區段。 變更按鈕的作用在于與始端按鈕、終端按鈕按照順序唯一確定一條進路,因此,在保證始端按鈕、變更按鈕、終端按鈕的排列不重復的前提下,變更按鈕是可復用的。以變更按鈕最大化復用(即變更按鈕或用于變更按鈕的調車按鈕數量最小化)為目標,設計變更按鈕的最優化選擇策略如下。 首先,為搜索空間Rd的軌道區段及調車,信號節點vx按以下方式賦予權值。 令初始權值We(vx)=0,對進路空間Rt中的每條變更進路R,若vx為調車信號,且vx∈Sg(R),則令權值We(vx)加1;若vx為軌道區段,且vx∈T(R),則令權值We(vx)加1。 然后,對于以上(1)、(2)所述問題,選擇權值較大的一項即可。 以京張高鐵全線11個車站(不含中繼站、線路所及既有改造站)為例,對上述算法與策略進行驗證。通過對本文算法生成的各站聯鎖表采用兩級人工復查的方式進行檢驗,結果如表1所示。 表1 本文算法及量化策略指標算法指標檢算 其中,進路遺漏率為未搜索出的合法進路數量與總進路數量之比;敵對遺漏率為敵對信號有遺漏的進路數量與總進路數量之比;敵對錯誤率為包含錯誤敵對信號(含敵對條件錯誤)的進路數量與總進路數量之比。 由表1可見,本文提出的算法、策略能夠完整地搜索全站進路以及敵對信號,準確率較高。 以上測試均由設計人員根據信號設備平面布置示意圖編制結構化的接口數據實現。設計效率可通過完善信號平面布置圖的信息化輔助設計軟件進一步提高。4 敵對信號搜索及敵對條件計算
4.1 敵對進路搜索

4.2 敵對信號搜索
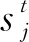

5 其他算法與量化策略
5.1 關鍵道岔搜索算法
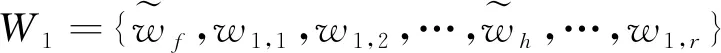
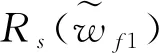
5.2 變更按鈕選擇的量化策略
6 結論與展望