關(guān)于對(duì)算術(shù)基本定理證明的再認(rèn)識(shí)

(喀什大學(xué)數(shù)學(xué)與統(tǒng)計(jì)學(xué)院，新疆喀什 844000)

算術(shù)基本定理或唯一因子分解定理指出：每個(gè)大于1 的整數(shù)均可以唯一地表示成一些素?cái)?shù)冪的乘積.下文均稱(chēng)唯一因子分解定理.這個(gè)重要定理有多種證明方法和應(yīng)用[1-3].在初等數(shù)論中，用于研究Riemann-zeta 函數(shù)就是其最重要的應(yīng)用.

設(shè)s∈C 且Re s＞1，則Riemann-zeta 函數(shù)由

所定義.當(dāng)你第一次看到這個(gè)函數(shù)時(shí)，根本不清楚為什么它值得研究，或者為什么凱萊數(shù)學(xué)研究所提供100 萬(wàn)美元用于資助研究其零點(diǎn)的位置問(wèn)題！事實(shí)證明，Riemann-zeta 函數(shù)是數(shù)論中最重要的函數(shù)之一.由唯一因子分解定理，可將 Riemann-zeta 函數(shù)重新改寫(xiě)為乘積形式，即若Re s＞1，則

其中P 是素?cái)?shù)的集合[4].Riemann-zeta 函數(shù)的這種關(guān)系是許多數(shù)論問(wèn)題研究的出發(fā)點(diǎn).雖然整數(shù)可表為素?cái)?shù)的乘積，但是要準(zhǔn)確掌握素?cái)?shù)的分布和性質(zhì)卻是十分困難的[5].相反，整數(shù)就很好理解.比如，素?cái)?shù)17483 之后的下一個(gè)素?cái)?shù)是什么?（是17489）并不是顯而易見(jiàn)的；但是，我們卻很容易找到17483 之后的下一個(gè)整數(shù)！然而，由于和與積是等價(jià)的，所以我們可將整數(shù)的信息轉(zhuǎn)換為素?cái)?shù)的信息，而解決問(wèn)題的關(guān)鍵在于證明唯一因子分解定理.

本文的目的不只是為了討論唯一因子分解定理或類(lèi)似結(jié)果的證明，而是要強(qiáng)調(diào)在試圖證明某個(gè)命題時(shí)，如何巧妙地應(yīng)用假設(shè)所蘊(yùn)含的事實(shí).

定理1（唯一因子分解定理）每個(gè)大于1 的正整數(shù)均可以唯一地表示成一些素?cái)?shù)冪的乘積.

分析：證明要分兩個(gè)步驟.

（1）證明每個(gè)整數(shù)至少可寫(xiě)為兩種素?cái)?shù)冪的乘積，即存在性；

（2）證明這兩種分解（需重新排列因子順序）是相同的，即唯一性.

眾所周知，整數(shù)n≥2 稱(chēng)為素?cái)?shù)，如果它只能被1 和自身整除，1 稱(chēng)為單位.非素?cái)?shù)的其它正整數(shù)稱(chēng)為合數(shù).這里要注意，1是單位而非素?cái)?shù)，否則唯一因子分解定理不 成立.例 如，6=1·2·3=12020·2·3.這就是為什么在素?cái)?shù)定義中要求整數(shù)必須大于等于2 的原因.

第二數(shù)學(xué)歸納法是證明唯一因子分解定理存在性的一種有效方法，它與第一數(shù)學(xué)歸納法類(lèi)似.兩者都要求證明命題P（n）n 對(duì)n=1(或另一個(gè)固定的自然數(shù)r，這取決于命題的起始計(jì)數(shù)）正確.在第一數(shù)學(xué)歸納法中，需證明：若P（n）正確，則P（n+1）也正確，并得出P（n）對(duì)所有n≥r 正確的結(jié)論；在第二數(shù)學(xué)歸納法中，需證明：若P（k）對(duì)所有k≤n 正確，則P （n+1）也正確，并得出P（n）對(duì)所有n≥r 正確的結(jié)論.

證明：（1）存在性.顯然，2 是素?cái)?shù)冪的乘積，因?yàn)? 本身就是素?cái)?shù).假設(shè)所有正整數(shù)k（2≤k≤n）均可寫(xiě)成素?cái)?shù)冪的乘積.現(xiàn)在，考慮正整數(shù)n+1.它或者是素?cái)?shù)（證明完成），或者可被某個(gè)素?cái)?shù)p 整除，即p|（n+1）(因?yàn)槿鬾+1 不是素?cái)?shù)，則它為合數(shù).于是，n+1 可分解成兩個(gè)小于n 的正整數(shù)乘積.如此下去，便可找到素?cái)?shù)p.）.令n+1=pm，其中m＜n，由假設(shè)，m 可表為素?cái)?shù)冪的乘積.因此，由第二數(shù)學(xué)歸納法，存在性得證.

為了證明唯一性，先給出下面引理.

引理1給定素?cái)?shù)p 和整數(shù)a，b.若p|ab，則p|a 或p|b.

我們把引理1 的證明放到最后.這里需要強(qiáng)調(diào)的是，引理1 是證明定理1 唯一性的關(guān)鍵，即一旦證明了引理1，唯一性證明的剩余部分隨即可得.

（2）唯一性.用反證法.若因子分解的唯一性不成立，則必有一個(gè)最小正整數(shù)，設(shè)為n，其因子分解的唯一性不成立.因此，不妨設(shè)n 有兩個(gè)不同的因子分解式，即

現(xiàn)在，考察n／pk＜n.顯然，它只有唯一的因子分解式.否則，將與n 是具有兩個(gè)不同因子分解式的最小整數(shù)的假設(shè)矛盾.

定理1 證畢.

由此可見(jiàn)，整數(shù)環(huán)上因子分解的唯一性，關(guān)鍵是要證明引理1 正確.這一點(diǎn)盡管看起來(lái)很簡(jiǎn)單，但必須得到嚴(yán)格證明，尤其是在某些環(huán)上，歸納法失效的情況下更是如此! 例如，考慮高斯環(huán)

的函數(shù)構(gòu)成的環(huán)，其中ai，bi∈R 且n∈N .在這里，由于

所以，三角多項(xiàng)式環(huán)上因子分解的唯一性不成立[6]，并且sinx 既不整除1-cosx，也不整除1+cosx.

關(guān)于引理1 的證明，許多教材使用的標(biāo)準(zhǔn)方法都是Euclidean 算法（帶余除法）或貝祖等式[3].

所謂貝祖等式，即下面的定理.

定理2（貝祖等式）給定a，b∈Z，?x，y∈Z，使得xa+yb=gcd （a，b）(其中g(shù)cd （a，b）是a 和b 的最大公因數(shù)），即同時(shí)整除a 和b 的最大整數(shù).

證明 只證明gcd （a，b）=1 的情況，當(dāng)gcd（a，b）=d＞1 的情況類(lèi)似可證.在這里，給出x 和y存在性的一個(gè)新的非構(gòu)造性證明.設(shè)

為了完成證明，必須推出k=1.首先，證明k整除A 中的每一個(gè)數(shù).假設(shè)情況并非如此，即k 不能整除A 中的每一個(gè)數(shù).由于這個(gè)數(shù)在A 中，所以必有整數(shù)x1和y1，使得它等于x1a +y1b.設(shè)n 是滿(mǎn)足nk＜x1a +y1b＜（n+1）k 的最大自然數(shù).因?yàn)椋覀円恢痹谠黾觡 的倍數(shù)，直到它首次超過(guò)x1a+y1b為止.而且，必須有

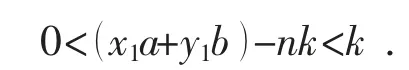
不妨設(shè)在第q 步時(shí)，中間表達(dá)式等于0，于是x1a+y1b=qk，即k| （x1a+y1b）.這與x1a+y1b 是A 中不能被最小數(shù)k 整除的假設(shè)矛盾.類(lèi)似地，可以證明中間表達(dá)式也不能等于k.

因?yàn)閗=x0a+y0b，所以有

由于這是一個(gè)正數(shù)且形如xa+yb，因此它必屬于A.此外，它嚴(yán)格小于k，這與k 是A 的最小數(shù)矛盾.因此，A 中存在一個(gè)不能被k 整除的數(shù)的假設(shè)錯(cuò)誤，從而A 中的所有數(shù)都可被k 整除.

特別地，若取x=1，y=0，則a∈A；同時(shí)，若x=0，y=1，則b∈A.因此，k|a 且k|b .因?yàn)間cd（a，b）=1，即a 和b 沒(méi)有公因數(shù)，所以必有k=1.因此，適當(dāng)選取x0和y0，可得1=x0a+y0b.

定理2 證畢.

貝祖等式對(duì)引理1 的證明至關(guān)重要.事實(shí)上，假設(shè)p|ab，但.將貝祖等式應(yīng)用于p 和a 上.注意到，gcd（p，a）=1.因此，?x，y∈￠，使得xp+ya=1.兩邊乘以b，可得xpb+yab=b.因p|p且p|ab，故p|（xpb+yab），即p|b.矛盾！可見(jiàn)，貝祖等式起到了“橋”的作用.

注1：貝祖等式的逆命題不成立！

在使用貝祖等式時(shí)，認(rèn)為沒(méi)有k|gcd（a，b），就能有k|a 和k|b 是非常錯(cuò)誤的.幸運(yùn)地是，在因子分解唯一環(huán)中，證明k|gcd（a，b）卻相當(dāng)簡(jiǎn)單!

引理2在因子分解唯一環(huán)Z 中，給定a，b∈Z 和k∈N .若k|a 且k|b，則k|gcd（a，b）.

證明 由唯一因子分解定理，可設(shè)a 和b 可以分別表示為

其中ri，si∈N （i=1，…，l）.令可以證明d=gcd （a，b），此處省略.

若k|a 且k|b，則k 可寫(xiě)為

注意到，由k|a，可得ui≤ri（i=1，…，l）.同樣，由k|b，可得ui≤si（i=1，…，l）.于是，有ui≤min(ri，si)=ti（i=1，…，l）.因此，可得k|d.

引理2 證畢.

注2：從引理2 的證明過(guò)程可以發(fā)現(xiàn)唯一因子分解定理的另一個(gè)應(yīng)用，即尋找兩個(gè)整數(shù)的最大公因數(shù).

現(xiàn)在，回到證明引理1 的問(wèn)題上.順便說(shuō)一句，為了證明唯一因子分解定理，只需引理1 就夠了，而不需要有比貝祖等式更強(qiáng)的命題了.下面，給出引理1 的強(qiáng)調(diào)兩種不同觀點(diǎn)的證明.這兩種證明都用到了Euclidean 算法（帶余除法），即設(shè)a，p∈N.若a＞p 且則?n∈N 和r∈{1，…，p-1}，使得a=np+r.值得注意的是，引理1 的兩種證明都未使用有關(guān)最大公因數(shù)（在Euclidean算法的標(biāo)準(zhǔn)證明中用到）的任何結(jié)果，但卻用到了最小數(shù)原理，即具有某種性質(zhì)的任何非空正整數(shù)集必有一個(gè)最小數(shù).

引理1證法一：

由前面的討論已知，若p為素?cái)?shù)且gcd（a，p）=1，則?x，y∈Z，使得xp+ya=1.然后，兩邊同乘以b，得到xpb+yab=b.若假設(shè)則由已知條件和整除的性質(zhì)可知p|（xpb+yab），從而p|b.

引理1證法二：

（2）假設(shè)這樣的素?cái)?shù)p 存在，a 和b 使得乘積ab 在所有整數(shù)乘積中最小.若分解a 和b 之后，有幾個(gè)乘積都得到相同的最小乘積，為明確起見(jiàn)，則取包含a 的那個(gè)最小乘積.

（3）證明a，b＜p.顯然，a，b≠p.假設(shè)a＞p（b＞p時(shí)同樣）.由帶余除法定理，a 可寫(xiě)為a=np+r 且0＜r＜p.于是，ab=（np+r）b=nbp+rb.因p|ab，故p|rb.然而，rb＜ab，這與乘積ab 的最小性矛盾.因此，有a，b＜p.

（4）由于所有整數(shù)都有素因數(shù)分解，所以可將ab 寫(xiě)為ab=qa，1…qa，l·qb，l…qb，m.根據(jù)p|ab 的假設(shè)，可將ab 改寫(xiě)為ab=np （n∈N） .因此，有np=qa，1…qa，l·qb，l…qb，m.

由假設(shè)（1），存在一個(gè)乘積，使得p 為整除該乘積，但不整除兩個(gè)因數(shù)的最小素?cái)?shù).由于a 的因數(shù)最多只有a＜p 個(gè)（b 的因數(shù)最多只有b＜p個(gè)），所以由歸納法可得，每個(gè)因數(shù)qa，i和qb，j，或者整除n，或者整除p.因p 是素?cái)?shù)，故qa，1，…qb，m均不能整除p，又因?yàn)橐鸭僭O(shè)如果qa，1|p，那么就有qa，1=p .從而，p|a.矛盾！

（5）由于每個(gè)因數(shù)qa，1，…，qb，m均整除n，所以當(dāng)ab=np 時(shí)，可得這是不可能的，因?yàn)閜≥2.

綜上可知，不可能存在這樣一個(gè)最小素?cái)?shù)，它整除乘積，但不整除乘積中的任何一個(gè)因數(shù).

引理1 證畢.

素?cái)?shù)整除一個(gè)乘積就必須整除其中的某個(gè)因數(shù).這個(gè)結(jié)論是證明唯一因子分解定理的關(guān)鍵所在.本文實(shí)現(xiàn)了兩個(gè)目的.一是強(qiáng)調(diào)了那些看似平常的陳述必須嚴(yán)格證明.因?yàn)閷W(xué)生很容易被符號(hào)所誤導(dǎo).例如，兩個(gè)整數(shù)的最大公因數(shù)實(shí)際上就是它們公因數(shù)中最大的那個(gè).但在具體問(wèn)題的證明中，學(xué)生往往忽視對(duì)“公共”這一點(diǎn)的證明；二是要準(zhǔn)確、全面地把握住結(jié)論的內(nèi)涵，具體地說(shuō)，就是要證明某個(gè)結(jié)論成立，究竟需要多少論據(jù)來(lái)支撐這些邏輯推理.