夯實基礎提高小學生自信心
林鳳嬌

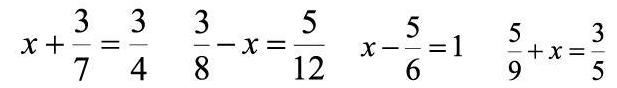
隨著教學的改革,對學生的考查也在不斷地改革。為了考察學生的素質,考試的題目也越來越靈活,好多題跳出平常練習內容。為了提高考試的分數,學生在不停地刷題。在刷題的過程中,很多時候會越走越遠,忘了本,忘了基礎的重要性。基礎沒夯實,對于一些靈活的題是很難把握與解答的。當刷題多了,錯題多了,學生就會對自己越來越懷疑,越來越沒信心,認為自己沒有學習的天賦,怎么學都學不好。所以在學習過程中不要急著做難題,首先把基礎弄懂,弄明白。因為基礎是最簡單的,也是最容易弄懂的,最容易獲得成功感的題,最能提高自信心的題。
一、為什么要提高自信心
愛爾蘭著名的戲劇家蕭伯納曾經說過:“有信心的人,可以化渺小為偉大,化平庸為神奇。”這道出自信心的神奇效應。在學習的過程中,如果充滿自信心,會越學越好,越好就越有自信心。
學習也是培養自信心的過程,但也可能是打擊自信心的過程。當作業里錯的比對的多時,每個學生的心理都會陰沉下來,如果經常這樣,自信心就會消磨掉。當失去自信心時,學習就會越來越糟糕。
當作業里的紅紅√多于紅紅的×時,學生的信心就會增強,認為自己的腦袋瓜子還是挺聰明的,對教師上課的內容就感興趣;當學生在課堂上回答正確老師提出的問題時,更覺得自己了不起了。因此,基礎的知識掌握好后,就會不滿足于現狀,渴望能做難一點的題,會主動去探討更深更難的題,慢慢地靈活的題也學會了,成績也提高了。因此,為了提高學生的自信心,必須讓學生從基礎題做起,基礎題是最簡單易學的題,學生掌握了,就有了自信,就有了學習的欲望。
二、如何打好基礎
(一)講解要簡單易懂
數學的知識雖然來源于生活,但它又高于生活,因為它是從實際生活中抽象出來的。老師在講解的時候需要把它還原,用實際的情境,引導學生分析理解。
在學圓柱的表面積時有這樣一道題:一臺壓路機的前輪是圓柱形,輪寬2m,直徑1.2m。當前輪向前滾動一周,壓過的路的面積是多少平方米?不是每個學生都那么幸運地能在現實生活中看過,壓路機是怎么壓路的。沒有目睹過得學生是很難理解的,壓路機的前輪是什么形狀的,前輪滾動時,留下的軌跡是圓柱的哪個面,這需要老師的直觀演示。取一個卷紙(廁所常用)當做前輪,把它放在黑板上,向學生演示滾動一周是怎么樣的,(滾動后,黑板就會留著卷紙滾過的痕跡:長長的紙)學生看了演示后立刻明白,輪子滾動一周所壓過的地方就是一個長方形,這個長方形就是圓柱的側面積。使學生理解壓路機前輪滾動一周就是求圓柱的側面積。
著名教育學家夸美紐斯說過:“知識的開端永遠是從感官得來的。” 實物演示擺脫了枯燥的講解,吸引了學生的眼球,提高了學生的學習興趣,也把知識變得簡單易有趣。
學生喜歡了,就會產生想學的欲望,那么基礎就打得牢固了。
(二)練習要注重基礎
數學的題目是靈活多變的,同樣一個問題,有好多種問法,稍微改變一下條件,又變成另外一道題。接受能力慢的學生會最怕這樣的變化,前面的題目還沒有搞明白,下一道題就來了。因此,基礎題必須要理解好、掌握好。
圓柱的體積練習題的種類繁多,但所有的變化都離不開基礎公式。當學生理解了圓柱的體積公式后,就做下面的鞏固練習,所以在推導完圓柱的體積公式后,就經常讓學生練熟下面的題:
①一個圓柱體的底面積是75平方厘米,高90厘米,它的體積是多少?
②一個圓柱的底面直徑是60平方厘米,高45厘米,它的體積是多少?
③一個圓柱的底面半徑是25平方厘米,高40厘米,它的體積是多少?
④一個圓柱的底面周長是6.28平方厘米,高40厘米,它的體積是多少?
后面3道題是在第1道題變化過來的,但這4道題又是其他題目變化的基礎。如:
⑤一個圓柱形糧囤,從里面量得底面半徑是1.5m,高2m.如果每立方米玉米約重750kg,這個糧囤能裝多少噸玉米?
有了第③小題的基礎,學生解決這道題主要掌握一個知識點就行了:每立方米的重量×幾立方米=總重量。
再變化是:
⑥一個圓柱形糧囤,從里面量得底面半徑是1.5m,高2m.如果每立方米玉米約重750kg,如果要用載重3噸的車來運,要運多少次?
有了第⑤小題的基礎,學生解決這道題主要掌握一個知識點就行了:總重量÷每輛車的載重=運的次數。
這道題本來是3個知識點,如果不分散處理,一些接受能力弱的學生是無所適從的。
新課程理念強調“小學數學課程必須突出體現基礎性”基礎題是一切發展題的墊腳石,上面的例子顯示出題目是怎樣一步步變過來的,學生也一點點地掌握,慢慢地學,進而掌握。此外,難理解的知識點要經常反復練習,在練習中理解和掌握。
(三)測驗要及時反饋
基礎知識打得是否牢固要通過測驗來檢查,最快的測驗是課堂小測。由于是每節課都要進行小測,所以測題不要多,看測試內容而定,如果簡單題,可以多些,復雜的題,難度大的題題量可以少些,占用的時間是5分鐘左右。如:
同分母分數加減法比較簡單易算,占用的時間不多,可以多出2題,以便更清晰地看出學生對知識掌握程度。
加減法的方程題只有4種類型,它的計算步驟比較多,每種題出一道就可以看出學生是否掌握解題方法:
比例尺應用題只要掌握三道公式就可以解決好多問題,所以它的基礎題是求實際距離、圖上距離、比例尺的應用題。可以直接給出條件讓學生算,因為要考察的是公式的熟練掌握與應用,出的數字要簡單易算。
①蘇明家到陳玉家是120km,畫在地圖上的距離是2.4cm,這幅地圖的比例尺是多少?
②蘇明家到陳玉家是80m,用1:2000的比例尺畫在地圖上,請問可以畫多少厘米?
③蘇明家到陳玉家在比例尺是1:5000的地圖上量得的距離是15cm,實際上這兩家的距離是多少?
萬丈高樓從地起,基礎是一切上層建筑的根本,基礎越牢固,樓就建得越高。基礎扎實了,思維才得以開闊,人就會越學越聰明,越學越有信心。

