核心素養引領下的經典問題解答新思路探究
——由一道初三上學期期中考試題說起

江蘇省蘇州市相城區東橋中學 凌 健

有一年初三數學第一學期期中試卷第28題的第（3）小題，筆者任教的兩個班得分率特別低，得滿分的寥寥無幾。為此筆者對這個題目進行了深入的研究，試圖找出癥結所在，通過思考問題的本質，找到了其中的共性和特性。本文給出對該題的一題多解，解后反思及教學反思，期待與同行交流。

一、試題呈現

如圖1，在平面直角坐標系中，點A的坐標是（8，0），點的坐標是（0，6），點P從點O開始沿軸向點以1cm/s的速度移動，點Q從點B開始沿y軸向點以相同的速度移動，若P、Q同時出發，移動時間為t（s）（0＜t＜6）。

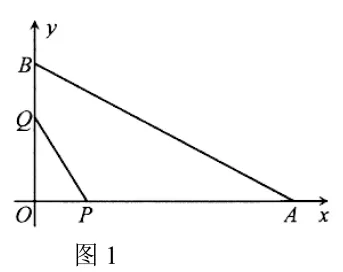
圖1

（1）當PQ//AB時，求t的值；

（2）是否存在這樣t的值，使得線段PQ將△AOB的面積分成1:5的兩部分。若存在，求出t的值；若不存在，請說明理由；

（3）當t=2時，試判斷此時△POQ的外接圓與直線AB的位置關系，并說明理由。

二、解法展示

問題（3）要判斷當t=2時△POQ的外接圓與直線AB的位置關系，先要計算出d和r，再通過d和r比較大小進行判斷。由題意可知0P=2，OQ=4，△POQ是直角三角形，所以外接圓圓心在PQ中點M（1，2）處以只要求出MH（如圖2）的長度即可。

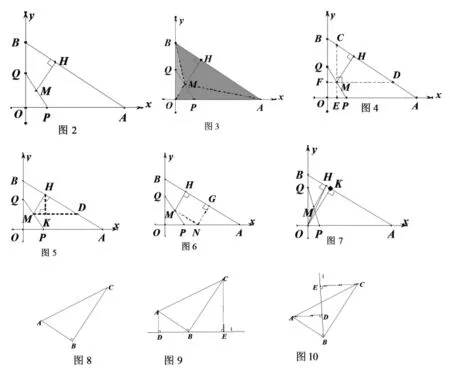
圖2

解法1：利用等積法求線段MH的長度。

如圖 3，連接 MB、MA、MO。

因為 S△AOB=S△ABM+S△AOM+S△BOM，

S△AOB=24，S△BOM=3，S△AOM=8，所以 S△ABM=13.

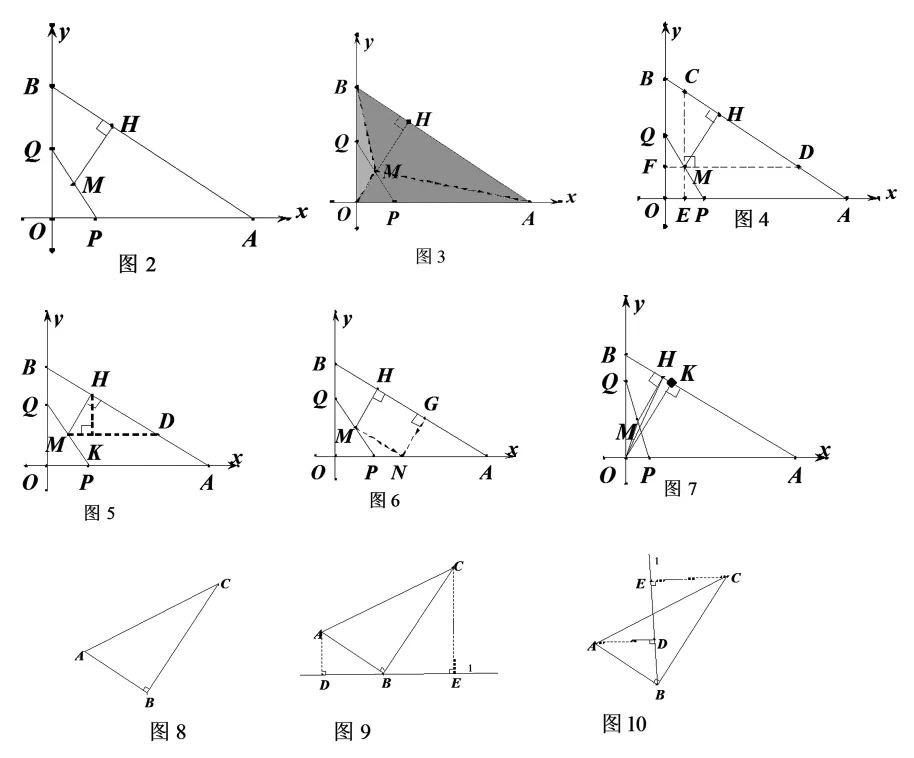
圖3

解法2：構造相似模型求線段MH的長度

如圖4，過點M作ME⊥x軸于E，交AB于點C；過點M作MF⊥y軸于F，交AB于點D。

圖4

解法3：通過增量巧設簡化相似計算過程

如圖5，過點M作MD//x軸，交AB于點D；過點H作HK⊥DM于K。由題意可知，△MHK∽△BAO，可得MK：HK：MH=3:4:5，設 MK=3a，HK=4a，由 M（1，2）可得 H（1+3a，2+4a）由直線 AB

圖5

解法4：將MH轉化為特殊位置的垂線段NG

如圖6，過點 M作MN//AB，交x軸于點N；過點N作NG⊥AB于點G由直線AB解析式為AB，可將直線MN的解析式設為

圖6

解法5：通過“折直垂”巧妙轉化為最值問題

如圖7，過點M作MH⊥AB于點H，連接OH；過點O作OK⊥AB于點K，若以PQ為直徑的圓M與AB相切，則OM=MH=2，由于OM+MH≥OH≥OK，而OK=4.8＞OM+MH=2矛盾，所以d＞r，直線AB與圓相離。

圖7

當然，本題也可以用垂直的兩條直線斜率互為負倒數來解決，但由于超出了初中數學課程標準的要求，這里就不予討論了。

三、命題思考

1.經典問題，推陳出新，有的放矢，考查素養。

這道期中壓軸題以一次函數為背景，推陳出新，圖形簡潔，題干簡約易懂。第3小題集中考查了判斷直線與圓的位置關系，直角三角形外接圓的圓心確定方法，點到直線距離的精準作圖能力，垂直條件的轉化方法，運用基本思想和方法構造基本圖形計算垂線段長度等數學的核心概念和內容。在解題的過程中對學生的解題能力和數學素養都提出了很高的要求。

2.一題多解，發散思維，殊途同歸，考查能力。

本考題第3小題的設問簡潔，言簡意賅，學生思路清晰，解法自然生成。判斷直線與圓的位置關系，關鍵要找到圓的半徑r和圓心到直線的距離d。由于圖中沒有d，故第一步就是作d。接著要轉化垂直這個條件，方法很多，起到鍛煉學生思維的作用。比較常用的有等積轉化，構造K型相似等等，針對本題定三角形定直線也可以找到最值等特殊的解法。解法的起點很低，但解題過程中卻困難重重，每一種方法都對解題的抽象思維和邏輯推理要求很高，試題的區分度明顯。

鬼斧神工的解法，無不以學生分析問題，解決問題的能力為基礎，對學生能力的要求尤為突出。這些都給教師平時的教學提出了要求，指明了方向。

四、教學思考

1.要重視對學生數學核心素養的發展。

王尚志教授指出，數學核心素養包含數學抽象、邏輯推理、數學建模、數學運算、直觀想象、數據分析六個方面。數學的學習就是從已知條件出發，對問題進行數學抽象，通過邏輯推理，數學建模，數學運算等等解決問題。在日常的教學過程中，要重視對學生數學核心素養的發展，一切以學生的發展為中心，以生為本，培養能力。在學習的過程中，要幫助學生養成良好的學習習慣。對于數學問題，要幫助學生建立一套研究問題的方法，創造足夠的時間和空間，讓學生自主探究和創造。

2.要重視對學生“四基”“四能”的培養。

教師在教學的過程中要高度重視基礎知識、基本技能、基本思想方法和基本活動經驗等內容。在學習的過程中深化對基礎知識的理解并逐步遷移，讓學生經歷知識產生、發展的全過程，培養學生發現問題，提出問題，分析問題和解決問題的能力。試卷中的試題，其本質考查的是學生對書本上的基本概念和基礎知識的掌握程度和靈活應用能力，因此不管題目的形式如何改變，但萬變不離其宗。要引導學生注意基礎知識之間的內在聯系和對一些問題通性通法的熟練掌握，重視基本技能和數學思維方法的應用。本題我任教的兩個班級得分很低充分暴露出學生基礎不扎實和分析問題、解決問題能力不足的短板。

3.要重視對經典問題的回顧和反思。

這道試題給了我們很多的教學啟示，比如，要重視對經典問題的回顧和反思。平時常考的一些問題，要讓學生自己歸納總結。類似的問題，要讓學生總結題目的條件會有哪幾種形式，題目的問題有哪些常見的提問角度，解答的方法具體有哪些，最優化的解答如何選擇等等。培養學生自己悟數學，將知識點連成線，線再連成片織成一張網，在不斷的回顧和反思的過程中提升能力，發展素養。

4.要重視基本圖形的研究。

所謂基本圖形就是將在“圖形與幾何”領域的學習過程中具有一定典型性的概念、公式、定理、例題、習題中反復出現、經常用到的對應圖形，是結論化的圖形，是圖形化的公式。借助基本圖形，可以使得復雜問題簡單化，有利于提高學生的幾何直觀能力。

例如，對于垂直條件的轉化，轉化為K型相似是一種方法。研究的過程，教師可以引導學生從圖形本身開始研究，慢慢進行變式和變形，最后實現升華，讓學生根據圖形特征創造性的自主建構基本圖形，最后通過總結條件和構圖步驟等將知識點內化，積累數學基本活動經驗。在遇到例如圖8的垂直問題時，學生就會創造性的建立圖9或圖10，利用相似轉化垂直條件了。

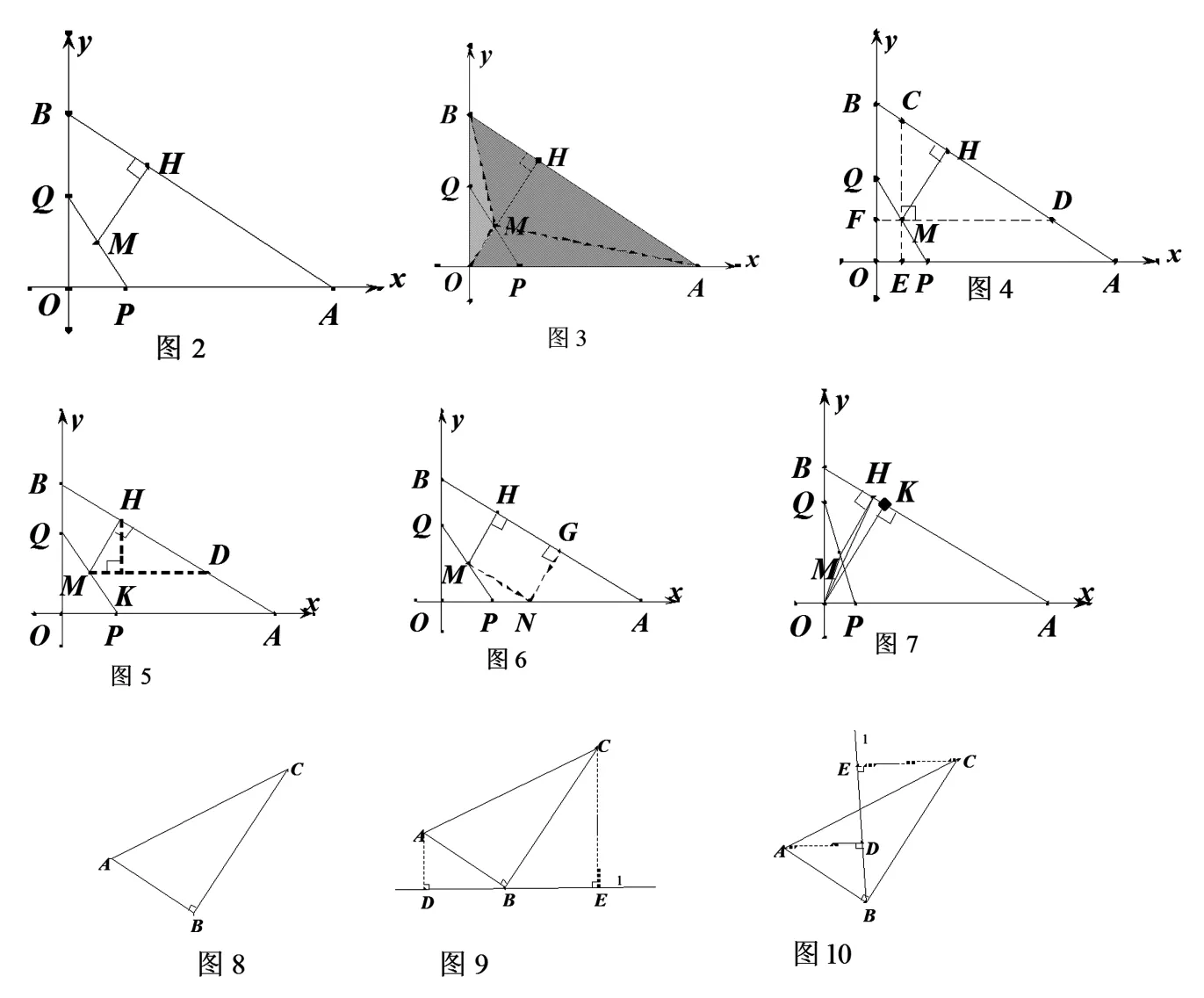
圖8

圖9

圖10

在平時的教學中要重視引導學生分析條件，聯想基本圖形。有了基本圖形的積累，學生能夠在它們的指引下主動探索，創造性的添加輔助線，發現解題思路，并解決問題。對基本圖形的研究，不僅僅是為發現了多少新的規律和結論，更為重要的是掌握圖形研究的步驟、方式方法和途徑，以及通過研究圖形不斷的提高圖形研究意識、形成圖形研究能力，提升數學素養。